Practice SL 3.6—Voronoi diagrams with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
A Voronoi diagram of four fast-food restaurants, , , , and , is shown. A new customer appears at point .
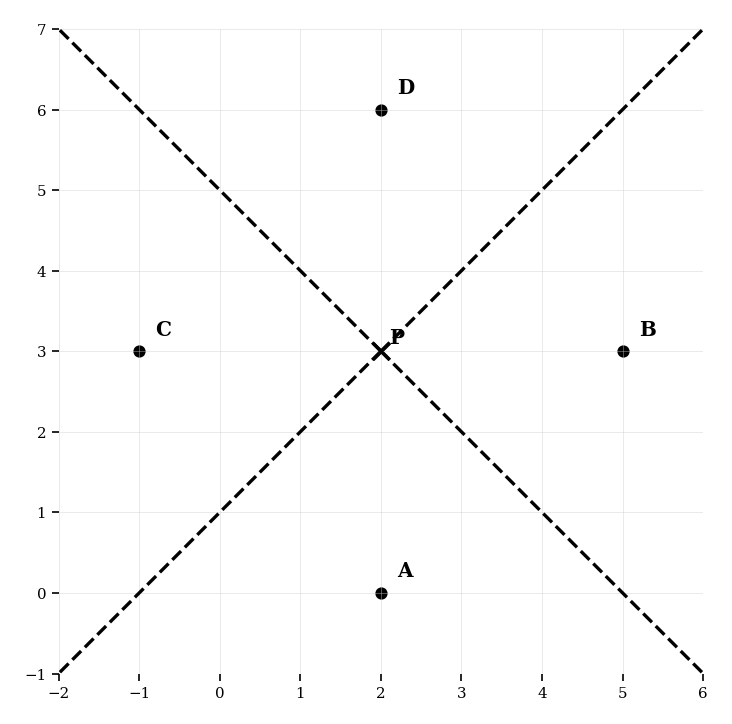
List all restaurants that are equally closest to point .
If restaurant is moved from to , how does this affect the Voronoi region?
Four schools are located at the vertices of a square: , , , and . A fifth school, , is to be added so that its Voronoi region shares boundaries with all four existing regions.
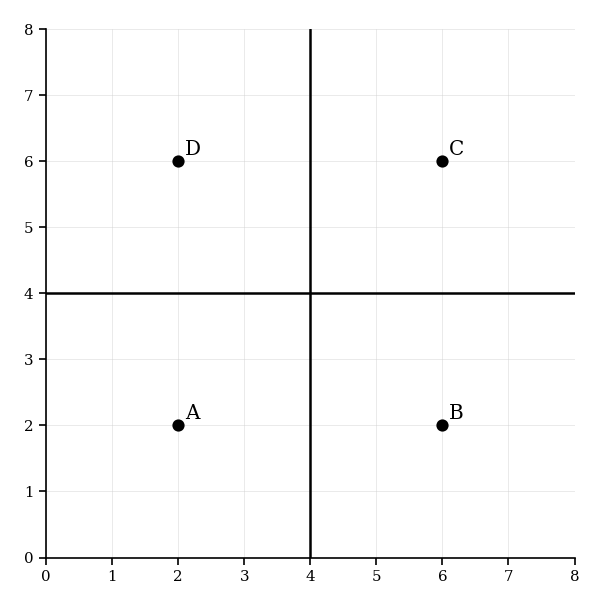
Explain the geometric condition required for this to occur.
Give a set of coordinates for the fifth school and justify why it satisfies the condition.
Sketch the updated Voronoi diagram.
A Voronoi diagram is constructed using the sites , , and , as shown in the diagram below.
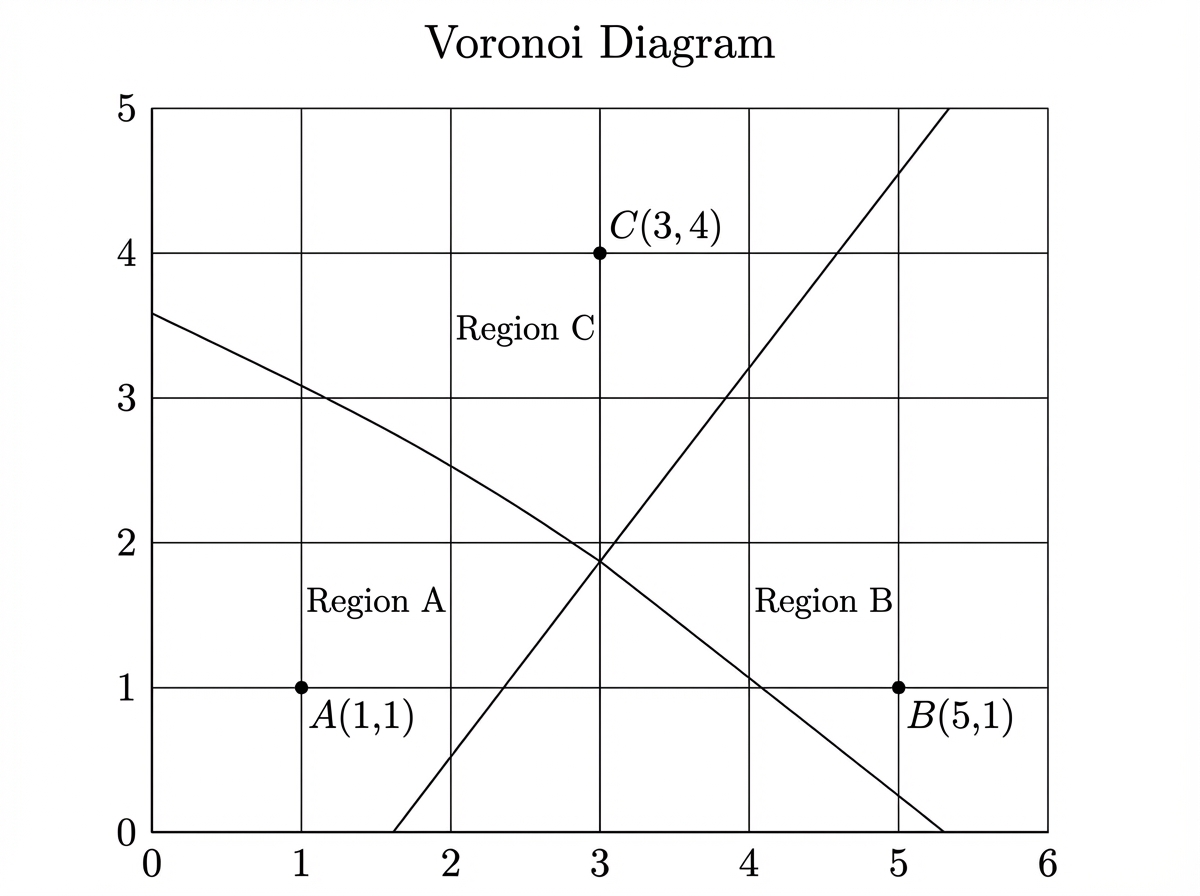
A new point is added to the diagram.
Sketch the modified Voronoi diagram including point .
Describe how the region of point will change.
A city has three hospitals located at points , and . A Voronoi diagram is created to determine which areas are closest to each hospital.
Plot the hospitals and sketch a rough Voronoi diagram.
A person at point needs medical attention. Which hospital should they go to?
A cell tower company is placing three towers at , , and . A customer is located at point .
Construct a Voronoi diagram for the tower locations.
Determine which tower the customer connects to.
Justify your answer using distance calculations.
The diagram below shows a Voronoi diagram formed by five points: , , , , and . Each region corresponds to the area closest to one of the points.
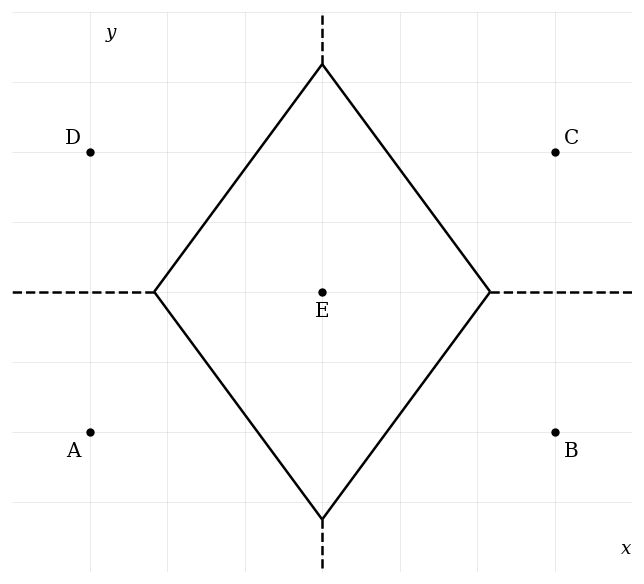
Which region corresponds to point ?
Find the equation of the perpendicular bisector used to separate the regions of and .
The Voronoi diagram below shows regions around delivery centers , , and . Point lies within the region of .
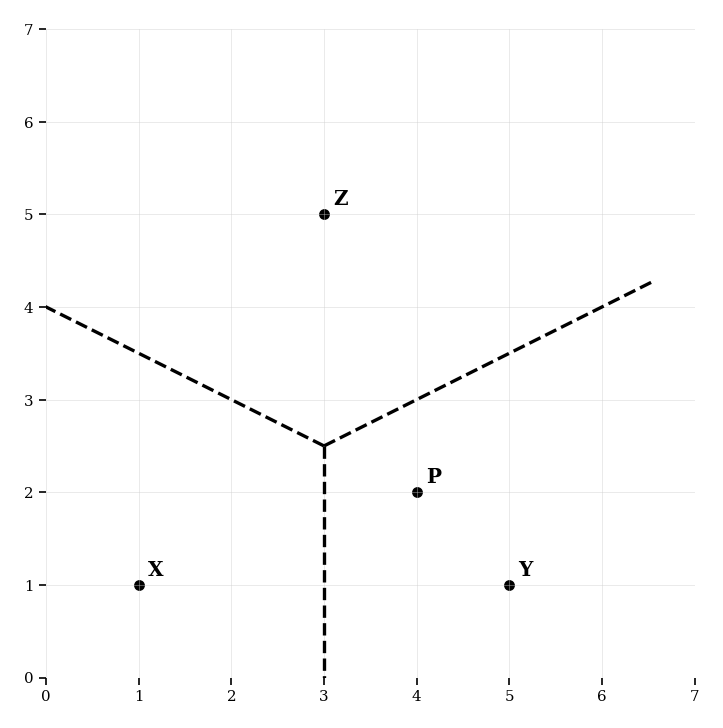
Verify that is closer to than to or .
Consider points and . A region is defined as all points that are closer to than to and lie within the circle .
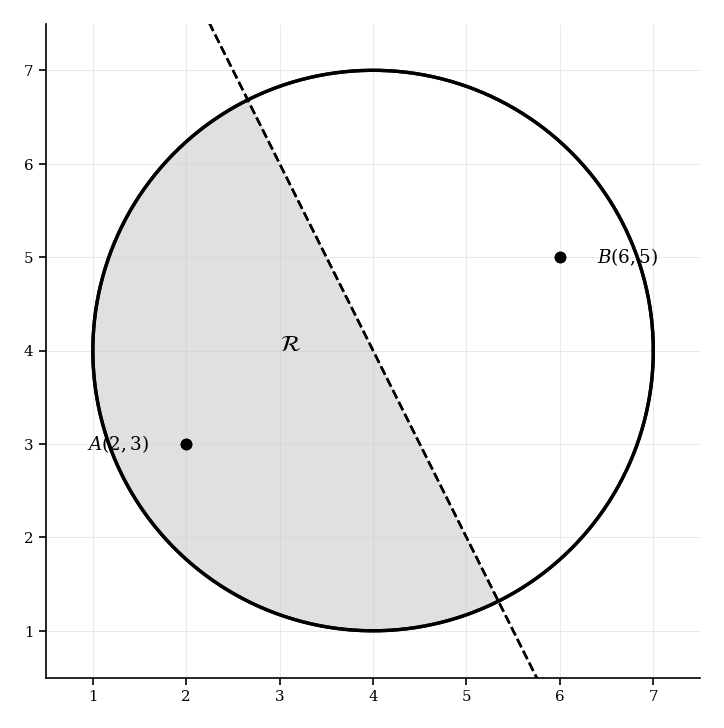
Find the equation of the perpendicular bisector of .
Determine the inequality that defines the half-plane of (closer to ).
Determine the area of region using integration or geometry.
A Voronoi diagram is created using four shops located at , , , and . The shops are located within a square town bounded by and .
Without plotting, explain why the region for is bounded.
Suggest coordinates for a point that would fall within the region of .
Add a new shop at so that it reduces the region of significantly. State possible coordinates and justify your choice.
Six restaurant locations (labelled A, B, C, D, E and F) are shown, together with their Voronoi diagram. All distances are measured in kilometres. 
Elena wants to eat at the closest restaurant to her. Write down the restaurant she should go to, if she is at (2,7).
Elena wants to eat at the closest restaurant to her. Write down the restaurant she should go to, if she is at (0,1), when restaurant A is closed.
Find the equation of the perpendicular bisector of CD.
Find the equation of the perpendicular bisector of BC.
Hence find the coordinates of the point which is of equal distance from B, C and D.
Hence find the distance of this point from D.
Practice SL 3.6—Voronoi diagrams with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
A Voronoi diagram of four fast-food restaurants, , , , and , is shown. A new customer appears at point .

List all restaurants that are equally closest to point .
If restaurant is moved from to , how does this affect the Voronoi region?
Four schools are located at the vertices of a square: , , , and . A fifth school, , is to be added so that its Voronoi region shares boundaries with all four existing regions.

Explain the geometric condition required for this to occur.
Give a set of coordinates for the fifth school and justify why it satisfies the condition.
Sketch the updated Voronoi diagram.
A Voronoi diagram is constructed using the sites , , and , as shown in the diagram below.

A new point is added to the diagram.
Sketch the modified Voronoi diagram including point .
Describe how the region of point will change.
A city has three hospitals located at points , and . A Voronoi diagram is created to determine which areas are closest to each hospital.
Plot the hospitals and sketch a rough Voronoi diagram.
A person at point needs medical attention. Which hospital should they go to?
A cell tower company is placing three towers at , , and . A customer is located at point .
Construct a Voronoi diagram for the tower locations.
Determine which tower the customer connects to.
Justify your answer using distance calculations.
The diagram below shows a Voronoi diagram formed by five points: , , , , and . Each region corresponds to the area closest to one of the points.

Which region corresponds to point ?
Find the equation of the perpendicular bisector used to separate the regions of and .
The Voronoi diagram below shows regions around delivery centers , , and . Point lies within the region of .

Verify that is closer to than to or .
Consider points and . A region is defined as all points that are closer to than to and lie within the circle .

Find the equation of the perpendicular bisector of .
Determine the inequality that defines the half-plane of (closer to ).
Determine the area of region using integration or geometry.
A Voronoi diagram is created using four shops located at , , , and . The shops are located within a square town bounded by and .
Without plotting, explain why the region for is bounded.
Suggest coordinates for a point that would fall within the region of .
Add a new shop at so that it reduces the region of significantly. State possible coordinates and justify your choice.
Six restaurant locations (labelled A, B, C, D, E and F) are shown, together with their Voronoi diagram. All distances are measured in kilometres. 
Elena wants to eat at the closest restaurant to her. Write down the restaurant she should go to, if she is at (2,7).
Elena wants to eat at the closest restaurant to her. Write down the restaurant she should go to, if she is at (0,1), when restaurant A is closed.
Find the equation of the perpendicular bisector of CD.
Find the equation of the perpendicular bisector of BC.
Hence find the coordinates of the point which is of equal distance from B, C and D.
Hence find the distance of this point from D.