Practice Statistics and Probability with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
A network of paths connects four nodes, A, B, C, and D, as shown:
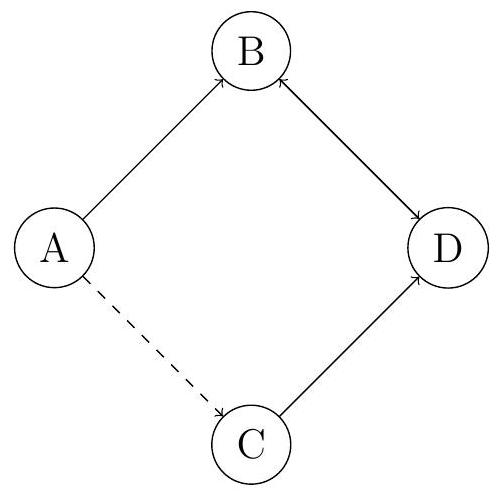
Dashed lines indicate paths that are twice as likely to be chosen.
Construct the transition matrix for a particle moving between the nodes.
Find the steady-state probability distribution using a graphic display calculator.
Explain one limitation of this model in the context of path selection.
A quality control officer tests the resistance (in ohms) of resistors produced in a factory, which follows a normal distribution with mean 100 ohms and variance 16 ohms . A sample of 12 resistors is taken, with ohms and ohms .
Calculate an unbiased estimate for the population variance.
Construct a confidence interval for the population mean resistance, using the sample standard deviation.
The factory claims the mean resistance is 98 ohms. Comment on the validity of this claim using the confidence interval.
If the total resistance of three resistors is measured, find the probability that it exceeds 305 ohms.
A call center receives an average of 5 calls per hour. The number of calls received follows a Poisson distribution.
Calculate the probability that the call center receives exactly 3 calls in a given hour.
Find the probability that the call center receives more than 7 calls in a given hour.
The time taken to process an online order at a warehouse follows a normal distribution with a mean of 12 minutes and a standard deviation of 3 minutes. A sample of 25 orders is randomly selected.
State the distribution of the sample mean, including its mean and standard deviation.
Find the probability that the sample mean processing time is more than 13 minutes.
Determine the value such that there is a probability that the sample mean lies within minutes of the population mean.
Consider two events and such that , , and .
Calculate .
Find .
A system transitions between states , and with transition matrix:
Find an eigenvector corresponding to the eigenvalue .
Using Part 1, determine the long-term probability of being in state .
A random variable is normally distributed with mean and variance . A linear transformation is defined as , where and are independent observations of .
Find the expected value of .
Calculate the variance of .
Find the probability that is between and .
Sketch the distribution of , shading the region where .
Show that the estimator is unbiased for the mean of .
A factory produces batteries with a claimed mean lifespan of 200 hours and a standard deviation of 20 hours. A sample of 50 batteries is tested at the significance level to see if the mean lifespan is less than 200 hours.
State the hypotheses and find the critical region.
If the sample mean is 195 hours, calculate the -value and state the conclusion.
If the true mean is 190 hours, find the probability of a Type II error.
Hank sets up a bird table in his garden to provide the local birds with some food. Hank notices that a specific bird, a large magpie, visits several times per month and he names him Bill. Hank models the number of times per month that Bill visits his garden as a Poisson distribution with mean 3.1.
Using Hank's model, find the probability that Bill visits the garden on exactly four occasions during one particular month.
Over the course of 3 consecutive months, find the probability that Bill visits the garden on exactly 12 occasions.
Over the course of 3 consecutive months, find the probability that Bill visits the garden during the first and third month only.
Find the probability that over a 12-month period, there will be exactly 3 months when Bill does not visit the garden.
After the first year, a number of baby magpies start to visit Hank's garden. It may be assumed that each of these baby magpies visits the garden randomly and independently, and that the number of times each baby magpie visits the garden per month is modelled by a Poisson distribution with mean 2.1.
Determine the least number of magpies required, including Bill, in order that the probability of Hank's garden having at least 30 magpie visits per month is greater than 0.2.
A zoo has three habitats, H, I, and J, connected as shown in the diagram below:
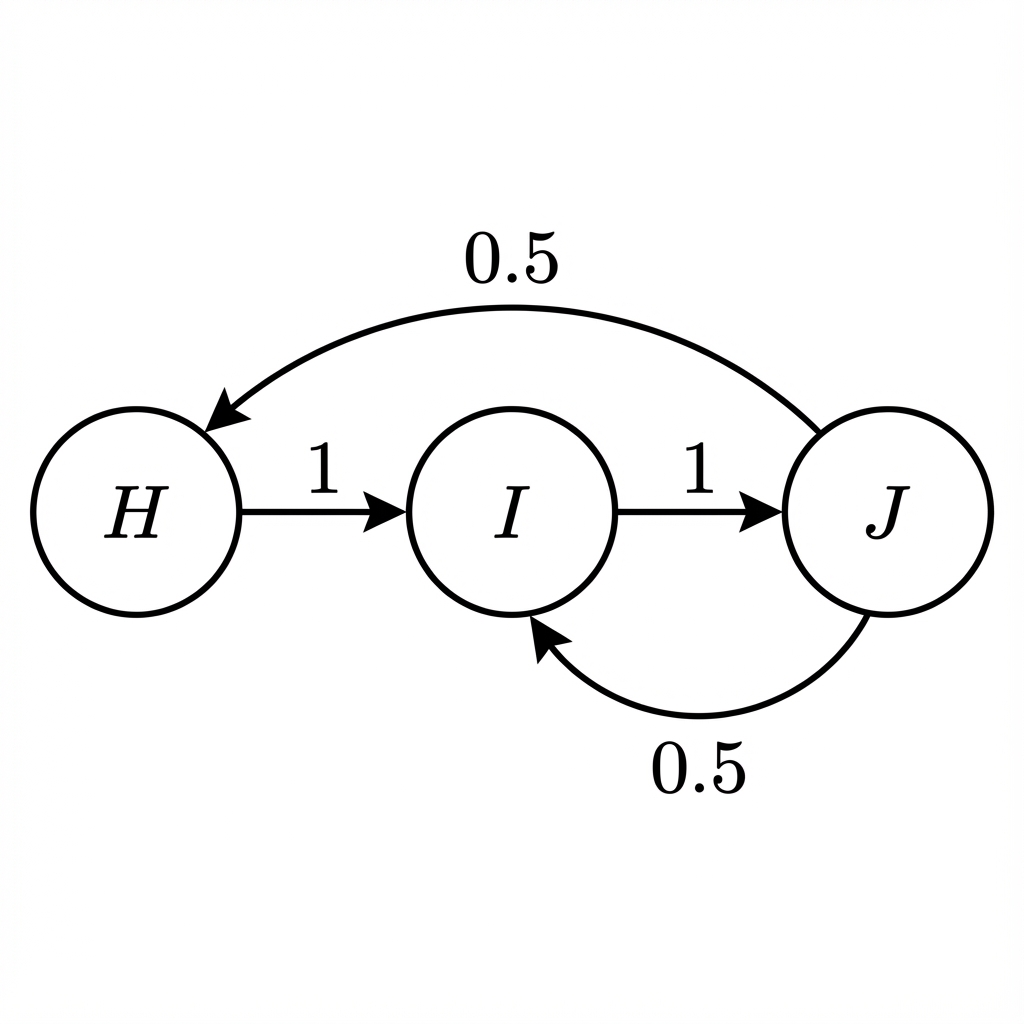
An animal moves between habitats with equal probability for each available path from its current habitat.
Write down the transition matrix, , for this system.
If the animal starts in habitat H, find the probability it is in habitat J after two moves.
Find the long-term probability of the animal being in habitat I.
Practice Statistics and Probability with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
A network of paths connects four nodes, A, B, C, and D, as shown:

Dashed lines indicate paths that are twice as likely to be chosen.
Construct the transition matrix for a particle moving between the nodes.
Find the steady-state probability distribution using a graphic display calculator.
Explain one limitation of this model in the context of path selection.
A quality control officer tests the resistance (in ohms) of resistors produced in a factory, which follows a normal distribution with mean 100 ohms and variance 16 ohms . A sample of 12 resistors is taken, with ohms and ohms .
Calculate an unbiased estimate for the population variance.
Construct a confidence interval for the population mean resistance, using the sample standard deviation.
The factory claims the mean resistance is 98 ohms. Comment on the validity of this claim using the confidence interval.
If the total resistance of three resistors is measured, find the probability that it exceeds 305 ohms.
A call center receives an average of 5 calls per hour. The number of calls received follows a Poisson distribution.
Calculate the probability that the call center receives exactly 3 calls in a given hour.
Find the probability that the call center receives more than 7 calls in a given hour.
The time taken to process an online order at a warehouse follows a normal distribution with a mean of 12 minutes and a standard deviation of 3 minutes. A sample of 25 orders is randomly selected.
State the distribution of the sample mean, including its mean and standard deviation.
Find the probability that the sample mean processing time is more than 13 minutes.
Determine the value such that there is a probability that the sample mean lies within minutes of the population mean.
Consider two events and such that , , and .
Calculate .
Find .
A system transitions between states , and with transition matrix:
Find an eigenvector corresponding to the eigenvalue .
Using Part 1, determine the long-term probability of being in state .
A random variable is normally distributed with mean and variance . A linear transformation is defined as , where and are independent observations of .
Find the expected value of .
Calculate the variance of .
Find the probability that is between and .
Sketch the distribution of , shading the region where .
Show that the estimator is unbiased for the mean of .
A factory produces batteries with a claimed mean lifespan of 200 hours and a standard deviation of 20 hours. A sample of 50 batteries is tested at the significance level to see if the mean lifespan is less than 200 hours.
State the hypotheses and find the critical region.
If the sample mean is 195 hours, calculate the -value and state the conclusion.
If the true mean is 190 hours, find the probability of a Type II error.
Hank sets up a bird table in his garden to provide the local birds with some food. Hank notices that a specific bird, a large magpie, visits several times per month and he names him Bill. Hank models the number of times per month that Bill visits his garden as a Poisson distribution with mean 3.1.
Using Hank's model, find the probability that Bill visits the garden on exactly four occasions during one particular month.
Over the course of 3 consecutive months, find the probability that Bill visits the garden on exactly 12 occasions.
Over the course of 3 consecutive months, find the probability that Bill visits the garden during the first and third month only.
Find the probability that over a 12-month period, there will be exactly 3 months when Bill does not visit the garden.
After the first year, a number of baby magpies start to visit Hank's garden. It may be assumed that each of these baby magpies visits the garden randomly and independently, and that the number of times each baby magpie visits the garden per month is modelled by a Poisson distribution with mean 2.1.
Determine the least number of magpies required, including Bill, in order that the probability of Hank's garden having at least 30 magpie visits per month is greater than 0.2.
A zoo has three habitats, H, I, and J, connected as shown in the diagram below:

An animal moves between habitats with equal probability for each available path from its current habitat.
Write down the transition matrix, , for this system.
If the animal starts in habitat H, find the probability it is in habitat J after two moves.
Find the long-term probability of the animal being in habitat I.