Practice AHL 3.15—Adjacency matrices and tables with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
A transport network has hubs , and , with directed edges representing one-way routes. The adjacency matrix includes self-loops (hubs retaining cargo):
Draw the directed graph, including self-loops.
Find the number of walks of length 5 from to .
A cargo starts at . Determine which hubs are reached after exactly 4 steps.
A new hub is added, sending to and , and receiving from . Update the adjacency matrix and graph.
In the updated network, find the number of walks of length 3 from to , and interpret in the context of cargo transport.
A city's metro system has stations , with weighted edges representing distances (in km). The adjacency matrix is:
Construct the adjacency table for the network.
Use Kruskal's algorithm to find the MST, listing edges in order of selection.
A tourist starts at and visits all stations, returning to . Use the nearest neighbor algorithm to find an upper bound for the distance.
Find a lower bound using the MST from part (b).
If a new station is added with edges , and , update the MST and calculate its new total weight.
A neural network has nodes , and , with directed edges representing signal propagation. The adjacency matrix is given by:
Draw the directed graph representing this neural network.
Find the number of walks of length 6 from to .
List all trails of length 4 from to .
A new node is added. It sends signals to and , and receives signals from . Update the adjacency matrix and draw the updated graph.
In the updated network, find the number of nodes reachable from in exactly 3 steps.
A museum has exhibits , and , connected by pathways with weights representing viewing times (in minutes). The adjacency matrix for the museum is given by:
Construct the adjacency table for the pathways and their respective viewing times.
Use Kruskal's algorithm to find the minimum spanning tree (MST) for the network, listing the edges in the order they are selected.
A visitor wants to view all exhibits, starting and ending at . Find an upper bound for the total travel time using the nearest neighbor algorithm.
Find a lower bound for the travel time by deleting vertex and using the MST found in part 2.
If a new exhibit is added with pathways , and , update the MST and calculate its total weight.
Based on the graph:
Create the complete weighted adjacency matrix (including the shortest weighted connection between every two vertices).
Find the upper bound for the travelling salesman problem using vertex A.
Based on this graph:
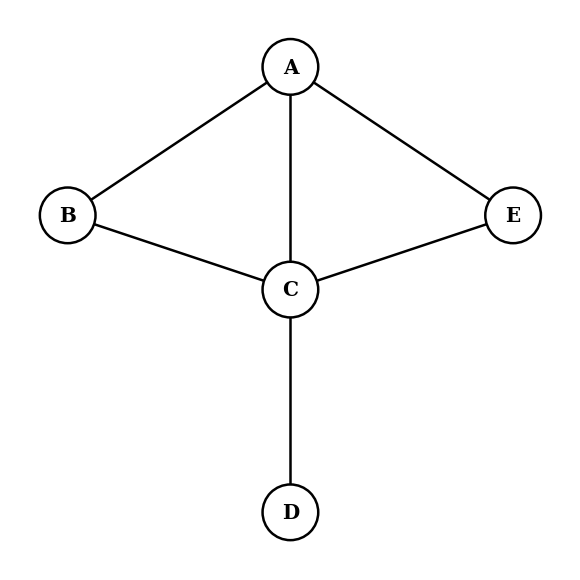
Write down the adjacency matrix for this graph.
Find a Hamiltonian path in this graph.
State the change that would be needed for a Hamiltonian cycle to be present.
Based on the graph:
Create an unweighted adjacency matrix for the graph.
Hence, identify the odd vertices.
Hence, find the solution to the Chinese Postman Problem.
Based on the graph:
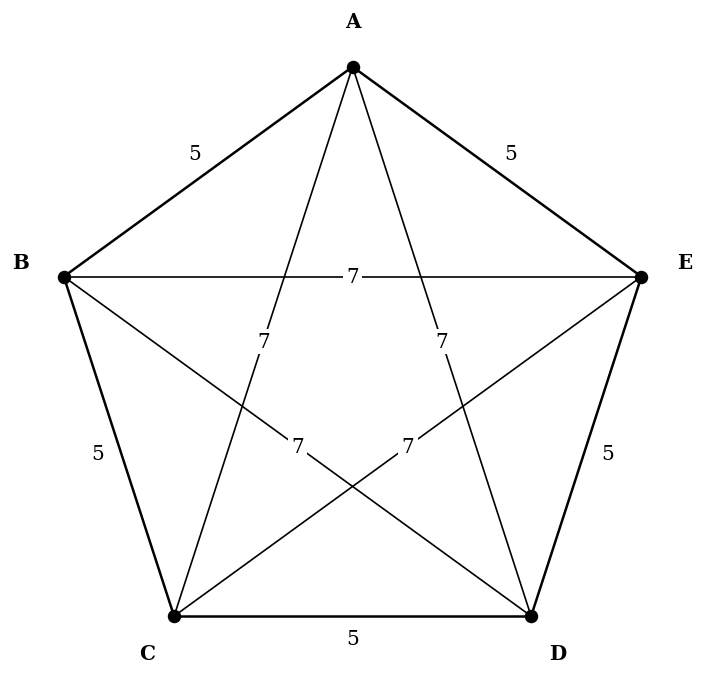
Create the weighted adjacency matrix showing all shortest connections.
Use the deleted vertex theorem with each vertex to find the best lower bound.
Use the nearest neighbour algorithm to find the upper bound.
Hence or otherwise, solve the travelling salesman problem.
A robot navigates a grid of six rooms, , and . The possible movements between rooms are represented by a directed graph. Some paths are marked with sensors (indicated by dashed edges); these paths have twice the probability of being chosen compared to normal paths from the same room.
The movements are shown in the following graph:
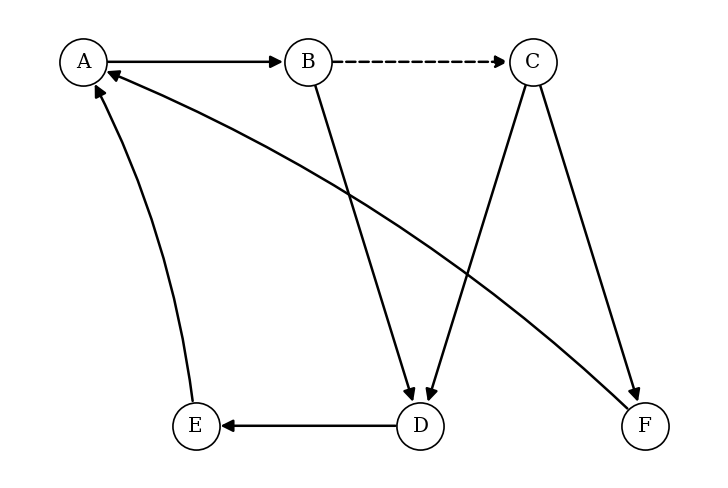
Note: For vertex , the path to is a sensor path, while the path to is a normal path. For vertex , both paths to and are normal paths. All other vertices have a single outgoing normal path as shown.
Determine the transition matrix, , for the robot's movement.
Using a graphic display calculator, estimate the percentage of time the robot spends at room if it moves indefinitely.
Comment on one limitation of this probabilistic model in representing a real robot's movement.
A new room is added to the system. The path from is changed to a normal path to , and a new sensor path is added from to . Update the transition matrix to represent this new 7-room system.
Based on this graph:
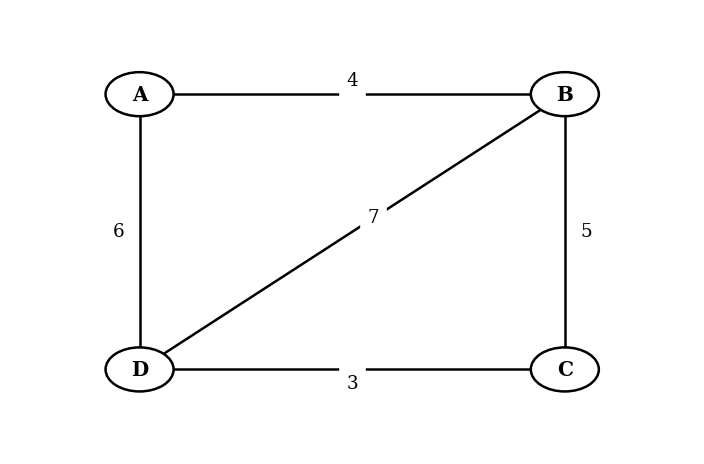
Create a weighted adjacency matrix for the graph, with vertices listed in alphabetical order (A, B, C, D).
Use Kruskal's algorithm to find the minimum spanning tree, stating the order in which edges are added and the total weight of the tree.
Practice AHL 3.15—Adjacency matrices and tables with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
A transport network has hubs , and , with directed edges representing one-way routes. The adjacency matrix includes self-loops (hubs retaining cargo):
Draw the directed graph, including self-loops.
Find the number of walks of length 5 from to .
A cargo starts at . Determine which hubs are reached after exactly 4 steps.
A new hub is added, sending to and , and receiving from . Update the adjacency matrix and graph.
In the updated network, find the number of walks of length 3 from to , and interpret in the context of cargo transport.
A city's metro system has stations , with weighted edges representing distances (in km). The adjacency matrix is:
Construct the adjacency table for the network.
Use Kruskal's algorithm to find the MST, listing edges in order of selection.
A tourist starts at and visits all stations, returning to . Use the nearest neighbor algorithm to find an upper bound for the distance.
Find a lower bound using the MST from part (b).
If a new station is added with edges , and , update the MST and calculate its new total weight.
A neural network has nodes , and , with directed edges representing signal propagation. The adjacency matrix is given by:
Draw the directed graph representing this neural network.
Find the number of walks of length 6 from to .
List all trails of length 4 from to .
A new node is added. It sends signals to and , and receives signals from . Update the adjacency matrix and draw the updated graph.
In the updated network, find the number of nodes reachable from in exactly 3 steps.
A museum has exhibits , and , connected by pathways with weights representing viewing times (in minutes). The adjacency matrix for the museum is given by:
Construct the adjacency table for the pathways and their respective viewing times.
Use Kruskal's algorithm to find the minimum spanning tree (MST) for the network, listing the edges in the order they are selected.
A visitor wants to view all exhibits, starting and ending at . Find an upper bound for the total travel time using the nearest neighbor algorithm.
Find a lower bound for the travel time by deleting vertex and using the MST found in part 2.
If a new exhibit is added with pathways , and , update the MST and calculate its total weight.
Based on the graph:
Create the complete weighted adjacency matrix (including the shortest weighted connection between every two vertices).
Find the upper bound for the travelling salesman problem using vertex A.
Based on this graph:

Write down the adjacency matrix for this graph.
Find a Hamiltonian path in this graph.
State the change that would be needed for a Hamiltonian cycle to be present.
Based on the graph:
Create an unweighted adjacency matrix for the graph.
Hence, identify the odd vertices.
Hence, find the solution to the Chinese Postman Problem.
Based on the graph:

Create the weighted adjacency matrix showing all shortest connections.
Use the deleted vertex theorem with each vertex to find the best lower bound.
Use the nearest neighbour algorithm to find the upper bound.
Hence or otherwise, solve the travelling salesman problem.
A robot navigates a grid of six rooms, , and . The possible movements between rooms are represented by a directed graph. Some paths are marked with sensors (indicated by dashed edges); these paths have twice the probability of being chosen compared to normal paths from the same room.
The movements are shown in the following graph:

Note: For vertex , the path to is a sensor path, while the path to is a normal path. For vertex , both paths to and are normal paths. All other vertices have a single outgoing normal path as shown.
Determine the transition matrix, , for the robot's movement.
Using a graphic display calculator, estimate the percentage of time the robot spends at room if it moves indefinitely.
Comment on one limitation of this probabilistic model in representing a real robot's movement.
A new room is added to the system. The path from is changed to a normal path to , and a new sensor path is added from to . Update the transition matrix to represent this new 7-room system.
Based on this graph:

Create a weighted adjacency matrix for the graph, with vertices listed in alphabetical order (A, B, C, D).
Use Kruskal's algorithm to find the minimum spanning tree, stating the order in which edges are added and the total weight of the tree.