Practice SL 3.1—3d space, volume, angles, midpoints with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
An architect is designing a right pyramid with a square base for a new monument. The base has a side length of 10 cm, and the height from the base to the apex is 12 cm.
Calculate the area of the square base.
Using your answer from part (a), determine the volume of the pyramid.
Calculate the slant height of the pyramid, which is the distance from the midpoint of a base edge to the apex.
Find the total surface area of the pyramid, including the base and all triangular faces.
A hot air balloon is directly above a point on the ground that lies on the line segment connecting two observers, A and B, who are standing 100 meters apart. The angle of elevation from observer A to the balloon is , and the angle of elevation from observer B is .
Draw a labeled diagram representing the situation, showing the positions of the balloon, observers, and angles of elevation.
Calculate the height of the balloon above the ground based on the observations from points A and B.
A factory packages coconut water in cone-shaped containers with a base radius of 5.2 cm and a height of 13 cm.
The factory designers are currently investigating whether a cone-shaped container can be replaced with a cylinder-shaped container with the same radius and the same total surface area.
Find the slant height of the cone-shaped container.
Show that the total surface area of the cone-shaped container is 314 cm2, correct to three significant figures.
Find the height, $h$, of this cylinder-shaped container.
The factory director wants to increase the volume of coconut water sold per container.
State whether or not they should replace the cone-shaped containers with cylinder‑shaped containers. Justify your conclusion.
Iron in the asteroid 16 Psyche is said to be valued at $8973$ quadrillion euros (EUR), where one quadrillion $= 10^{15}$.
James believes the asteroid is approximately spherical with radius $113 \text{ km}$. He uses this information to estimate its volume.
Write down the value of the iron in the form $a \times 10^k$ where $1 \le a < 10, k \in \mathbb{Z}$.
Calculate James’s estimate of its volume, in $\text{km}^3$.
The actual volume of the asteroid is found to be $6.074 \times 10^6 \text{ km}^3$.
Find the percentage error in James’s estimate of the volume.
Joey is making a party hat in the form of a cone. The hat is made from a sector, , of a circular piece of paper with a radius of and as shown in the diagram.
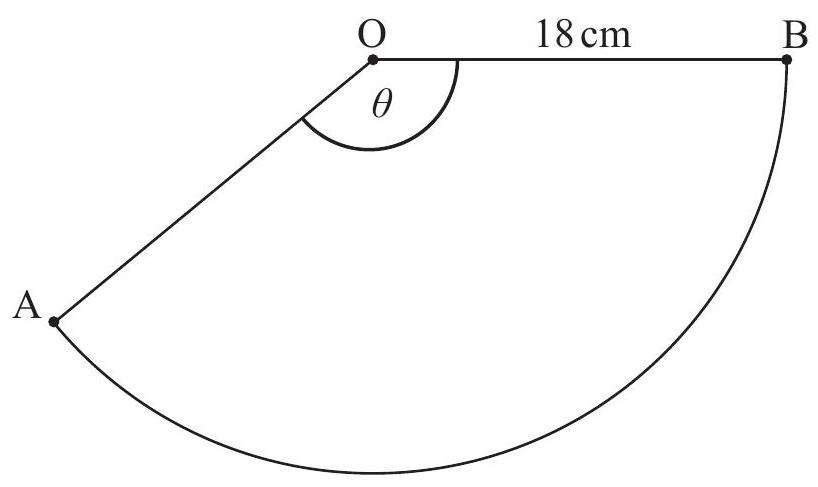
To make the hat, sides and are joined together. The hat has a base radius of .
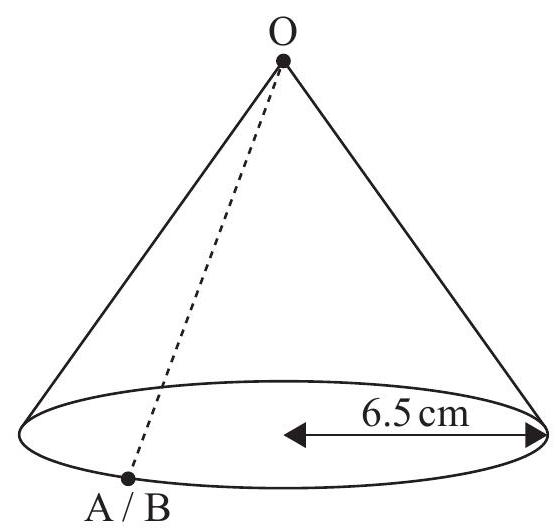
Write down the perimeter of the base of the hat in terms of .
Find the value of .
Find the surface area of the outside of the hat.
A civil engineer is studying the intersection of two pathways in a park, represented by the direction vectors and .
Calculate the angle between these pathways.
Determine the angle between the plane defined by the equation and the line described by the parametric equations . Explain what this angle indicates about the position of the line relative to the plane.
A balloon in the shape of a sphere is filled with helium until the radius is 6 cm.
Calculate the volume of the balloon.
The volume of the balloon is increased by 40%. Calculate the radius of the balloon following this increase.
A cylindrical water tank with a radius of 5 cm and a height of 12 cm is topped with a cone of the same radius and a height of 9 cm.
Calculate the total volume of the combined shape, which represents the maximum capacity of the tank.
Determine the total surface area of the combined shape, including the base of the tank and the cone, to understand the material required for manufacturing.
A submarine is located in a sea at coordinates $(0.8, 1.3, -0.3)$ relative to a ship positioned at the origin $O$. The $x$ direction is due east, the $y$ direction is due north and the $z$ direction is vertically upwards.
All distances are measured in kilometres.
The submarine travels with direction vector $\begin{pmatrix} -2 \\ -3 \\ 1 \end{pmatrix}$.
The submarine reaches the surface of the sea at the point $P$.
Assuming the submarine travels in a straight line, write down an equation for the line along which it travels.
Find the coordinates of $P$.
Find $OP$.
Intersection of three planes
Find the coordinates of the point of intersection of the planes defined by the equations , and .
Practice SL 3.1—3d space, volume, angles, midpoints with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
An architect is designing a right pyramid with a square base for a new monument. The base has a side length of 10 cm, and the height from the base to the apex is 12 cm.
Calculate the area of the square base.
Using your answer from part (a), determine the volume of the pyramid.
Calculate the slant height of the pyramid, which is the distance from the midpoint of a base edge to the apex.
Find the total surface area of the pyramid, including the base and all triangular faces.
A hot air balloon is directly above a point on the ground that lies on the line segment connecting two observers, A and B, who are standing 100 meters apart. The angle of elevation from observer A to the balloon is , and the angle of elevation from observer B is .
Draw a labeled diagram representing the situation, showing the positions of the balloon, observers, and angles of elevation.
Calculate the height of the balloon above the ground based on the observations from points A and B.
A factory packages coconut water in cone-shaped containers with a base radius of 5.2 cm and a height of 13 cm.
The factory designers are currently investigating whether a cone-shaped container can be replaced with a cylinder-shaped container with the same radius and the same total surface area.
Find the slant height of the cone-shaped container.
Show that the total surface area of the cone-shaped container is 314 cm2, correct to three significant figures.
Find the height, $h$, of this cylinder-shaped container.
The factory director wants to increase the volume of coconut water sold per container.
State whether or not they should replace the cone-shaped containers with cylinder‑shaped containers. Justify your conclusion.
Iron in the asteroid 16 Psyche is said to be valued at $8973$ quadrillion euros (EUR), where one quadrillion $= 10^{15}$.
James believes the asteroid is approximately spherical with radius $113 \text{ km}$. He uses this information to estimate its volume.
Write down the value of the iron in the form $a \times 10^k$ where $1 \le a < 10, k \in \mathbb{Z}$.
Calculate James’s estimate of its volume, in $\text{km}^3$.
The actual volume of the asteroid is found to be $6.074 \times 10^6 \text{ km}^3$.
Find the percentage error in James’s estimate of the volume.
Joey is making a party hat in the form of a cone. The hat is made from a sector, , of a circular piece of paper with a radius of and as shown in the diagram.

To make the hat, sides and are joined together. The hat has a base radius of .

Write down the perimeter of the base of the hat in terms of .
Find the value of .
Find the surface area of the outside of the hat.
A civil engineer is studying the intersection of two pathways in a park, represented by the direction vectors and .
Calculate the angle between these pathways.
Determine the angle between the plane defined by the equation and the line described by the parametric equations . Explain what this angle indicates about the position of the line relative to the plane.
A balloon in the shape of a sphere is filled with helium until the radius is 6 cm.
Calculate the volume of the balloon.
The volume of the balloon is increased by 40%. Calculate the radius of the balloon following this increase.
A cylindrical water tank with a radius of 5 cm and a height of 12 cm is topped with a cone of the same radius and a height of 9 cm.
Calculate the total volume of the combined shape, which represents the maximum capacity of the tank.
Determine the total surface area of the combined shape, including the base of the tank and the cone, to understand the material required for manufacturing.
A submarine is located in a sea at coordinates $(0.8, 1.3, -0.3)$ relative to a ship positioned at the origin $O$. The $x$ direction is due east, the $y$ direction is due north and the $z$ direction is vertically upwards.
All distances are measured in kilometres.
The submarine travels with direction vector $\begin{pmatrix} -2 \\ -3 \\ 1 \end{pmatrix}$.
The submarine reaches the surface of the sea at the point $P$.
Assuming the submarine travels in a straight line, write down an equation for the line along which it travels.
Find the coordinates of $P$.
Find $OP$.
Intersection of three planes
Find the coordinates of the point of intersection of the planes defined by the equations , and .