Practice SL 3.2—2d and 3d trig with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
A builder is assessing a triangular support structure with side lengths cm, cm, and cm to ensure it meets right-angle specifications.
Prove that △ABC is a right-angled triangle, verifying the relationship between the sides.
Calculate the area of △ABC to determine the space it occupies.
A builder is using a right-angled triangular support structure with sides , , and , where is the angle opposite side .
Find the values of , , and to understand the structural angles.
Use the Pythagorean theorem to verify the relationship between the sides, confirming the triangle’s right-angle properties.
The lengths of two of the sides in a triangle are cm and cm. Let be the angle between the two given sides. The triangle has an area of cm.
Show that .
Find the two possible values for the length of the third side.
The diagram represents a right-angled triangular support structure △ABC, where . This structure is designed to support a construction scaffold at angle A from the horizontal.
In the right triangle shown, prove that by using the Pythagorean theorem to find the missing side length.
Calculate the value of using the double angle formula, which may be used to analyze forces on the scaffold.
Determine the length of the hypotenuse if the opposite side to A is scaled up to 15 meters, keeping the triangle’s proportions constant.
A triangular garden plot has two known sides, and , with an angle between them.
Calculate the length of side , which represents the boundary line opposite angle .
Calculate the area of to estimate the total area of the garden plot.
A triangular field ABC is such that AB = 56 m and BC = 82 m, each measured correct to the nearest metre, and the angle at B is equal to 105°, measured correct to the nearest 5°. 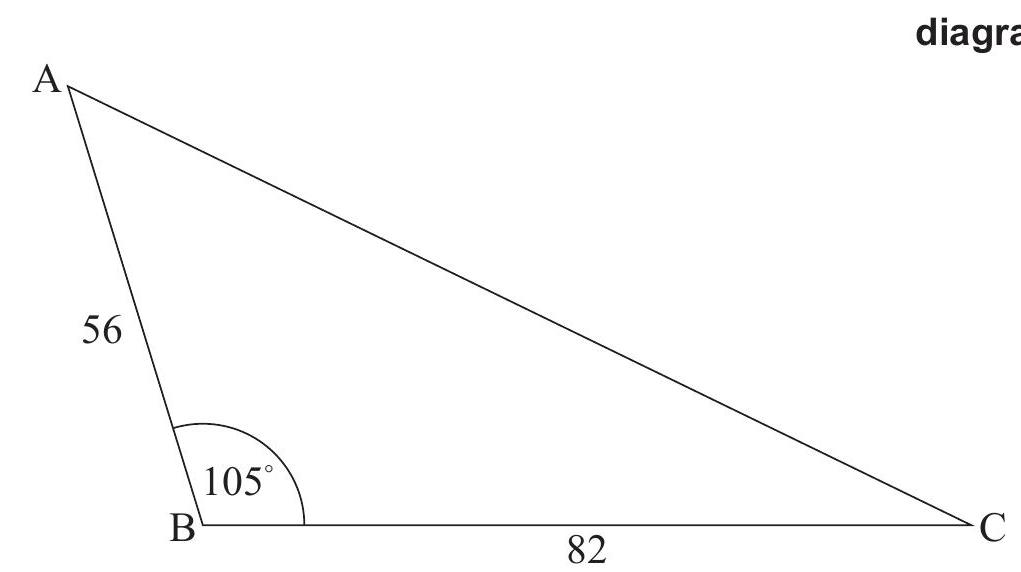
Calculate the maximum possible area of the field.
At $1{:}00 ext{ pm}$ a ship is $1 ext{ km}$ east and $4 ext{ km}$ north of a harbour. A coordinate system is defined with the harbour at the origin. The position vector of the ship at $1{:}00 ext{ pm}$ is given by $\begin{pmatrix} 1 \\ 4 \end{pmatrix}$.
The ship has a constant velocity of $\begin{pmatrix} 1.2 \\ -0.6 \end{pmatrix}$ kilometres per hour ($\text{km\,h}^{-1}$).
Write down an expression for the position vector $\mathbf{r}$ of the ship, $t$ hours after $1{:}00 ext{ pm}$.
Find the time at which the bearing of the ship from the harbour is $045^\circ$.
Two ships, A and B, leave a port, travelling in different directions. Ship A travels km on a bearing of , while ship B travels km on a bearing of .
Calculate the distance between the two ships after they complete their journeys.
A triangular garden plot has side lengths m, m, and an angle opposite side . The garden plot is known to be acute-angled.
Calculate the measure of angle using the sine rule to understand the dimensions of the garden.
Find the area of using the formula involving sine to estimate the garden’s planting area.
An architect is observing a building to determine its height. Standing 50 meters away from the base of the building, the architect looks up at the top of the building at an angle of elevation of .
Calculate the height of the building, based on the given distance and angle.
Practice SL 3.2—2d and 3d trig with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
A builder is assessing a triangular support structure with side lengths cm, cm, and cm to ensure it meets right-angle specifications.
Prove that △ABC is a right-angled triangle, verifying the relationship between the sides.
Calculate the area of △ABC to determine the space it occupies.
A builder is using a right-angled triangular support structure with sides , , and , where is the angle opposite side .
Find the values of , , and to understand the structural angles.
Use the Pythagorean theorem to verify the relationship between the sides, confirming the triangle’s right-angle properties.
The lengths of two of the sides in a triangle are cm and cm. Let be the angle between the two given sides. The triangle has an area of cm.
Show that .
Find the two possible values for the length of the third side.
The diagram represents a right-angled triangular support structure △ABC, where . This structure is designed to support a construction scaffold at angle A from the horizontal.
In the right triangle shown, prove that by using the Pythagorean theorem to find the missing side length.
Calculate the value of using the double angle formula, which may be used to analyze forces on the scaffold.
Determine the length of the hypotenuse if the opposite side to A is scaled up to 15 meters, keeping the triangle’s proportions constant.
A triangular garden plot has two known sides, and , with an angle between them.
Calculate the length of side , which represents the boundary line opposite angle .
Calculate the area of to estimate the total area of the garden plot.
A triangular field ABC is such that AB = 56 m and BC = 82 m, each measured correct to the nearest metre, and the angle at B is equal to 105°, measured correct to the nearest 5°. 
Calculate the maximum possible area of the field.
At $1{:}00 ext{ pm}$ a ship is $1 ext{ km}$ east and $4 ext{ km}$ north of a harbour. A coordinate system is defined with the harbour at the origin. The position vector of the ship at $1{:}00 ext{ pm}$ is given by $\begin{pmatrix} 1 \\ 4 \end{pmatrix}$.
The ship has a constant velocity of $\begin{pmatrix} 1.2 \\ -0.6 \end{pmatrix}$ kilometres per hour ($\text{km\,h}^{-1}$).
Write down an expression for the position vector $\mathbf{r}$ of the ship, $t$ hours after $1{:}00 ext{ pm}$.
Find the time at which the bearing of the ship from the harbour is $045^\circ$.
Two ships, A and B, leave a port, travelling in different directions. Ship A travels km on a bearing of , while ship B travels km on a bearing of .
Calculate the distance between the two ships after they complete their journeys.
A triangular garden plot has side lengths m, m, and an angle opposite side . The garden plot is known to be acute-angled.
Calculate the measure of angle using the sine rule to understand the dimensions of the garden.
Find the area of using the formula involving sine to estimate the garden’s planting area.
An architect is observing a building to determine its height. Standing 50 meters away from the base of the building, the architect looks up at the top of the building at an angle of elevation of .
Calculate the height of the building, based on the given distance and angle.