Practice Functions with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
The number of bacteria in a Petri dish is modelled by the function where is the number of bacteria and is the time in hours.
Write down the number of bacteria in the Petri dish at .
Calculate the number of bacteria present after 10 hours.
Calculate the time, in hours, for number of bacteria to reach 10000.
A hot winter soup has just been removed from the stove and is left outside to cool. The soup's temperature can be modelled by the function where is the time, in minutes, since the soup was removed from the stove. The temperature outside is .
Write down the value of a and explain why it has this value.
Initially the temperature of the soup is . Find the value of .
After two minutes, the temperature of the soup is . Find the value of .
After 15 minutes the soup is put into the fridge.
Calculate the temperature of the soup when it is put into the fridge.
The front view of the edge of a water tank is drawn on a set of axes below. The edge is modelled by
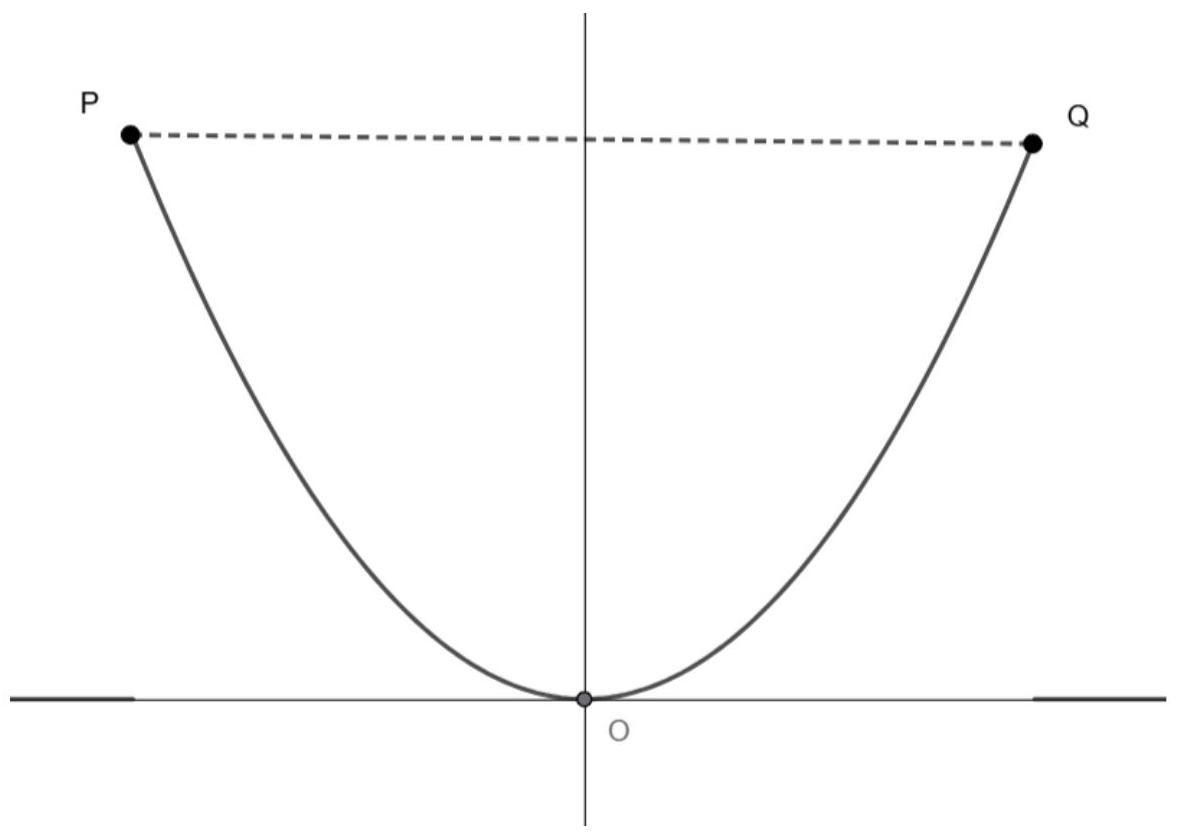
Point has coordinates , point has coordinates and point has coordinates .
Find the value of and of .
Hence, write down the equation of the quadratic function which models the edge of the water tank.
Given that 1 unit represents 1 m , find the width of the water tank when its height is 2.25 m .
The point lies on the curve . Write down the coordinates of the corresponding point under the following transformations.
The average temperature of a city, , in degrees Celsius, fluctuates throughout a year and can be modelled by the function where is the elapsed time, in weeks, since the start of the year. The average temperature of the city in week 4 is 27 degrees Celsius and in week 28 it is 12 degrees Celsius.
Find the value of , assuming there are 52 weeks in a year.
Write down two equations connecting and and find their values.
Calculate how many weeks of the year that they have to be careful about the food freezing. Give your answer to the nearest integer.
A particle moves along a straight line with displacement, , in meters, from a fixed point at time seconds, modeled by
for . The particle is at risk of collision when .
Find the initial displacement of the particle.
Write down the period of the oscillatory components.
Find the first time the particle is at risk of collision.
The velocity of the particle is . Find the maximum acceleration of the particle in the first 30 seconds, correct to three significant figures.
The following data represents the population of a certain species of fish in a lake over a period of 10 years. The population is believed to grow exponentially.
Construct a table showing the values of Year and , giving your answers correct to 3 decimal places.
| Year | Population |
|---|---|
| 1 | 150 |
| 2 | 220 |
| 3 | 320 |
| 4 | 470 |
| 5 | 680 |
| 6 | 980 |
| 7 | 1400 |
| 8 | 2000 |
| 9 | 2900 |
| 10 | 4200 |
Find the equation of the regression line of on Year.
In a biology lab, the population of a certain species of bacteria is observed to grow exponentially. The population in number of bacteria at time hours is modeled by the equation:
Find the initial population of the bacteria.
Determine the population after 10 hours.
Find the time required for the population to double.
A city planner is analyzing the linear function representing the cost of public transportation, given by
This function is transformed to produce a new function .
Write down the equation of if it represents reflected in the x-axis.
Write down the equation of if it represents reflected in the y-axis.
Describe the transformation applied to to obtain .
The point lies on the curve .
Find the coordinates of the corresponding point under .