Practice AHL 3.7—Radians with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
Convert radians to degrees.
Determine the value of .
Explain why angles measured in radians are dimensionless quantities.
A circle has a radius of 5 cm.
Express an angle of in radians.
Find the area of the sector subtended by the angle .
Determine the length of the arc subtended by the angle .
The lengths of two of the sides in a triangle are cm and cm. Let be the angle between the two given sides. The triangle has an area of cm.
Show that .
Find the two possible values for the length of the third side.
The figure shows sector OAB of a circle with centre O and radius cm. The angle subtended at the centre, , lies between . A perpendicular line is drawn from the point to meet the radius at the point , forming the right triangle .
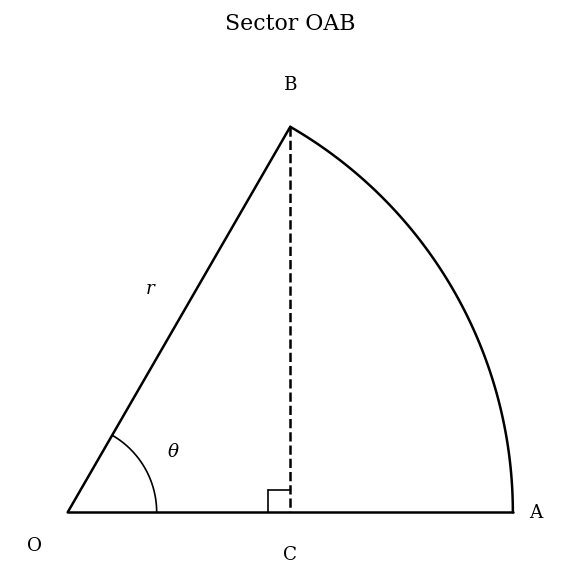
Derive an expression for the area of triangle in terms of and .
Find an expression for the length of the segment .
Calculate the length of the arc AB in terms of and .
A flying drone is programmed to complete a series of movements in a horizontal plane relative to an origin and a set of --axes. In each case, the drone moves to a new position represented by the following transformations:
Write down the matrix for each of the three transformations:
(i) rotation anticlockwise of radians about
(ii) reflection in the line
(iii) rotation clockwise of radians about
Find a single matrix that defines a transformation that represents the overall change in position by multiplying the three matrices in the correct order.
Find .
Hence state what the value of indicates for the possible movement of the drone.
Three drones are initially positioned at the points , and . After performing the movements listed above, the drones are positioned at points , and respectively.
Show that the area of triangle is equal to the area of triangle .
Find a single transformation that is equivalent to the three transformations represented by matrix .
Solve the equation for .
A sector of a circle has a radius of 10 cm and subtends an angle of radians at the centre of the circle.
Calculate the arc length of the sector.
Find the area of the sector.
Draw a diagram of the circle, shading the given sector that subtends an angle of .
Consider the function $f(x) = 2\sin^2 x + 7\sin 2x + \tan x - 9$, where $0 \leqslant x < \frac{\pi}{2}$.
Let $u = \tan x$.
Express $\sin x$ in terms of $u$.
Express $\sin 2x$ in terms of $u$.
Hence show that $f(x) = 0$ can be expressed as $u^3 - 7u^2 + 15u - 9 = 0$.
Determine an expression for $f'(x)$ in terms of $x$.
Solve the equation $f(x) = 0$, giving your answers in the form $\arctan k$ where $k \in \mathbb{Z}$.
A ball is attached to the end of a string and spun horizontally. Its position relative to a given point, $\text{O}$, at time $t$ seconds, $t \geq 0$, is given by the equation
$\mathbf{r} = \begin{pmatrix} 1.5 \cos(0.1t^2) \\ 1.5 \sin(0.1t^2) \end{pmatrix}$
where all displacements are in metres.
The string breaks when the magnitude of the ball’s acceleration exceeds $20 \text{ ms}^{-2}$.
Show that the ball is moving in a circle with its centre at $\text{O}$ and state the radius of the circle.
Find an expression for the velocity of the ball at time $t$.
Hence show that the velocity of the ball is always perpendicular to the position vector of the ball.
Find an expression for the acceleration of the ball at time $t$.
Find the value of $t$ at the instant the string breaks.
How many complete revolutions has the ball completed from $t=0$ to the instant at which the string breaks?
Consider an equilateral triangle where each side has a length of metre. Let be the midpoint of the segment , and let be the third vertex such that is the altitude of the triangle. The point is the midpoint of the segment . A circular arc, centered at , passes through the points and , forming a shaded region (a circular segment) bounded by the arc and the chord .
Calculate the radius, , of the circular arc.
Find the area of the shaded region.
Find the length of the circular arc .
Calculate the area of the equilateral triangle .
Find the area of the shaded region as a fraction of the area of triangle .
Practice AHL 3.7—Radians with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
Convert radians to degrees.
Determine the value of .
Explain why angles measured in radians are dimensionless quantities.
A circle has a radius of 5 cm.
Express an angle of in radians.
Find the area of the sector subtended by the angle .
Determine the length of the arc subtended by the angle .
The lengths of two of the sides in a triangle are cm and cm. Let be the angle between the two given sides. The triangle has an area of cm.
Show that .
Find the two possible values for the length of the third side.
The figure shows sector OAB of a circle with centre O and radius cm. The angle subtended at the centre, , lies between . A perpendicular line is drawn from the point to meet the radius at the point , forming the right triangle .

Derive an expression for the area of triangle in terms of and .
Find an expression for the length of the segment .
Calculate the length of the arc AB in terms of and .
A flying drone is programmed to complete a series of movements in a horizontal plane relative to an origin and a set of --axes. In each case, the drone moves to a new position represented by the following transformations:
Write down the matrix for each of the three transformations:
(i) rotation anticlockwise of radians about
(ii) reflection in the line
(iii) rotation clockwise of radians about
Find a single matrix that defines a transformation that represents the overall change in position by multiplying the three matrices in the correct order.
Find .
Hence state what the value of indicates for the possible movement of the drone.
Three drones are initially positioned at the points , and . After performing the movements listed above, the drones are positioned at points , and respectively.
Show that the area of triangle is equal to the area of triangle .
Find a single transformation that is equivalent to the three transformations represented by matrix .
Solve the equation for .
A sector of a circle has a radius of 10 cm and subtends an angle of radians at the centre of the circle.
Calculate the arc length of the sector.
Find the area of the sector.
Draw a diagram of the circle, shading the given sector that subtends an angle of .
Consider the function $f(x) = 2\sin^2 x + 7\sin 2x + \tan x - 9$, where $0 \leqslant x < \frac{\pi}{2}$.
Let $u = \tan x$.
Express $\sin x$ in terms of $u$.
Express $\sin 2x$ in terms of $u$.
Hence show that $f(x) = 0$ can be expressed as $u^3 - 7u^2 + 15u - 9 = 0$.
Determine an expression for $f'(x)$ in terms of $x$.
Solve the equation $f(x) = 0$, giving your answers in the form $\arctan k$ where $k \in \mathbb{Z}$.
A ball is attached to the end of a string and spun horizontally. Its position relative to a given point, $\text{O}$, at time $t$ seconds, $t \geq 0$, is given by the equation
$\mathbf{r} = \begin{pmatrix} 1.5 \cos(0.1t^2) \\ 1.5 \sin(0.1t^2) \end{pmatrix}$
where all displacements are in metres.
The string breaks when the magnitude of the ball’s acceleration exceeds $20 \text{ ms}^{-2}$.
Show that the ball is moving in a circle with its centre at $\text{O}$ and state the radius of the circle.
Find an expression for the velocity of the ball at time $t$.
Hence show that the velocity of the ball is always perpendicular to the position vector of the ball.
Find an expression for the acceleration of the ball at time $t$.
Find the value of $t$ at the instant the string breaks.
How many complete revolutions has the ball completed from $t=0$ to the instant at which the string breaks?
Consider an equilateral triangle where each side has a length of metre. Let be the midpoint of the segment , and let be the third vertex such that is the altitude of the triangle. The point is the midpoint of the segment . A circular arc, centered at , passes through the points and , forming a shaded region (a circular segment) bounded by the arc and the chord .
Calculate the radius, , of the circular arc.
Find the area of the shaded region.
Find the length of the circular arc .
Calculate the area of the equilateral triangle .
Find the area of the shaded region as a fraction of the area of triangle .