The Voronoi diagram below shows four supermarkets represented by points with coordinates $\mathrm{A}(0,0), \mathrm{B}(6,0), \mathrm{C}(0,6)$ and $\mathrm{D}(2,2)$. The vertices $\mathrm{X}, \mathrm{Y}, \mathrm{Z}$ are also shown. All distances are measured in kilometres. 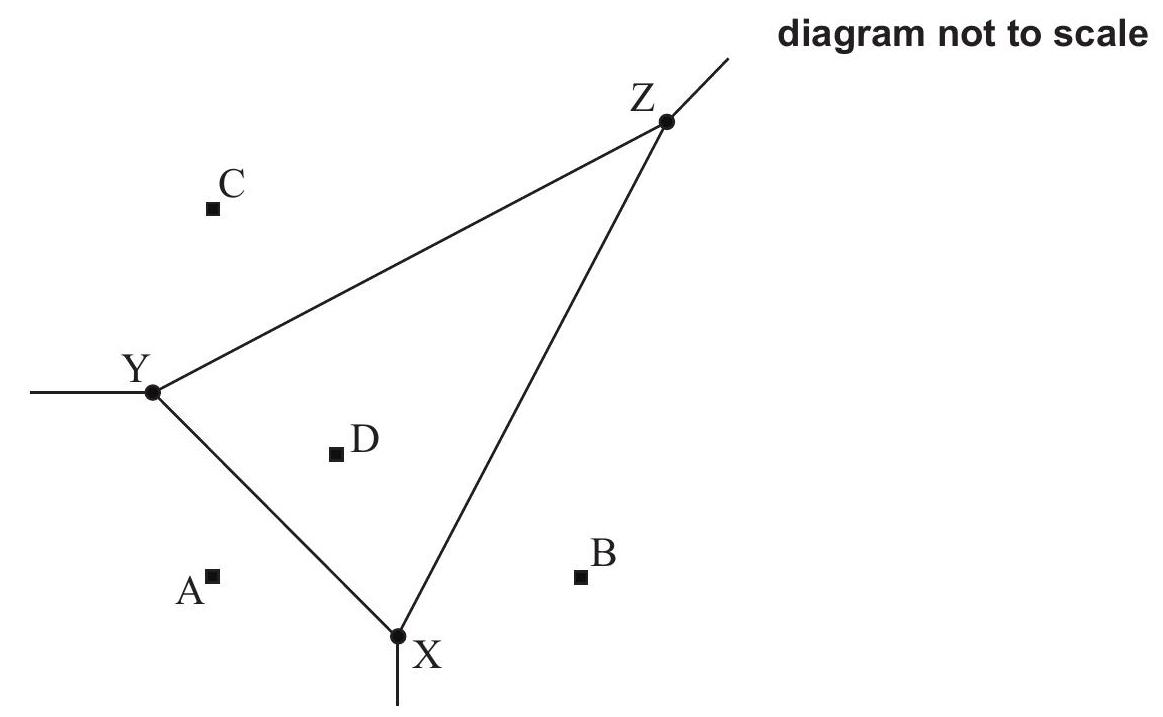The equation of (XY) is $y=2-x$ and the equation of $(\mathrm{YZ})$ is $y=0.5 x+3.5$. The coordinates of Y are $(-1,3)$ and the coordinates of Z are $(7,7)$.

attempt to use distance formula $YZ=\sqrt{(7-(-1))^{2}+(7-3)^{2}}$ $=\sqrt{80}(4\sqrt{5})$

METHOD 1 (cosine rule) length of XZ is $\sqrt{80}(4\sqrt{5}, 8.94427\ldots)$ Note: Accept 8.94 and 8.9 attempt to substitute into cosine rule $\cos X\hat{Y}Z=\frac{80+32-80}{2\times\sqrt{80}\sqrt{32}}$ $(=0.316227\ldots)$ Note: Award $\boldsymbol{A1}$ for correct substitution of XZ, YZ, $\sqrt{32}$ values in the cos rule. Exact values do not need to be used in the substitution. $(X\hat{Y}Z=) 71.6^{\circ}(71.5650\ldots^{\circ})$ Note: Last $\boldsymbol{A1}$ mark may be lost if prematurely rounded values of XZ , YZ and/or XY are used.

METHOD 2 (splitting isosceles triangle in half) length of XZ is $\sqrt{80}(4\sqrt{5}, 8.94427\ldots)$ Note: Accept 8.94 and 8.9. required angle is $\cos^{-1}\left(\frac{\sqrt{32}}{2\sqrt{80}}\right)$ Note: Award A1 for correct substitution of XZ (or YZ), $\frac{\sqrt{32}}{2}$ values in the cos rule. Exact values do not need to be used in the substitution. $(X\hat{Y}Z=) 71.6^{\circ}(71.5650^{\circ})$ Note: Last $\boldsymbol{A1}$ mark may be lost if prematurely rounded values of XZ , YZ and/or XY are used.

$(\text{area}=)\frac{1}{2}\sqrt{80}\sqrt{32}\sin 71.5650\ldots$ OR $(\text{area}=)\frac{1}{2}\sqrt{32}\sqrt{72}$ $=24 \text{ km}^2$

Any sensible answer such as:

There might be factors other than proximity which influence shopping choices. A larger area does not necessarily result in an increase in population. The supermarkets might be specialized / have a particular clientele who visit even if other shops are closer. Transport links might not be represented by Euclidean distances. etc.