Practice SL 5.7—Optimisation with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
A sustainable fashion company produces and sells eco-friendly clothing. The profit, in dollars, from selling units of a particular clothing item is given by:
Determine the number of units that maximises the profit.
Calculate the maximum profit.
Determine whether the function has a point of inflection, showing all necessary steps.
A point lies on the parabola . Points and lie on the x-axis. Let be the sum of distances and .
Express in terms of .
Let . Find the derivative .
Find the value of that minimizes , and justify that it is a minimum.
Calculate the minimum sum of distances and the coordinates of .
Sketch the parabola and points , indicating the minimum distance paths.
A composite shape consists of a hemisphere of radius attached to the top of a cylinder of radius and height . The total volume is , and the cost of material is \ 0.05\mathrm{cm}^{2}$ 0.03\mathrm{cm}^{2}$ for the flat base.
Show that .
Derive an expression for the total cost in dollars in terms of .
Find the value of that minimizes the cost, and calculate the minimum cost. Justify your answer.
Calculate the height and the total surface area at the minimum cost.
An open-top tank with a square base is designed to have a total surface area of . Let the side length of the square base be metres, and the height of the tank be metres, as shown in the figure below.
Show that the height of the tank can be expressed as:
Write an expression for the volume of the tank in terms of only.
Use differentiation to find the value of that maximises the volume of the tank.
Calculate the height of the tank when the volume is maximised, and hence determine the maximum volume.
A factory packages coconut water in cone-shaped containers with a base radius of 5.2 cm and a height of 13 cm.
The factory designers are currently investigating whether a cone-shaped container can be replaced with a cylinder-shaped container with the same radius and the same total surface area.
Find the slant height of the cone-shaped container.
Show that the total surface area of the cone-shaped container is 314 cm2, correct to three significant figures.
Find the height, $h$, of this cylinder-shaped container.
The factory director wants to increase the volume of coconut water sold per container.
State whether or not they should replace the cone-shaped containers with cylinder‑shaped containers. Justify your conclusion.
A company produces units of a product weekly, with revenue modeled by dollars and cost by dollars. Additionally, the company must store unsold units, with storage cost dollars.
Write an expression for the total profit .
Find the derivative .
Determine the production level that maximizes profit, and calculate the maximum profit. Justify your answer.
If the company can only produce between 100 and 300 units, find the production level that minimizes storage cost and compare its profit to the global maximum found in Part 3.
A company's profit per year was found to be changing at a rate of where is the company's profit in thousands of dollars and is the time since the company was founded, measured in years.
Determine whether the profit is increasing or decreasing when .
One year after the company was founded, the profit was thousand dollars. Find an expression for , when .
A cylindrical water tank has a radius and height , with a total surface area (including top and bottom) of .
Express in terms of .
Show that the volume of the tank is given by .
Find the radius that maximizes the volume, and calculate the maximum volume. Justify your answer.
The depth of water in a port is modelled by the function $d(t) = p\cos qt + 7.5$, for $0 \leqslant t \leqslant 12$, where $t$ is the number of hours after high tide.
At high tide, the depth is 9.7 metres.
At low tide, which is 7 hours later, the depth is 5.3 metres.
Find the value of $p$.
Find the value of $q$.
Use the model to find the depth of the water 10 hours after high tide.
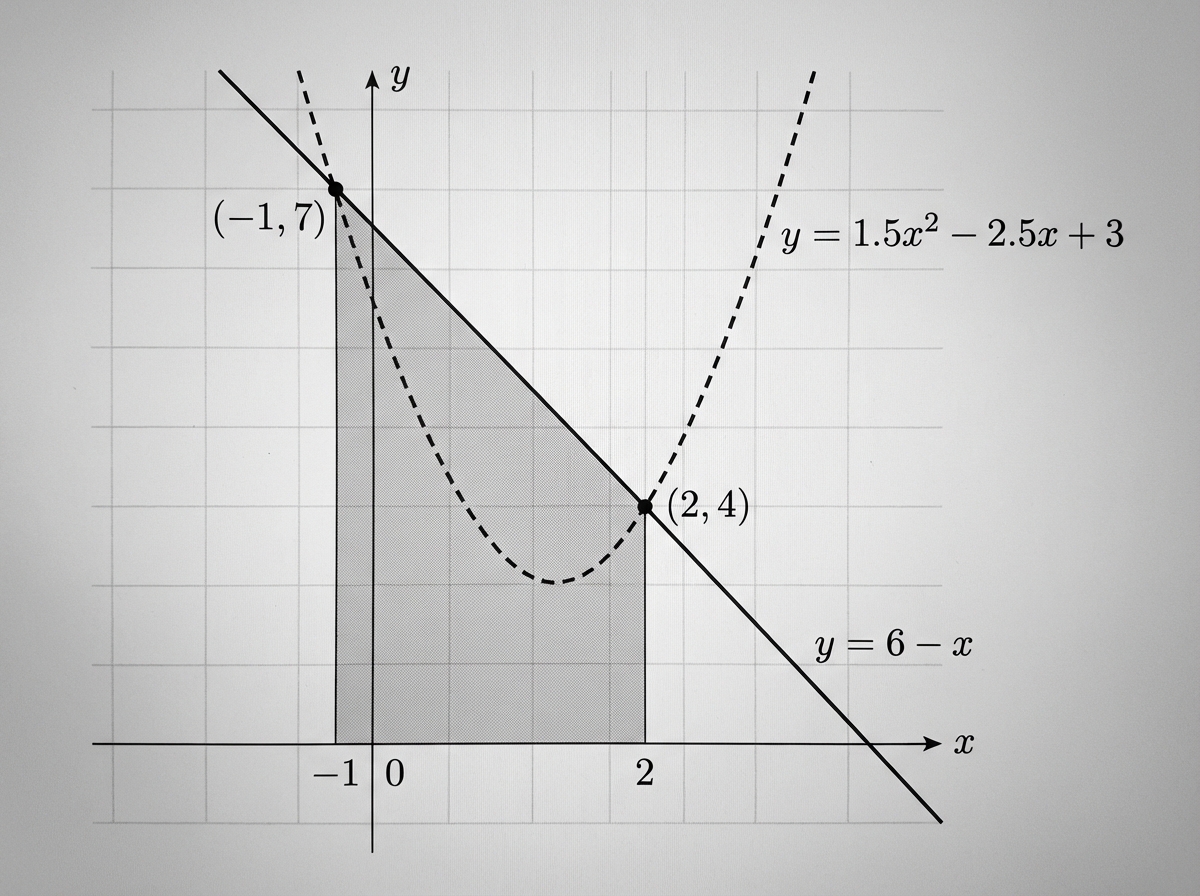
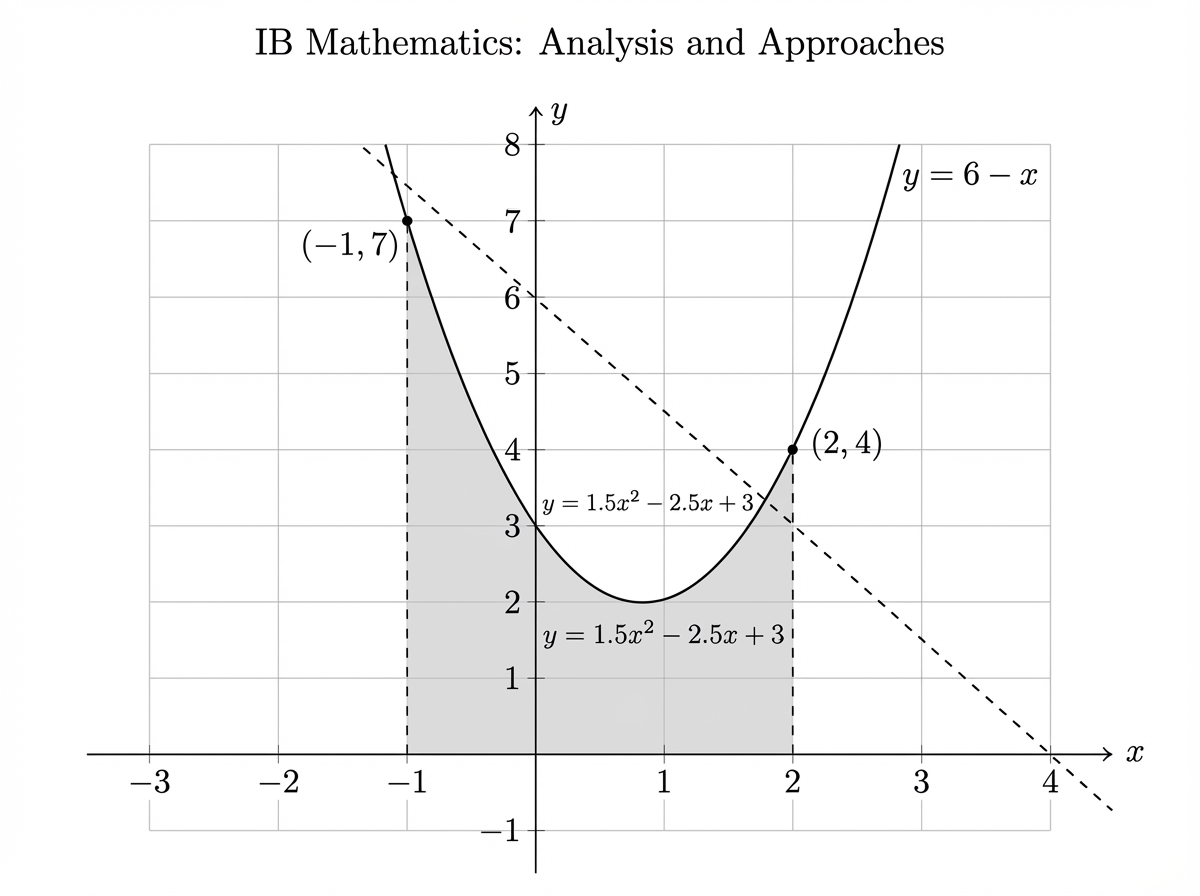
The graphs of and intersect at and , as shown in the following diagrams.
In Diagram 1, the region enclosed by the line , the vertical lines and , and the -axis has been shaded.
In Diagram 2, the region enclosed by the curve , the vertical lines and , and the -axis has been shaded.
Calculate the area of the shaded region in Diagram 1.
Write down an integral for the area of the shaded region in Diagram 2.
Calculate the area of the shaded region in Diagram 2.
Hence, determine the area enclosed between the line and the curve .
Practice SL 5.7—Optimisation with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
A sustainable fashion company produces and sells eco-friendly clothing. The profit, in dollars, from selling units of a particular clothing item is given by:
Determine the number of units that maximises the profit.
Calculate the maximum profit.
Determine whether the function has a point of inflection, showing all necessary steps.
A point lies on the parabola . Points and lie on the x-axis. Let be the sum of distances and .
Express in terms of .
Let . Find the derivative .
Find the value of that minimizes , and justify that it is a minimum.
Calculate the minimum sum of distances and the coordinates of .
Sketch the parabola and points , indicating the minimum distance paths.
A composite shape consists of a hemisphere of radius attached to the top of a cylinder of radius and height . The total volume is , and the cost of material is \ 0.05\mathrm{cm}^{2}$ 0.03\mathrm{cm}^{2}$ for the flat base.
Show that .
Derive an expression for the total cost in dollars in terms of .
Find the value of that minimizes the cost, and calculate the minimum cost. Justify your answer.
Calculate the height and the total surface area at the minimum cost.
An open-top tank with a square base is designed to have a total surface area of . Let the side length of the square base be metres, and the height of the tank be metres, as shown in the figure below.
Show that the height of the tank can be expressed as:
Write an expression for the volume of the tank in terms of only.
Use differentiation to find the value of that maximises the volume of the tank.
Calculate the height of the tank when the volume is maximised, and hence determine the maximum volume.
A factory packages coconut water in cone-shaped containers with a base radius of 5.2 cm and a height of 13 cm.
The factory designers are currently investigating whether a cone-shaped container can be replaced with a cylinder-shaped container with the same radius and the same total surface area.
Find the slant height of the cone-shaped container.
Show that the total surface area of the cone-shaped container is 314 cm2, correct to three significant figures.
Find the height, $h$, of this cylinder-shaped container.
The factory director wants to increase the volume of coconut water sold per container.
State whether or not they should replace the cone-shaped containers with cylinder‑shaped containers. Justify your conclusion.
A company produces units of a product weekly, with revenue modeled by dollars and cost by dollars. Additionally, the company must store unsold units, with storage cost dollars.
Write an expression for the total profit .
Find the derivative .
Determine the production level that maximizes profit, and calculate the maximum profit. Justify your answer.
If the company can only produce between 100 and 300 units, find the production level that minimizes storage cost and compare its profit to the global maximum found in Part 3.
A company's profit per year was found to be changing at a rate of where is the company's profit in thousands of dollars and is the time since the company was founded, measured in years.
Determine whether the profit is increasing or decreasing when .
One year after the company was founded, the profit was thousand dollars. Find an expression for , when .
A cylindrical water tank has a radius and height , with a total surface area (including top and bottom) of .
Express in terms of .
Show that the volume of the tank is given by .
Find the radius that maximizes the volume, and calculate the maximum volume. Justify your answer.
The depth of water in a port is modelled by the function $d(t) = p\cos qt + 7.5$, for $0 \leqslant t \leqslant 12$, where $t$ is the number of hours after high tide.
At high tide, the depth is 9.7 metres.
At low tide, which is 7 hours later, the depth is 5.3 metres.
Find the value of $p$.
Find the value of $q$.
Use the model to find the depth of the water 10 hours after high tide.
The graphs of and intersect at and , as shown in the following diagrams.
In Diagram 1, the region enclosed by the line , the vertical lines and , and the -axis has been shaded.

In Diagram 2, the region enclosed by the curve , the vertical lines and , and the -axis has been shaded.

Calculate the area of the shaded region in Diagram 1.
Write down an integral for the area of the shaded region in Diagram 2.
Calculate the area of the shaded region in Diagram 2.
Hence, determine the area enclosed between the line and the curve .