Practice AHL 5.17—Phase portrait with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
A researcher is analyzing the growth of two interacting plant species in a controlled environment. The growth rates of species X and species Y can be described by the following system of differential equations:
Find the eigenvalues of the coefficient matrix.
A biologist is studying the interaction between two species in an ecosystem, where the population dynamics can be modeled by the following system of differential equations:
Determine the eigenvalues of the system.
Find the corresponding eigenvectors.
Classify the origin and describe the behaviour of solutions near it.
Suggest a practical interpretation of this system in terms of population dynamics.
This question will investigate the solution to a coupled system of differential equations when there is only one eigenvalue.
It is desired to solve the coupled system of differential equations
The general solution to the coupled system of differential equations is hence given by
Show that the matrix
has only one eigenvalue. Find this eigenvalue and an associated eigenvector.
Hence, verify that
is a solution to the above system.
Verify that
is also a solution.
If initially at , , , find the particular solution.
Find the values of and when .
Determine the limiting value of the ratio as and hence state the equation of the line passing through the origin to which the trajectory becomes parallel.
State the quadrant in which the trajectory lies as and describe its motion relative to the origin.
The diagram shows the slope field for the differential equation . The graphs of the two solutions to the differential equation that pass through points and are shown.
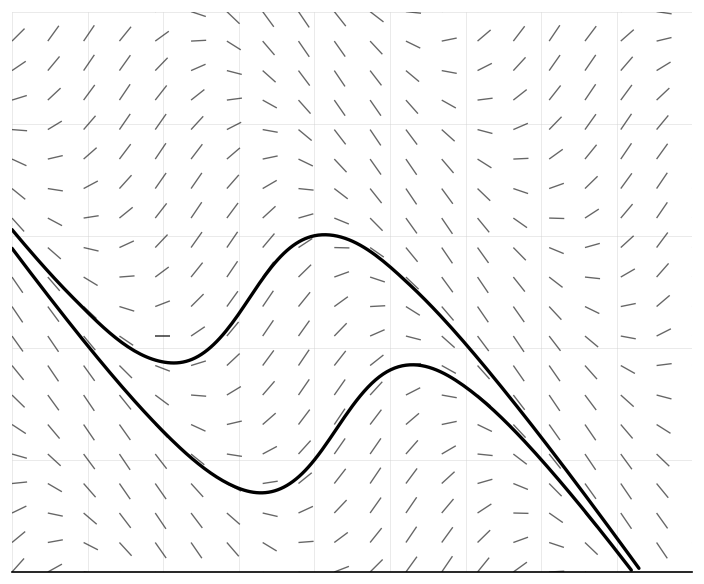
For the two solutions given, the local minimum points lie on the straight line .
Find the equation of , giving your answer in the form .
For the two solutions given, the local maximum points lie on the straight line . Find the equation of .
A biologist is studying the population dynamics of two species in a shared habitat. The change in population of species X and species Y over time can be modeled by the following system of differential equations:
Determine the characteristic equation of the system and hence find the eigenvalues.
Determine if the origin is stable or unstable based on the eigenvalues.
Describe the shape of the trajectories near the origin based on the eigenvalues.
A model describes the dynamics of two chemical concentrations, and (in mol/L), in a reactor, governed by the system:
This system has a single eigenvalue.
Show that the matrix has only one eigenvalue, and find it along with an associated eigenvector.
Verify that is a solution to the system.
Find a second independent solution of the form , and verify it.
Given initial conditions , find the particular solution.
Sketch the phase portrait for , showing the equilibrium point, an eigenvector direction, and at least two trajectories with arrows.
This question will investigate the solution to a coupled system of differential equations and how to transform it to a system that can be solved by the eigenvector method. It is desired to solve the coupled system of differential equations where and represent the population of two types of symbiotic coral and is time measured in decades.
Find the equilibrium point for this system.
If initially and , use Euler's method with a time increment of 0.1 to find an approximation for the values of and when .
Extend this method to conjecture the limit of the ratio as .
Show how using the substitution transforms the system of differential equations into
Solve this system of equations by the eigenvalue method and hence find the general solution for of the original system.
Find the particular solution to the original system, given the initial conditions of part 2.
Hence find the exact values of and when , giving the answers to 4 significant figures.
Use part 6 to find limit of the ratio as .
With the initial conditions as given in part 2, determine if the populations converge to the equilibrium values.
If instead the initial conditions were given as and , find the particular solution for of the original system, in this case.
With the initial conditions as given in part 10, determine if the populations converge to the equilibrium values.
The populations of two symbiotic bacteria, and , in a petri dish are modeled by:
where and are in millions per and is in hours.
Find the general solution using the eigenvalue method.
Given initial conditions , find the particular solution.
Determine the asymptotic behavior of the particular solution as , including the equation of the asymptote.
Sketch the phase portrait for , showing the asymptote and at least two trajectories with arrows.
A model for the populations of two symbiotic algae species, and (in thousands per ), is given by:
Find the equilibrium point.
Use the substitution to transform the system into a homogeneous system, and find its eigenvalues.
Find the general solution of the original system, using the eigenvalues and eigenvectors determined in part 2.
Given initial conditions , find the particular solution and determine the limit of as .
Sketch the phase portrait for , showing the equilibrium point and trajectories.
An environmental scientist is asked by a river authority to model the effect of a leak from a power plant on the mercury levels in a local river. The variable measures the concentration of mercury in micrograms per litre () at time days.
The initial mercury concentration is and the rate of increase is initially .
Show that the system of coupled first order equations: can be written as the second order differential equation:
Find the eigenvalues of the system of coupled first order equations given in part 1.
Hence find the exact solution of the second order differential equation.
Sketch the graph of against , labelling the maximum point of the graph with its coordinates.
The river authority decides that fishing should be stopped when the mercury concentration exceeds .
Use the model to calculate the total amount of time when fishing should be stopped.
Write down one reason, with reference to the context, to support this decision.
Practice AHL 5.17—Phase portrait with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
A researcher is analyzing the growth of two interacting plant species in a controlled environment. The growth rates of species X and species Y can be described by the following system of differential equations:
Find the eigenvalues of the coefficient matrix.
A biologist is studying the interaction between two species in an ecosystem, where the population dynamics can be modeled by the following system of differential equations:
Determine the eigenvalues of the system.
Find the corresponding eigenvectors.
Classify the origin and describe the behaviour of solutions near it.
Suggest a practical interpretation of this system in terms of population dynamics.
This question will investigate the solution to a coupled system of differential equations when there is only one eigenvalue.
It is desired to solve the coupled system of differential equations
The general solution to the coupled system of differential equations is hence given by
Show that the matrix
has only one eigenvalue. Find this eigenvalue and an associated eigenvector.
Hence, verify that
is a solution to the above system.
Verify that
is also a solution.
If initially at , , , find the particular solution.
Find the values of and when .
Determine the limiting value of the ratio as and hence state the equation of the line passing through the origin to which the trajectory becomes parallel.
State the quadrant in which the trajectory lies as and describe its motion relative to the origin.
The diagram shows the slope field for the differential equation . The graphs of the two solutions to the differential equation that pass through points and are shown.

For the two solutions given, the local minimum points lie on the straight line .
Find the equation of , giving your answer in the form .
For the two solutions given, the local maximum points lie on the straight line . Find the equation of .
A biologist is studying the population dynamics of two species in a shared habitat. The change in population of species X and species Y over time can be modeled by the following system of differential equations:
Determine the characteristic equation of the system and hence find the eigenvalues.
Determine if the origin is stable or unstable based on the eigenvalues.
Describe the shape of the trajectories near the origin based on the eigenvalues.
A model describes the dynamics of two chemical concentrations, and (in mol/L), in a reactor, governed by the system:
This system has a single eigenvalue.
Show that the matrix has only one eigenvalue, and find it along with an associated eigenvector.
Verify that is a solution to the system.
Find a second independent solution of the form , and verify it.
Given initial conditions , find the particular solution.
Sketch the phase portrait for , showing the equilibrium point, an eigenvector direction, and at least two trajectories with arrows.
This question will investigate the solution to a coupled system of differential equations and how to transform it to a system that can be solved by the eigenvector method. It is desired to solve the coupled system of differential equations where and represent the population of two types of symbiotic coral and is time measured in decades.
Find the equilibrium point for this system.
If initially and , use Euler's method with a time increment of 0.1 to find an approximation for the values of and when .
Extend this method to conjecture the limit of the ratio as .
Show how using the substitution transforms the system of differential equations into
Solve this system of equations by the eigenvalue method and hence find the general solution for of the original system.
Find the particular solution to the original system, given the initial conditions of part 2.
Hence find the exact values of and when , giving the answers to 4 significant figures.
Use part 6 to find limit of the ratio as .
With the initial conditions as given in part 2, determine if the populations converge to the equilibrium values.
If instead the initial conditions were given as and , find the particular solution for of the original system, in this case.
With the initial conditions as given in part 10, determine if the populations converge to the equilibrium values.
The populations of two symbiotic bacteria, and , in a petri dish are modeled by:
where and are in millions per and is in hours.
Find the general solution using the eigenvalue method.
Given initial conditions , find the particular solution.
Determine the asymptotic behavior of the particular solution as , including the equation of the asymptote.
Sketch the phase portrait for , showing the asymptote and at least two trajectories with arrows.
A model for the populations of two symbiotic algae species, and (in thousands per ), is given by:
Find the equilibrium point.
Use the substitution to transform the system into a homogeneous system, and find its eigenvalues.
Find the general solution of the original system, using the eigenvalues and eigenvectors determined in part 2.
Given initial conditions , find the particular solution and determine the limit of as .
Sketch the phase portrait for , showing the equilibrium point and trajectories.
An environmental scientist is asked by a river authority to model the effect of a leak from a power plant on the mercury levels in a local river. The variable measures the concentration of mercury in micrograms per litre () at time days.
The initial mercury concentration is and the rate of increase is initially .
Show that the system of coupled first order equations: can be written as the second order differential equation:
Find the eigenvalues of the system of coupled first order equations given in part 1.
Hence find the exact solution of the second order differential equation.
Sketch the graph of against , labelling the maximum point of the graph with its coordinates.
The river authority decides that fishing should be stopped when the mercury concentration exceeds .
Use the model to calculate the total amount of time when fishing should be stopped.
Write down one reason, with reference to the context, to support this decision.