- IB
- AHL 5.14—Setting up a DE, solve by separating variables
Practice AHL 5.14—Setting up a DE, solve by separating variables with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
A predator-prey system models the populations of rabbits (, in thousands) and foxes (, in hundreds) in a forest, given by:
where is in years. Initially, .
Find the non-zero equilibrium point for the system.
Interpret the equilibrium point in the context of the model.
Use Euler's method with a step size of 0.2 years to estimate and after 1 year.
Sketch the phase portrait trajectory for , starting from the initial point over the first 2 years.
A disease spreads in a population according to the differential equation
where is the number of infected individuals (in thousands), and is time in days. Initially, . The health authority aims to keep the infected population below 20,000.
Solve the differential equation to find in terms of .
Determine the time when .
Use Euler's method with a step size of 0.1 days to estimate after 0.2 days.
Sketch the phase portrait of against for .
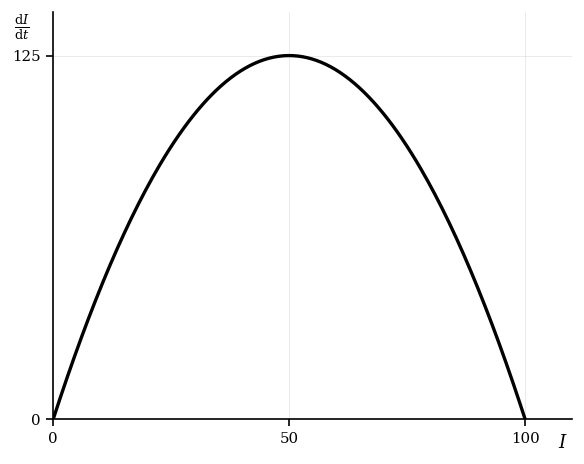
Using the phase portrait, or otherwise, determine if the infected population will exceed 20,000 in the first 10 days.
An object is placed into the top of a long vertical tube filled with a thick viscous fluid at time seconds.
Initially, it is thought that the resistance of the fluid would be proportional to the velocity of the object. The following model was proposed, where the object’s displacement, , from the top of the tube, measured in metres, is given by the differential equation
The maximum velocity approached by the object as it falls is known as the terminal velocity.
An experiment is performed in which the object is placed in the fluid on a number of occasions and its terminal velocity recorded. It is found that the terminal velocity was consistently smaller than that predicted by the model used. It was suggested that the resistance to motion is actually proportional to the velocity squared and so the following model was set up:
At terminal velocity, the acceleration of an object is equal to zero.
By substituting into the equation, find an expression for the velocity of the object at time . Give your answer in the form .
From your solution to part 1, or otherwise, find the terminal velocity of the object predicted by this model.
Write down the differential equation for the second model as a system of first-order differential equations.
Use Euler’s method, with a step length of , to find the displacement and velocity of the object when .
By repeated application of Euler’s method, find an approximation for the terminal velocity, to five significant figures.
Use the differential equation to find the exact terminal velocity for the object predicted by the second model.
Use your answers to parts 4, 5 and 6 to comment on the accuracy of the Euler approximation to this model.
A local community is facing environmental challenges due to a chemical leak into a nearby lake. The concentration of the pollutant in the lake, denoted as , decreases over time at a rate proportional to its current concentration. Understanding this decay is crucial for the community to manage the lake's health and plan for remediation efforts.
Derive the differential equation that models the concentration .
Solve the differential equation for .
Given that the initial concentration is and that the concentration drops to in hours, find the value of the constant of proportionality .
How long will it take for the concentration to drop to ?
A café is known for its freshly brewed tea, which cools down over time. According to Newton's Law of Cooling, the rate at which the temperature of the tea decreases is proportional to the difference between the temperature of the tea and the ambient room temperature, which is maintained at .
Write down the differential equation for the temperature of the tea.
Find an expression for the temperature in terms of time .
If the initial temperature of the tea is , find the temperature after 10 minutes, given that .
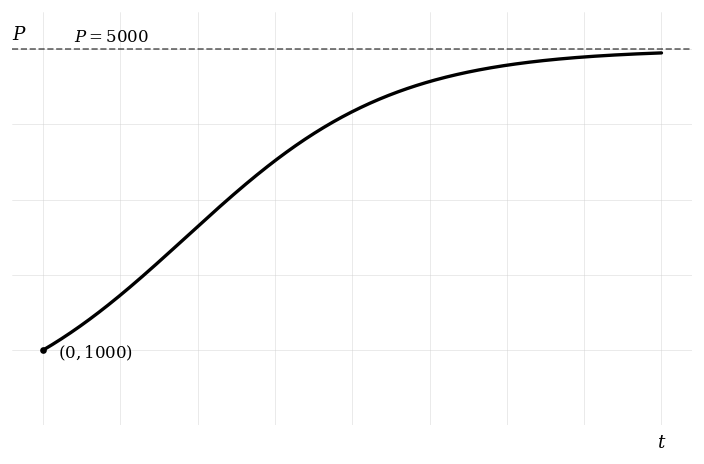
A population of bacteria in a petri dish grows according to the differential equation
where is the number of bacteria and is time in hours. Initially, at , there are 1000 bacteria.
Solve the differential equation to find in terms of .
Find the time taken for the population to reach 4000 bacteria.
Sketch the graph of against for , indicating the carrying capacity and initial condition.
This question will investigate the solution to a coupled system of differential equations when there is only one eigenvalue.
It is desired to solve the coupled system of differential equations
The general solution to the coupled system of differential equations is hence given by
Show that the matrix
has only one eigenvalue. Find this eigenvalue and an associated eigenvector.
Hence, verify that
is a solution to the above system.
Verify that
is also a solution.
If initially at , , , find the particular solution.
Find the values of and when .
Determine the limiting value of the ratio as and hence state the equation of the line passing through the origin to which the trajectory becomes parallel.
State the quadrant in which the trajectory lies as and describe its motion relative to the origin.
A tank of water initially contains $400$ litres. Water is leaking from the tank such that after $10$ minutes there are $324$ litres remaining in the tank.
The volume of water, $V$ litres, remaining in the tank after $t$ minutes, can be modelled by the differential equation
$$ \frac{\mathrm{d}V}{\mathrm{d}t} = -k\sqrt{V} $$
where $k$ is a constant.
Show that $V=\left(20-\frac{t}{5}\right)^2$.
Find the time taken for the tank to empty.
A pollutant in a lake has a concentration (mg per litre) that decreases due to natural dilution. The rate of change is given by
where is in days. Initially, at .
Solve the differential equation to find in terms of .
Find the concentration after 10 days.
Determine the time when the concentration falls below 5 mg per litre.
A chemical reaction produces a substance with concentration that changes according to
where is time in seconds. Initially, at .
Solve the differential equation to find in terms of .
Find the concentration after 2 seconds.
Determine the limiting concentration as .
Practice AHL 5.14—Setting up a DE, solve by separating variables with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
A predator-prey system models the populations of rabbits (, in thousands) and foxes (, in hundreds) in a forest, given by:
where is in years. Initially, .
Find the non-zero equilibrium point for the system.
Interpret the equilibrium point in the context of the model.
Use Euler's method with a step size of 0.2 years to estimate and after 1 year.
Sketch the phase portrait trajectory for , starting from the initial point over the first 2 years.
A disease spreads in a population according to the differential equation
where is the number of infected individuals (in thousands), and is time in days. Initially, . The health authority aims to keep the infected population below 20,000.
Solve the differential equation to find in terms of .
Determine the time when .
Use Euler's method with a step size of 0.1 days to estimate after 0.2 days.
Sketch the phase portrait of against for .

Using the phase portrait, or otherwise, determine if the infected population will exceed 20,000 in the first 10 days.
An object is placed into the top of a long vertical tube filled with a thick viscous fluid at time seconds.
Initially, it is thought that the resistance of the fluid would be proportional to the velocity of the object. The following model was proposed, where the object’s displacement, , from the top of the tube, measured in metres, is given by the differential equation
The maximum velocity approached by the object as it falls is known as the terminal velocity.
An experiment is performed in which the object is placed in the fluid on a number of occasions and its terminal velocity recorded. It is found that the terminal velocity was consistently smaller than that predicted by the model used. It was suggested that the resistance to motion is actually proportional to the velocity squared and so the following model was set up:
At terminal velocity, the acceleration of an object is equal to zero.
By substituting into the equation, find an expression for the velocity of the object at time . Give your answer in the form .
From your solution to part 1, or otherwise, find the terminal velocity of the object predicted by this model.
Write down the differential equation for the second model as a system of first-order differential equations.
Use Euler’s method, with a step length of , to find the displacement and velocity of the object when .
By repeated application of Euler’s method, find an approximation for the terminal velocity, to five significant figures.
Use the differential equation to find the exact terminal velocity for the object predicted by the second model.
Use your answers to parts 4, 5 and 6 to comment on the accuracy of the Euler approximation to this model.
A local community is facing environmental challenges due to a chemical leak into a nearby lake. The concentration of the pollutant in the lake, denoted as , decreases over time at a rate proportional to its current concentration. Understanding this decay is crucial for the community to manage the lake's health and plan for remediation efforts.
Derive the differential equation that models the concentration .
Solve the differential equation for .
Given that the initial concentration is and that the concentration drops to in hours, find the value of the constant of proportionality .
How long will it take for the concentration to drop to ?
A café is known for its freshly brewed tea, which cools down over time. According to Newton's Law of Cooling, the rate at which the temperature of the tea decreases is proportional to the difference between the temperature of the tea and the ambient room temperature, which is maintained at .
Write down the differential equation for the temperature of the tea.
Find an expression for the temperature in terms of time .
If the initial temperature of the tea is , find the temperature after 10 minutes, given that .
A population of bacteria in a petri dish grows according to the differential equation
where is the number of bacteria and is time in hours. Initially, at , there are 1000 bacteria.
Solve the differential equation to find in terms of .
Find the time taken for the population to reach 4000 bacteria.
Sketch the graph of against for , indicating the carrying capacity and initial condition.

This question will investigate the solution to a coupled system of differential equations when there is only one eigenvalue.
It is desired to solve the coupled system of differential equations
The general solution to the coupled system of differential equations is hence given by
Show that the matrix
has only one eigenvalue. Find this eigenvalue and an associated eigenvector.
Hence, verify that
is a solution to the above system.
Verify that
is also a solution.
If initially at , , , find the particular solution.
Find the values of and when .
Determine the limiting value of the ratio as and hence state the equation of the line passing through the origin to which the trajectory becomes parallel.
State the quadrant in which the trajectory lies as and describe its motion relative to the origin.
A tank of water initially contains $400$ litres. Water is leaking from the tank such that after $10$ minutes there are $324$ litres remaining in the tank.
The volume of water, $V$ litres, remaining in the tank after $t$ minutes, can be modelled by the differential equation
$$ \frac{\mathrm{d}V}{\mathrm{d}t} = -k\sqrt{V} $$
where $k$ is a constant.
Show that $V=\left(20-\frac{t}{5}\right)^2$.
Find the time taken for the tank to empty.
A pollutant in a lake has a concentration (mg per litre) that decreases due to natural dilution. The rate of change is given by
where is in days. Initially, at .
Solve the differential equation to find in terms of .
Find the concentration after 10 days.
Determine the time when the concentration falls below 5 mg per litre.
A chemical reaction produces a substance with concentration that changes according to
where is time in seconds. Initially, at .
Solve the differential equation to find in terms of .
Find the concentration after 2 seconds.
Determine the limiting concentration as .