Practice SL 2.4—Features of a graph with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
A team of environmental scientists is studying the growth of a certain plant species, which can be modeled by the function
This function represents the plant's growth rate over time, where is the number of weeks since planting.
Find the two positive real zeros of the function, which represent the weeks when the growth rate is zero.
[2 marks]
Describe the end behavior of as .
[2 marks]
Sketch the graph of the function for , marking the zeros found in Part 1 and describing the behavior of the plant's growth rate around each zero.
[4 marks]
Consider the function . The graph of is shown in the diagram. The vertex of the graph has coordinates . The graph intersects the x-axis at two points, and .
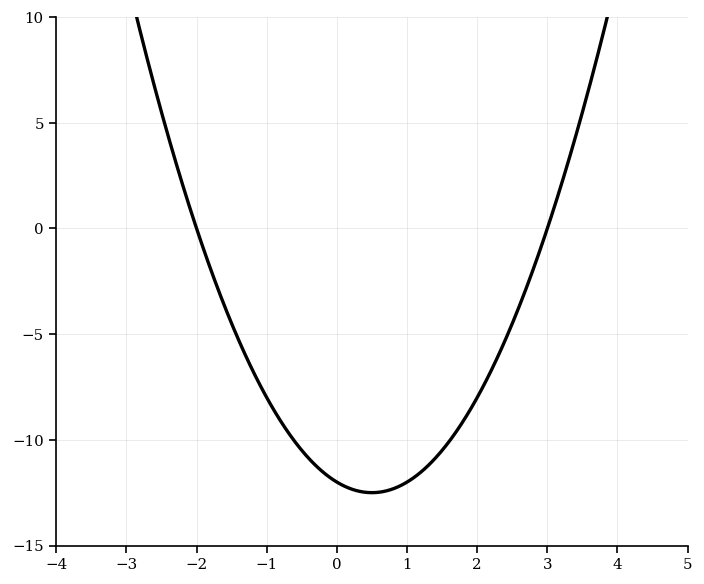
Find the value of .
Find the value of .
Find the value of .
Find the value of .
The depth of water in a port is modelled by the function $d(t) = p\cos qt + 7.5$, for $0 \leqslant t \leqslant 12$, where $t$ is the number of hours after high tide.
At high tide, the depth is 9.7 metres.
At low tide, which is 7 hours later, the depth is 5.3 metres.
Find the value of $p$.
Find the value of $q$.
Use the model to find the depth of the water 10 hours after high tide.
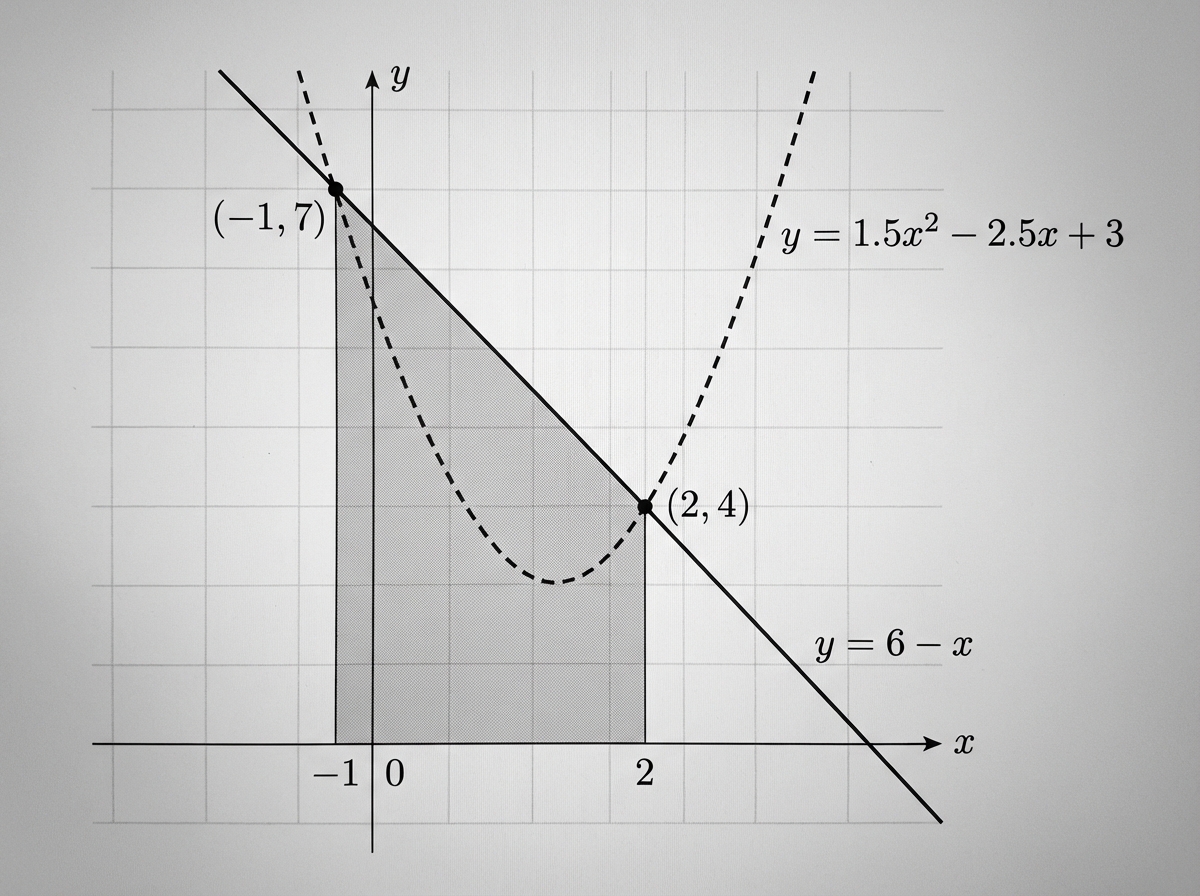
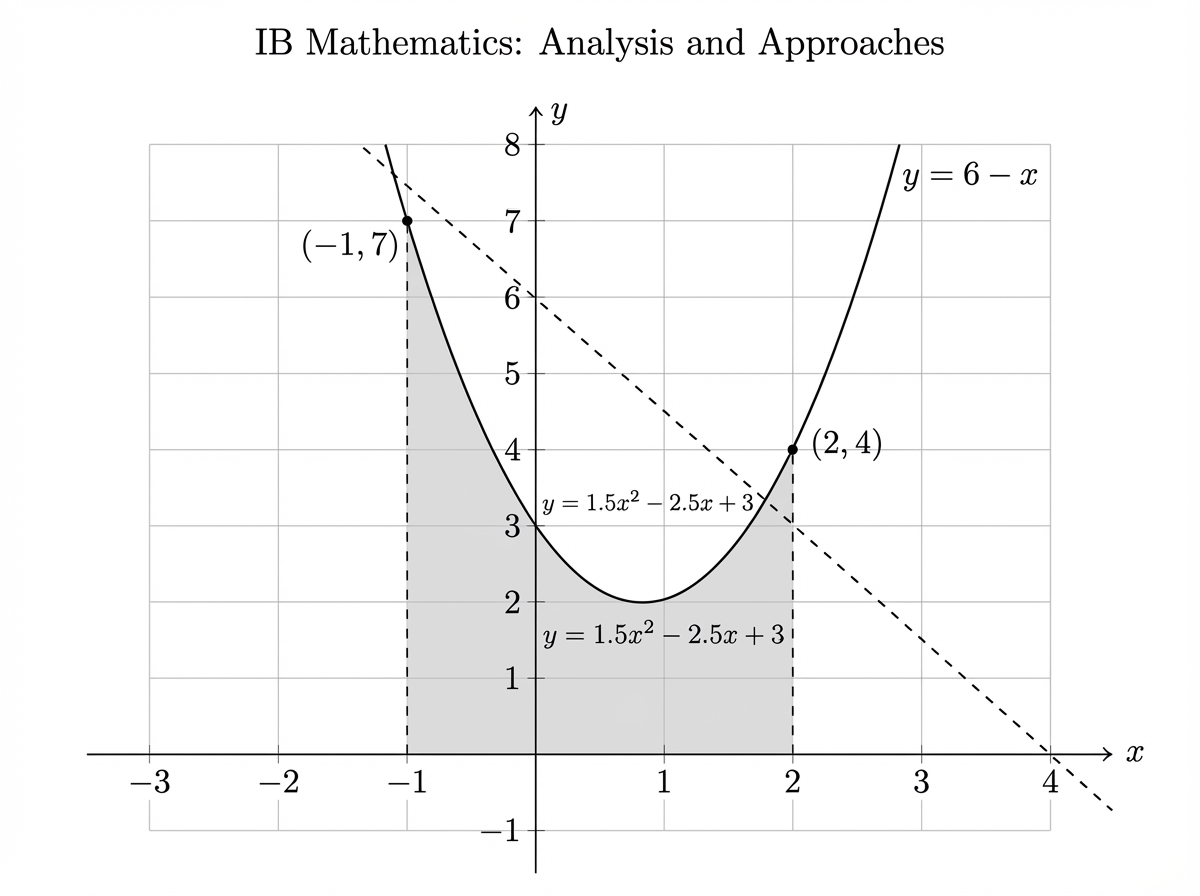
The graphs of and intersect at and , as shown in the following diagrams.
In Diagram 1, the region enclosed by the line , the vertical lines and , and the -axis has been shaded.
In Diagram 2, the region enclosed by the curve , the vertical lines and , and the -axis has been shaded.
Calculate the area of the shaded region in Diagram 1.
Write down an integral for the area of the shaded region in Diagram 2.
Calculate the area of the shaded region in Diagram 2.
Hence, determine the area enclosed between the line and the curve .
A water tank initially contains 5 litres of water. Water is being drained from the tank at a constant rate of 1 litre per minute. The function represents the amount of water (in litres) left in the tank after minutes.
Determine the domain and range of in the context of this problem.
Identify any intercepts on the graph and interpret their meaning in the context of the problem.
Linda owns a field, represented by the shaded region . The plan view of the field is shown in the following diagram, where both axes represent distance and are measured in metres.
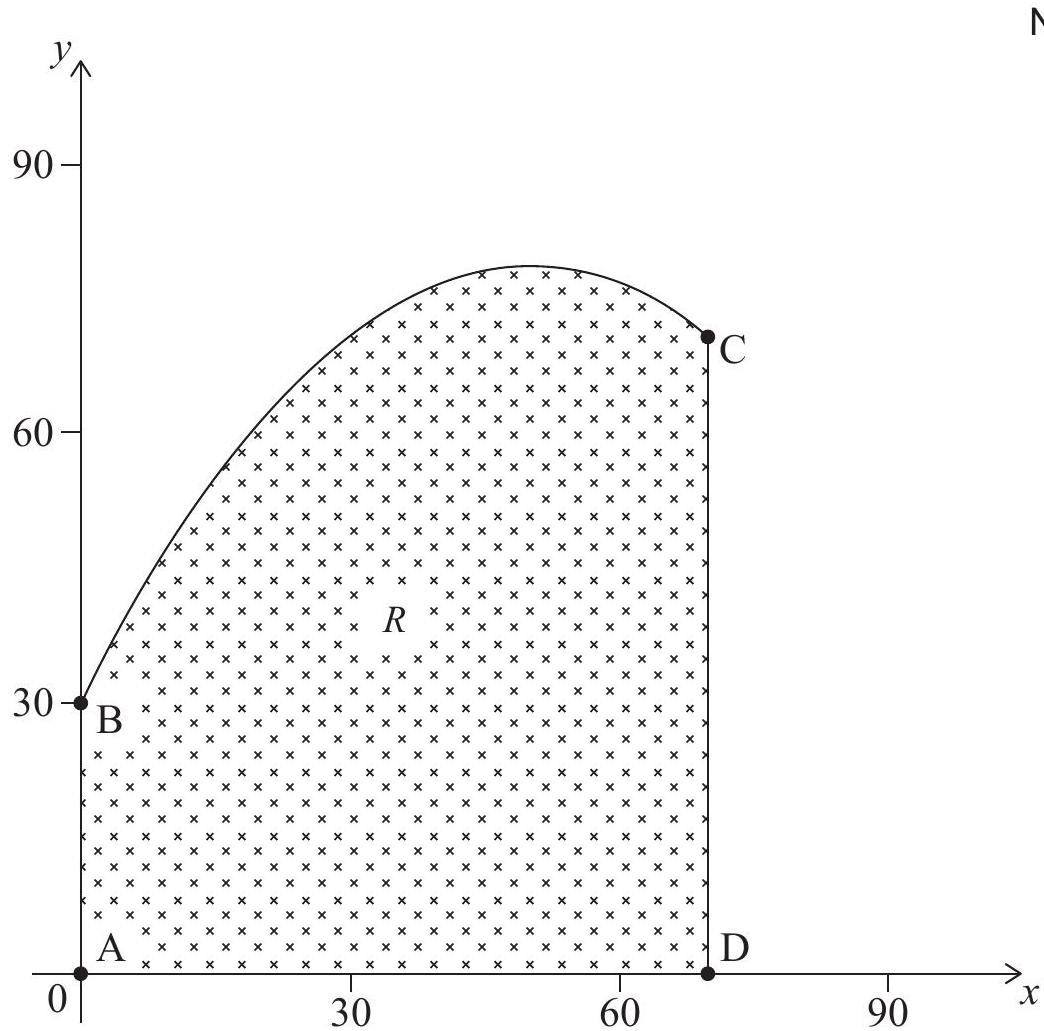
The segments , and respectively represent the western, eastern and southern boundaries of the field. The function models the northern boundary of the field between points and and is given by , for .
Find .
Hence find the coordinates of the point on the field that is furthest north.
Write down the integral which can be used to find the area of the shaded region .
Find the area of Linda's field.
Linda estimates the area of the field to be using the trapezoidal rule. Calculate the percentage error in Linda's estimate.
Suggest how Linda might be able to reduce the error whilst still using the trapezoidal rule.
A building with a square foundation is to be constructed in the field such that lies on , lies on the northern boundary, and and lie on the eastern boundary .
Find the -coordinate of point for the square foundation.
Find the area of the foundation.
A biochemist is analyzing the decay of a radioactive substance, which can be modeled by the function
Here, represents the amount of substance remaining after hours.
Identify the initial value of and the equation of the horizontal asymptote of the function, which indicates the minimum amount of substance that can remain.
A radioactive substance decays exponentially. Initially there are 100 grams of the substance. Determine the decay constant and find the time at which , indicating when half of the substance has decayed.
Sketch the graph of the function , labeling the initial value and the asymptote.
A function is defined by for .
Find the range of .
Find the value of .
The height of a baseball after it is hit by a bat is modelled by the function
$$ h(t) = -4.8t^2 + 21t + 1.2 $$where $h(t)$ is the height in metres above the ground and $t$ is the time in seconds after the ball was hit.
Write down the height of the ball above the ground at the instant it is hit by the bat.
Find the value of $t$ when the ball hits the ground.
State an appropriate domain for $t$ in this model.
A landscape architect is designing a parabolic garden feature, represented by the function
This function describes the height of the garden feature at different horizontal positions .
Identify the vertex of the function and determine the range of heights for the garden feature.
Describe the transformation applied to the basic function to obtain the given function, which reflects the design changes.
Sketch the graph of the garden feature, labeling the vertex and any intercepts.
Practice SL 2.4—Features of a graph with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
A team of environmental scientists is studying the growth of a certain plant species, which can be modeled by the function
This function represents the plant's growth rate over time, where is the number of weeks since planting.
Find the two positive real zeros of the function, which represent the weeks when the growth rate is zero.
[2 marks]
Describe the end behavior of as .
[2 marks]
Sketch the graph of the function for , marking the zeros found in Part 1 and describing the behavior of the plant's growth rate around each zero.
[4 marks]
Consider the function . The graph of is shown in the diagram. The vertex of the graph has coordinates . The graph intersects the x-axis at two points, and .

Find the value of .
Find the value of .
Find the value of .
Find the value of .
The depth of water in a port is modelled by the function $d(t) = p\cos qt + 7.5$, for $0 \leqslant t \leqslant 12$, where $t$ is the number of hours after high tide.
At high tide, the depth is 9.7 metres.
At low tide, which is 7 hours later, the depth is 5.3 metres.
Find the value of $p$.
Find the value of $q$.
Use the model to find the depth of the water 10 hours after high tide.
The graphs of and intersect at and , as shown in the following diagrams.
In Diagram 1, the region enclosed by the line , the vertical lines and , and the -axis has been shaded.

In Diagram 2, the region enclosed by the curve , the vertical lines and , and the -axis has been shaded.

Calculate the area of the shaded region in Diagram 1.
Write down an integral for the area of the shaded region in Diagram 2.
Calculate the area of the shaded region in Diagram 2.
Hence, determine the area enclosed between the line and the curve .
A water tank initially contains 5 litres of water. Water is being drained from the tank at a constant rate of 1 litre per minute. The function represents the amount of water (in litres) left in the tank after minutes.
Determine the domain and range of in the context of this problem.
Identify any intercepts on the graph and interpret their meaning in the context of the problem.
Linda owns a field, represented by the shaded region . The plan view of the field is shown in the following diagram, where both axes represent distance and are measured in metres.

The segments , and respectively represent the western, eastern and southern boundaries of the field. The function models the northern boundary of the field between points and and is given by , for .
Find .
Hence find the coordinates of the point on the field that is furthest north.
Write down the integral which can be used to find the area of the shaded region .
Find the area of Linda's field.
Linda estimates the area of the field to be using the trapezoidal rule. Calculate the percentage error in Linda's estimate.
Suggest how Linda might be able to reduce the error whilst still using the trapezoidal rule.
A building with a square foundation is to be constructed in the field such that lies on , lies on the northern boundary, and and lie on the eastern boundary .
Find the -coordinate of point for the square foundation.
Find the area of the foundation.
A biochemist is analyzing the decay of a radioactive substance, which can be modeled by the function
Here, represents the amount of substance remaining after hours.
Identify the initial value of and the equation of the horizontal asymptote of the function, which indicates the minimum amount of substance that can remain.
A radioactive substance decays exponentially. Initially there are 100 grams of the substance. Determine the decay constant and find the time at which , indicating when half of the substance has decayed.
Sketch the graph of the function , labeling the initial value and the asymptote.
A function is defined by for .
Find the range of .
Find the value of .
The height of a baseball after it is hit by a bat is modelled by the function
$$ h(t) = -4.8t^2 + 21t + 1.2 $$where $h(t)$ is the height in metres above the ground and $t$ is the time in seconds after the ball was hit.
Write down the height of the ball above the ground at the instant it is hit by the bat.
Find the value of $t$ when the ball hits the ground.
State an appropriate domain for $t$ in this model.
A landscape architect is designing a parabolic garden feature, represented by the function
This function describes the height of the garden feature at different horizontal positions .
Identify the vertex of the function and determine the range of heights for the garden feature.
Describe the transformation applied to the basic function to obtain the given function, which reflects the design changes.
Sketch the graph of the garden feature, labeling the vertex and any intercepts.