Practice SL 2.5—Modelling functions with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
The number of bacteria in a Petri dish is modelled by the function , for , where is the number of bacteria and is the time in hours.
Find the number of bacteria in the Petri dish at .
Calculate the number of bacteria present after 10 hours.
Calculate the time, in hours, for the number of bacteria to reach .
A hot winter soup has just been removed from the stove and is left outside to cool. The soup's temperature can be modelled by the function where is the time, in minutes, since the soup was removed from the stove.
The temperature outside is .
Write down the value of and explain why it has this value.
Initially, the temperature of the soup is . Find the value of .
After two minutes, the temperature of the soup is . Find the value of .
After 15 minutes the soup is put into the fridge.
Calculate the temperature of the soup when it is put into the fridge.
In a biology lab, the population of a certain species of bacteria is observed to grow exponentially. The population in number of bacteria at time hours is modeled by the equation:
Find the initial population of the bacteria.
Determine the population after 10 hours.
Find the time required for the population to double.
Antibiotics and are applied to a pure culture of bacteria. The number of bacteria present initially for both antibiotics is 6000. The number of bacteria present for antibiotic , , can be modelled by the function , , where is the elapsed time, in hours, since the start of the experiment.
Find the value of .
The number of bacteria present for antibiotic after two hours is 2160. Find the value of . Give your answer as a fraction.
The number of bacteria present for antibiotic after four hours is 1185. The number of bacteria present for antibiotic can be modelled using a similar function to antibiotic .
Write down the function .
A company's profit per year was found to be changing at a rate of where is the company's profit in thousands of dollars and is the time since the company was founded, measured in years.
Determine whether the profit is increasing or decreasing when .
One year after the company was founded, the profit was thousand dollars. Find an expression for , when .
Consider the function . The graph of is shown in the diagram. The vertex of the graph has coordinates . The graph intersects the x-axis at two points, and .
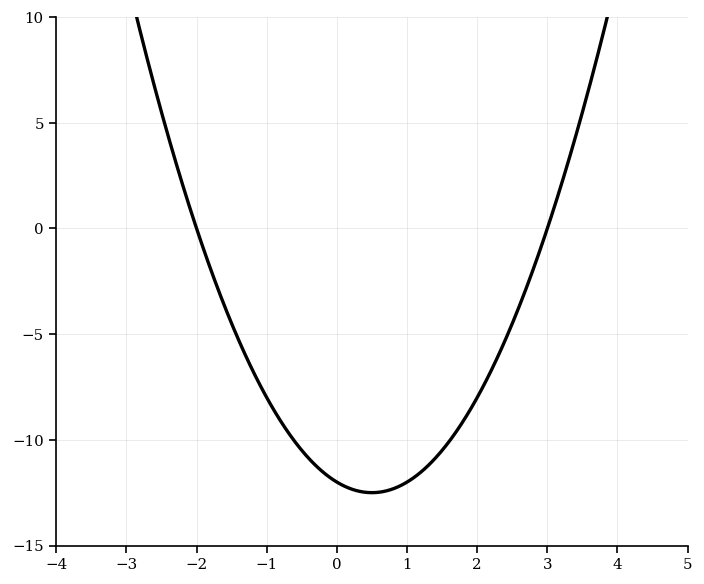
Find the value of .
Find the value of .
Find the value of .
Find the value of .
Rosa joins a club to prepare to run a marathon. During the first training session Rosa runs a distance of 3000 metres. Each training session she increases the distance she runs by 400 metres.
A marathon is 42.195 kilometres.
In the th training session Rosa will run further than a marathon for the first time.
Carlos joins the club to lose weight. He runs 7500 metres during the first month. The distance he runs increases by 20% each month.
Write down the distance Rosa runs in the third training session.
Find the value of .
Calculate the total distance, in kilometres, Rosa runs in the first 50 training sessions.
Calculate the total distance Carlos runs in the first year.
Find the distance Carlos runs in the fifth month of training.
Write down the distance Rosa runs in the th training session.
The depth of water in a port is modelled by the function $d(t) = p\cos qt + 7.5$, for $0 \leqslant t \leqslant 12$, where $t$ is the number of hours after high tide.
At high tide, the depth is 9.7 metres.
At low tide, which is 7 hours later, the depth is 5.3 metres.
Find the value of $p$.
Find the value of $q$.
Use the model to find the depth of the water 10 hours after high tide.
The strength of earthquakes is measured on the Richter magnitude scale, with values typically between $0$ and $8$ where $8$ is the most severe.
The Gutenberg–Richter equation gives the average number of earthquakes per year, $N$, which have a magnitude of at least $M$. For a particular region the equation is
$$ \log_{10} N = a - M \text{, for some } a \in \mathbb{R} $$This region has an average of $100$ earthquakes per year with a magnitude of at least $3$.
The equation for this region can also be written as $N = \frac{b}{10^M}$.
The expected length of time, in years, between earthquakes with a magnitude of at least $M$ is $\frac{1}{N}$.
Within this region the most severe earthquake recorded had a magnitude of $7.2$.
Find the value of $a$.
Find the value of $b$.
Given $0 < M < 8$, find the range for $N$.
Find the expected length of time between this earthquake and the next earthquake of at least this magnitude. Give your answer to the nearest year.
The amount, in milligrams, of a medicinal drug in the body hours after it was injected is given by . Before this injection, the amount of the drug in the body was zero.
Write down the initial dose of the drug.
Write down the percentage of the drug that leaves the body each hour.
Calculate the amount of the drug remaining in the body 10 hours after the injection.