- IB
- AHL 2.8—Transformations of graphs, composite transformations
Practice AHL 2.8—Transformations of graphs, composite transformations with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
The point lies on the curve . Write down the coordinates of the corresponding point under the following transformations.
A city planner is analyzing the function representing the cost of public transportation, given by
This function is transformed to produce various other functions.
Write down the equation of if it represents reflected in the -axis.
Write down the equation of if it represents reflected in the -axis.
Describe the transformations applied to to obtain .
The point lies on the curve .
Find the coordinates of the corresponding point under .
A local community is developing a new park and wants to model the height of a parabolic fountain using the quadratic function . The fountain reaches its maximum height of 5 meters when positioned at meters from the base.
Determine the values of and that define this fountain's height.
If the fountain's design is modified to shift it 3 meters to the right, calculate the equation of the new height function.
A financial analyst is examining the natural logarithm function to model investment growth, given by .
Write the equation of the function after a vertical stretch of by a factor of 14.
Write the equation of the function after a horizontal shrink of by a factor of 3.
Describe the domain and range of the transformed function .
The quadratic function is defined by .
On the following grid, draw the graph of for .
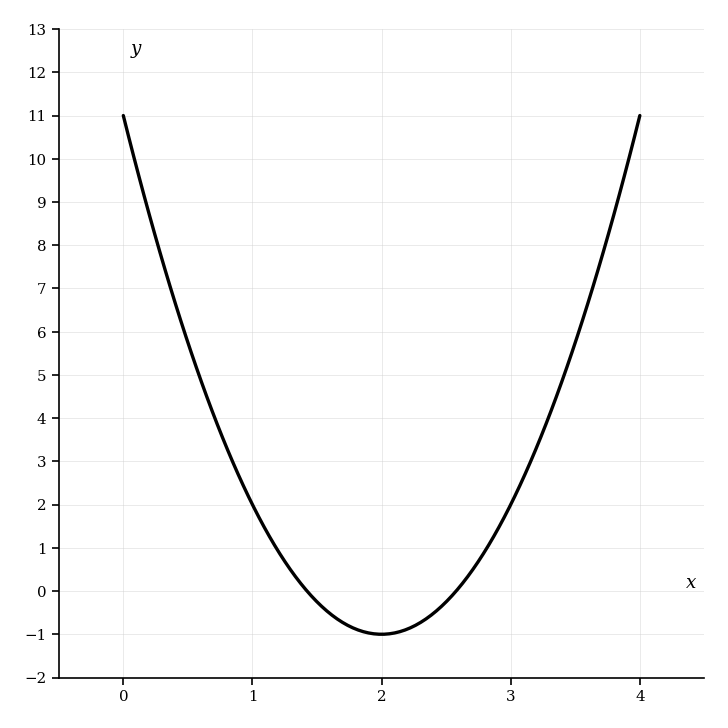
Write function in the form .
The graph of is translated 3 units in the positive -direction and 5 units in the positive -direction. Find the function for the translated graph, giving your answer in the form .
Let . Part of the graph of is shown below.
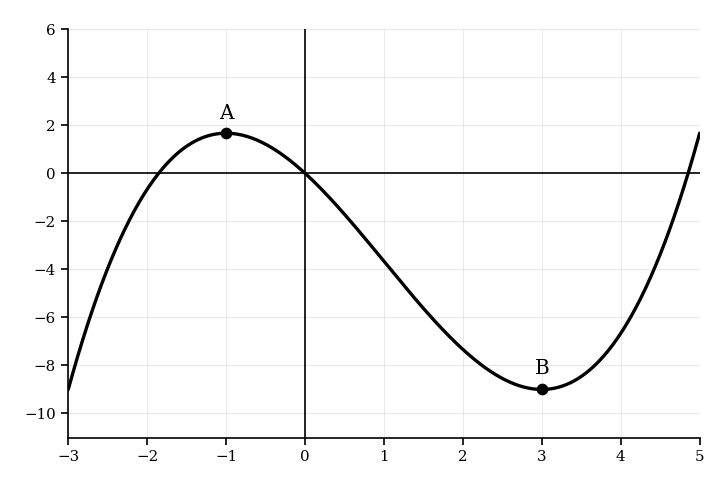
The graph has a maximum point at and a minimum point at . Write down the coordinates of:
the image of after reflection in the -axis.
the image of after translation by the vector .
the image of after reflection in the -axis followed by a horizontal stretch with scale factor .
Let . The graph of is translated 1 unit to the right and 2 units down.
The graph of is the image of the graph of after this translation.
Write down the coordinates of the vertex of the graph of .
Express in the form .
The graph of is reflected in the -axis to give the graph of . Write down the coordinates of the vertex of the graph of .
At an archery tournament, a particular competition sees a ball launched into the air while an archer attempts to hit it with an arrow. The path of the ball is modelled by the equation where is the horizontal displacement from the archer and is the vertical displacement from the ground, both measured in metres, and is the time, in seconds, since the ball was launched.
Find the initial speed of the ball.
Find the angle of elevation of the ball as it is launched.
Find the maximum height reached by the ball.
Assuming that the ground is horizontal and the ball is not hit by the arrow, find the coordinate of the point where the ball lands.
For the path of the ball, find an expression for in terms of .
An archer releases an arrow from the point (0, 2). The arrow is modelled as travelling in a straight line, in the same plane as the ball, with speed 60 m s⁻¹ and an angle of elevation of 10°. Determine the two positions where the path of the arrow intersects the path of the ball.
Determine the time when the arrow should be released to hit the ball before the ball reaches its maximum height.
Let the function .
Draw the graph of for .
Let . Draw the graph of for .
Practice AHL 2.8—Transformations of graphs, composite transformations with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
The point lies on the curve . Write down the coordinates of the corresponding point under the following transformations.
A city planner is analyzing the function representing the cost of public transportation, given by
This function is transformed to produce various other functions.
Write down the equation of if it represents reflected in the -axis.
Write down the equation of if it represents reflected in the -axis.
Describe the transformations applied to to obtain .
The point lies on the curve .
Find the coordinates of the corresponding point under .
A local community is developing a new park and wants to model the height of a parabolic fountain using the quadratic function . The fountain reaches its maximum height of 5 meters when positioned at meters from the base.
Determine the values of and that define this fountain's height.
If the fountain's design is modified to shift it 3 meters to the right, calculate the equation of the new height function.
A financial analyst is examining the natural logarithm function to model investment growth, given by .
Write the equation of the function after a vertical stretch of by a factor of 14.
Write the equation of the function after a horizontal shrink of by a factor of 3.
Describe the domain and range of the transformed function .
The quadratic function is defined by .
On the following grid, draw the graph of for .

Write function in the form .
The graph of is translated 3 units in the positive -direction and 5 units in the positive -direction. Find the function for the translated graph, giving your answer in the form .
Let . Part of the graph of is shown below.

The graph has a maximum point at and a minimum point at . Write down the coordinates of:
the image of after reflection in the -axis.
the image of after translation by the vector .
the image of after reflection in the -axis followed by a horizontal stretch with scale factor .
Let . The graph of is translated 1 unit to the right and 2 units down.
The graph of is the image of the graph of after this translation.
Write down the coordinates of the vertex of the graph of .
Express in the form .
The graph of is reflected in the -axis to give the graph of . Write down the coordinates of the vertex of the graph of .
At an archery tournament, a particular competition sees a ball launched into the air while an archer attempts to hit it with an arrow. The path of the ball is modelled by the equation where is the horizontal displacement from the archer and is the vertical displacement from the ground, both measured in metres, and is the time, in seconds, since the ball was launched.
Find the initial speed of the ball.
Find the angle of elevation of the ball as it is launched.
Find the maximum height reached by the ball.
Assuming that the ground is horizontal and the ball is not hit by the arrow, find the coordinate of the point where the ball lands.
For the path of the ball, find an expression for in terms of .
An archer releases an arrow from the point (0, 2). The arrow is modelled as travelling in a straight line, in the same plane as the ball, with speed 60 m s⁻¹ and an angle of elevation of 10°. Determine the two positions where the path of the arrow intersects the path of the ball.
Determine the time when the arrow should be released to hit the ball before the ball reaches its maximum height.
Let the function .
Draw the graph of for .
Let . Draw the graph of for .