Practice SL 2.2—Functions, domains, range, graphs with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
The time taken for a chemical reaction to complete, (in seconds), depending on temperature (in degrees Celsius), is modeled by:
Find the range of the function .
Describe what happens to the time taken for the reaction to complete as the temperature increases indefinitely.
The function is defined by , .
Write down the range of .
Find an expression for .
Write down the domain and range of .
The strength of earthquakes is measured on the Richter magnitude scale, with values typically between $0$ and $8$ where $8$ is the most severe.
The Gutenberg–Richter equation gives the average number of earthquakes per year, $N$, which have a magnitude of at least $M$. For a particular region the equation is
$$ \log_{10} N = a - M \text{, for some } a \in \mathbb{R} $$This region has an average of $100$ earthquakes per year with a magnitude of at least $3$.
The equation for this region can also be written as $N = \frac{b}{10^M}$.
The expected length of time, in years, between earthquakes with a magnitude of at least $M$ is $\frac{1}{N}$.
Within this region the most severe earthquake recorded had a magnitude of $7.2$.
Find the value of $a$.
Find the value of $b$.
Given $0 < M < 8$, find the range for $N$.
Find the expected length of time between this earthquake and the next earthquake of at least this magnitude. Give your answer to the nearest year.
Let $f(x) = x^2 + 2x + 1$ and $g(x) = x - 5$, for $x \in \mathbb{R}$.
Find $(g \circ f)(x)$.
Find $f(8)$.
Solve $(g \circ f)(x) = 0$.
A function is defined by .
Find the range of .
Find an expression for the inverse function . The domain is not required.
Find the range of .
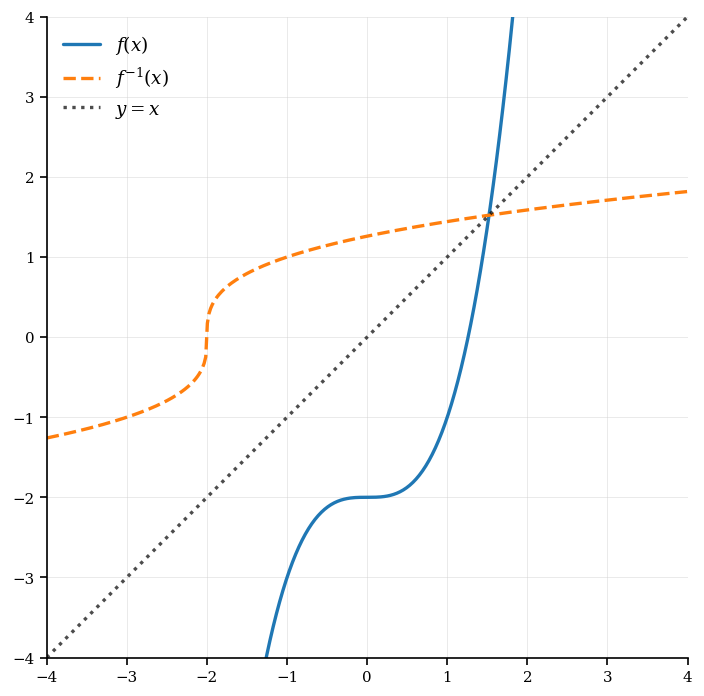
A technology company is developing a new software that predicts user engagement based on a cubic function, modeled by . They are interested in finding the inverse of this function to understand how changes in engagement levels affect user input.
Find the inverse function to determine the input value that corresponds to a specific engagement level.
Sketch the graph of , , and the line on the same axes to visualize the relationship between user engagement and input.
The graph of a quadratic function has $y$-intercept 10 and one of its $x$-intercepts is 1.
The $x$-coordinate of the vertex of the graph is 3.
The equation of the quadratic function is in the form $y = ax^2 + bx + c$.
Write down the value of $c$.
Find the value of $a$ and of $b$.
Write down the second $x$-intercept of the function.
A delivery service is testing the efficiency of a ramp for loading packages onto delivery trucks. The ramp is inclined at an angle of and is long.
Draw a diagram of the ramp showing the slope and label the vertical rise and horizontal run.
Calculate the height of the ramp at its highest point.
If a package has a mass of , find the gravitational force component acting along the ramp (using trigonometry).
If friction is introduced on the ramp, explain how the angle of the slope affects the total force needed to move the package upward.
A startup's profit (in thousands of dollars) for selling units of a product is given by:
Find the domain of the profit function.
Discuss any real-world restrictions on the number of units that can be sold.
Analyze the behavior of as and as .
Consider the function where .
Find the inverse function .
Plot both and on the same set of axes. Use a scale of 1 unit on each axis.
Draw the line on the graph and explain how and are related to this line.
Practice SL 2.2—Functions, domains, range, graphs with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
The time taken for a chemical reaction to complete, (in seconds), depending on temperature (in degrees Celsius), is modeled by:
Find the range of the function .
Describe what happens to the time taken for the reaction to complete as the temperature increases indefinitely.
The function is defined by , .
Write down the range of .
Find an expression for .
Write down the domain and range of .
The strength of earthquakes is measured on the Richter magnitude scale, with values typically between $0$ and $8$ where $8$ is the most severe.
The Gutenberg–Richter equation gives the average number of earthquakes per year, $N$, which have a magnitude of at least $M$. For a particular region the equation is
$$ \log_{10} N = a - M \text{, for some } a \in \mathbb{R} $$This region has an average of $100$ earthquakes per year with a magnitude of at least $3$.
The equation for this region can also be written as $N = \frac{b}{10^M}$.
The expected length of time, in years, between earthquakes with a magnitude of at least $M$ is $\frac{1}{N}$.
Within this region the most severe earthquake recorded had a magnitude of $7.2$.
Find the value of $a$.
Find the value of $b$.
Given $0 < M < 8$, find the range for $N$.
Find the expected length of time between this earthquake and the next earthquake of at least this magnitude. Give your answer to the nearest year.
Let $f(x) = x^2 + 2x + 1$ and $g(x) = x - 5$, for $x \in \mathbb{R}$.
Find $(g \circ f)(x)$.
Find $f(8)$.
Solve $(g \circ f)(x) = 0$.
A function is defined by .
Find the range of .
Find an expression for the inverse function . The domain is not required.
Find the range of .
A technology company is developing a new software that predicts user engagement based on a cubic function, modeled by . They are interested in finding the inverse of this function to understand how changes in engagement levels affect user input.
Find the inverse function to determine the input value that corresponds to a specific engagement level.
Sketch the graph of , , and the line on the same axes to visualize the relationship between user engagement and input.

The graph of a quadratic function has $y$-intercept 10 and one of its $x$-intercepts is 1.
The $x$-coordinate of the vertex of the graph is 3.
The equation of the quadratic function is in the form $y = ax^2 + bx + c$.
Write down the value of $c$.
Find the value of $a$ and of $b$.
Write down the second $x$-intercept of the function.
A delivery service is testing the efficiency of a ramp for loading packages onto delivery trucks. The ramp is inclined at an angle of and is long.
Draw a diagram of the ramp showing the slope and label the vertical rise and horizontal run.
Calculate the height of the ramp at its highest point.
If a package has a mass of , find the gravitational force component acting along the ramp (using trigonometry).
If friction is introduced on the ramp, explain how the angle of the slope affects the total force needed to move the package upward.
A startup's profit (in thousands of dollars) for selling units of a product is given by:
Find the domain of the profit function.
Discuss any real-world restrictions on the number of units that can be sold.
Analyze the behavior of as and as .
Consider the function where .
Find the inverse function .
Plot both and on the same set of axes. Use a scale of 1 unit on each axis.
Draw the line on the graph and explain how and are related to this line.