Practice SL 2.6—Modelling skills with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
The average temperature of a city, , in degrees Celsius, fluctuates throughout a year and can be modelled by the function where is the elapsed time, in weeks, since the start of the year. The average temperature of the city in week 4 is 27 degrees Celsius and in week 28 it is 12 degrees Celsius.
Find the value of , assuming there are 52 weeks in a year.
Write down two equations connecting and and find their values.
Calculate how many weeks of the year that they have to be careful about the food freezing. Give your answer to the nearest integer.
The front view of the edge of a water tank is drawn on a set of axes below. The edge is modelled by .

Point has coordinates , point has coordinates and point has coordinates .
Find the value of and of .
Hence, write down the equation of the quadratic function which models the edge of the water tank.
Given that 1 unit represents , find the width of the water tank when its height is .
A local bakery offers fresh baguettes for delivery. The total cost to the customer, in Euros (€), is modeled by , where is the number of baguettes ordered and includes a fixed delivery fee.
State what the value of represents.
State what the value of represents.
Write down the minimum number of baguettes that can be ordered.
Sophie has 30 Euros. Find the maximum number of baguettes Sophie can order.
Linda owns a field, represented by the shaded region . The plan view of the field is shown in the following diagram, where both axes represent distance and are measured in metres.
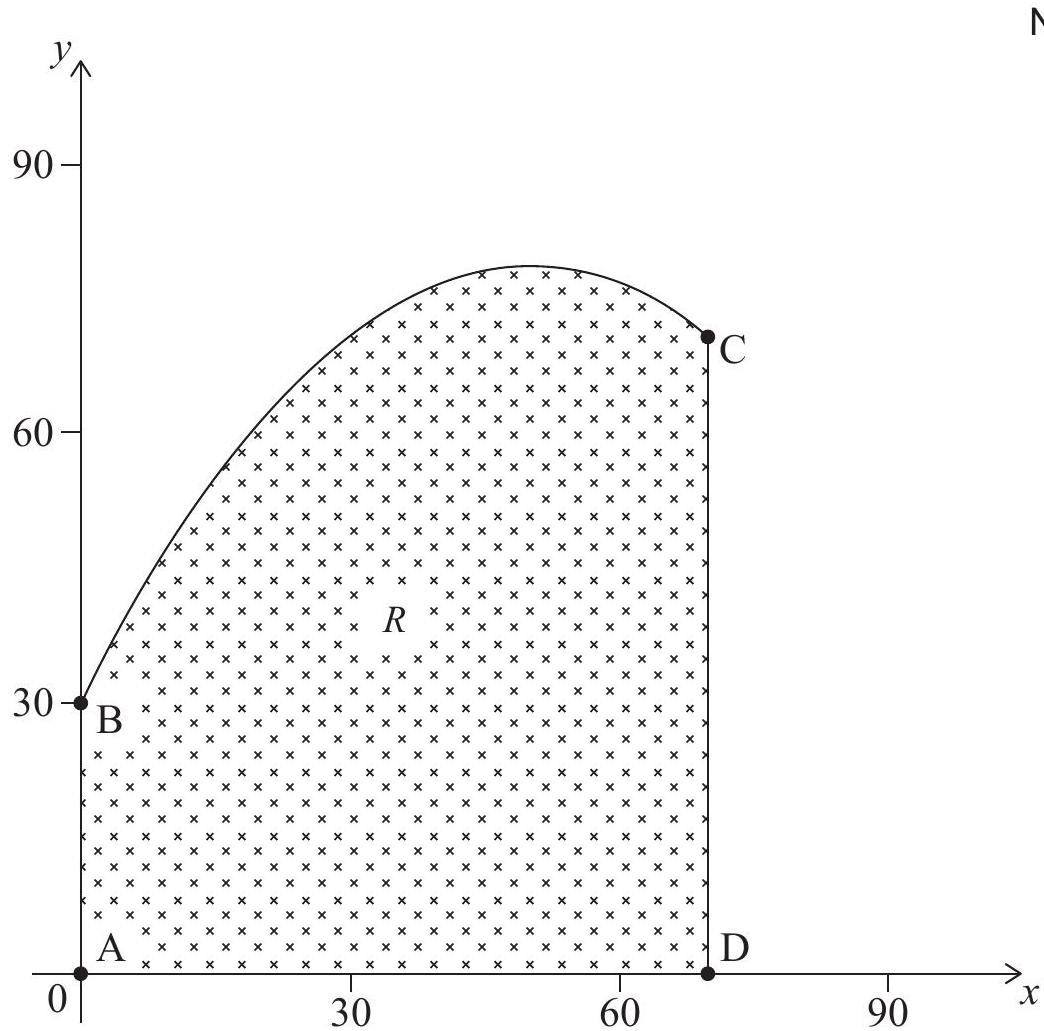
The segments , and respectively represent the western, eastern and southern boundaries of the field. The function models the northern boundary of the field between points and and is given by , for .
Find .
Hence find the coordinates of the point on the field that is furthest north.
Write down the integral which can be used to find the area of the shaded region .
Find the area of Linda's field.
Linda estimates the area of the field to be using the trapezoidal rule. Calculate the percentage error in Linda's estimate.
Suggest how Linda might be able to reduce the error whilst still using the trapezoidal rule.
A building with a square foundation is to be constructed in the field such that lies on , lies on the northern boundary, and and lie on the eastern boundary .
Find the -coordinate of point for the square foundation.
Find the area of the foundation.
A company sells cars per month for a sale price of , while incurring costs for supplies, production, and delivery of per car. Reliable market research shows that for each increase (or decrease) of the sale price by , the company will sell cars less (or more).
Find an expression for total profit, , in terms of the sale price, .
Find the values of when and explain their significance in the context of the question.
Calculate the maximum monthly profit, giving your answer to the nearest dollar.
Calculate the sale price needed to generate the maximum monthly profit.
Calculate the number of cars sold to generate the maximum monthly profit.
Olava’s Pizza Company supplies and delivers large cheese pizzas. The total cost to the customer, , in Papua New Guinean Kina (PGK), is modelled by the function: where is the number of large cheese pizzas ordered. This total cost includes a fixed cost for delivery.
State, in the context of the question, what the value of represents.
State, in the context of the question, what the value of represents.
Write down the minimum number of pizzas that can be ordered.
Kaelani has PGK. Find the maximum number of large cheese pizzas that Kaelani can order from Olava’s Pizza Company.
Algae in a lake can grow exponentially until the lake is fully covered in algae.
Find the number of days it takes for a lake to be fully covered in algae when of the lake is covered today and the covered area doubles once every five days.
In memory of the legendary musician Alex Star, tribute concerts continue to attract fans worldwide, decades after his passing in 1985. The number of attendees at these concerts, , can be modeled by
where is the number of years since 1985.
Calculate the time taken for the number of attendees to reach 100,000.
Write down the number of attendees in the year 1985.
Calculate the number of attendees when .
If the global population in 2060 is projected to be 10 billion, explain why this model for the number of attendees might be unrealistic.
Deserts are known for having high daily temperature ranges. Erica monitors the temperature, in , on a particular day in a desert. The table below shows some of the information she recorded.
| Temperature | Time | |
|---|---|---|
| Maximum | ||
| Minimum | 2:00 am |
Erica uses her observations to form the following model for the temperature, , during the day: where is the elapsed time, in hours, since midnight.
Calculate the value of when the maximum temperature occurs and fill in the time in the table above in am/pm format.
Find the value of , , and .
Erica goes exploring in the desert at 6:30 am and leaves once the temperature reaches .
Calculate the temperature range Erica experiences whilst in the desert.
Two schools are represented by points and on the graph below. A road, represented by the line with equation , passes near the schools. An architect is asked to determine the location of a new bus stop on the road such that it is the same distance from the two schools.
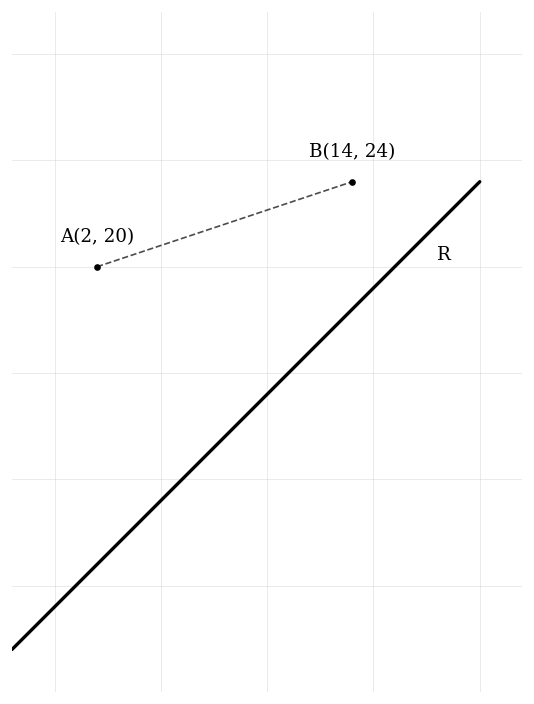
Find the equation of the perpendicular bisector of . Give your equation in the form .
Determine the coordinates of the point on where the bus stop should be located.
Practice SL 2.6—Modelling skills with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
The average temperature of a city, , in degrees Celsius, fluctuates throughout a year and can be modelled by the function where is the elapsed time, in weeks, since the start of the year. The average temperature of the city in week 4 is 27 degrees Celsius and in week 28 it is 12 degrees Celsius.
Find the value of , assuming there are 52 weeks in a year.
Write down two equations connecting and and find their values.
Calculate how many weeks of the year that they have to be careful about the food freezing. Give your answer to the nearest integer.
The front view of the edge of a water tank is drawn on a set of axes below. The edge is modelled by .

Point has coordinates , point has coordinates and point has coordinates .
Find the value of and of .
Hence, write down the equation of the quadratic function which models the edge of the water tank.
Given that 1 unit represents , find the width of the water tank when its height is .
A local bakery offers fresh baguettes for delivery. The total cost to the customer, in Euros (€), is modeled by , where is the number of baguettes ordered and includes a fixed delivery fee.
State what the value of represents.
State what the value of represents.
Write down the minimum number of baguettes that can be ordered.
Sophie has 30 Euros. Find the maximum number of baguettes Sophie can order.
Linda owns a field, represented by the shaded region . The plan view of the field is shown in the following diagram, where both axes represent distance and are measured in metres.

The segments , and respectively represent the western, eastern and southern boundaries of the field. The function models the northern boundary of the field between points and and is given by , for .
Find .
Hence find the coordinates of the point on the field that is furthest north.
Write down the integral which can be used to find the area of the shaded region .
Find the area of Linda's field.
Linda estimates the area of the field to be using the trapezoidal rule. Calculate the percentage error in Linda's estimate.
Suggest how Linda might be able to reduce the error whilst still using the trapezoidal rule.
A building with a square foundation is to be constructed in the field such that lies on , lies on the northern boundary, and and lie on the eastern boundary .
Find the -coordinate of point for the square foundation.
Find the area of the foundation.
A company sells cars per month for a sale price of , while incurring costs for supplies, production, and delivery of per car. Reliable market research shows that for each increase (or decrease) of the sale price by , the company will sell cars less (or more).
Find an expression for total profit, , in terms of the sale price, .
Find the values of when and explain their significance in the context of the question.
Calculate the maximum monthly profit, giving your answer to the nearest dollar.
Calculate the sale price needed to generate the maximum monthly profit.
Calculate the number of cars sold to generate the maximum monthly profit.
Olava’s Pizza Company supplies and delivers large cheese pizzas. The total cost to the customer, , in Papua New Guinean Kina (PGK), is modelled by the function: where is the number of large cheese pizzas ordered. This total cost includes a fixed cost for delivery.
State, in the context of the question, what the value of represents.
State, in the context of the question, what the value of represents.
Write down the minimum number of pizzas that can be ordered.
Kaelani has PGK. Find the maximum number of large cheese pizzas that Kaelani can order from Olava’s Pizza Company.
Algae in a lake can grow exponentially until the lake is fully covered in algae.
Find the number of days it takes for a lake to be fully covered in algae when of the lake is covered today and the covered area doubles once every five days.
In memory of the legendary musician Alex Star, tribute concerts continue to attract fans worldwide, decades after his passing in 1985. The number of attendees at these concerts, , can be modeled by
where is the number of years since 1985.
Calculate the time taken for the number of attendees to reach 100,000.
Write down the number of attendees in the year 1985.
Calculate the number of attendees when .
If the global population in 2060 is projected to be 10 billion, explain why this model for the number of attendees might be unrealistic.
Deserts are known for having high daily temperature ranges. Erica monitors the temperature, in , on a particular day in a desert. The table below shows some of the information she recorded.
| Temperature | Time | |
|---|---|---|
| Maximum | ||
| Minimum | 2:00 am |
Erica uses her observations to form the following model for the temperature, , during the day: where is the elapsed time, in hours, since midnight.
Calculate the value of when the maximum temperature occurs and fill in the time in the table above in am/pm format.
Find the value of , , and .
Erica goes exploring in the desert at 6:30 am and leaves once the temperature reaches .
Calculate the temperature range Erica experiences whilst in the desert.
Two schools are represented by points and on the graph below. A road, represented by the line with equation , passes near the schools. An architect is asked to determine the location of a new bus stop on the road such that it is the same distance from the two schools.

Find the equation of the perpendicular bisector of . Give your equation in the form .
Determine the coordinates of the point on where the bus stop should be located.