Practice SL 4.7—Discrete random variables with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
John likes to go sailing every day in July. To help him make a decision on whether it is safe to go sailing he classifies each day in July as windy or calm. Given that a day in July is calm, the probability that the next day is calm is $0.9$. Given that a day in July is windy, the probability that the next day is calm is $0.3$. The weather forecast for the 1st July predicts that the probability that it will be calm is $0.8$.
Draw a tree diagram to represent this information for the first three days of July.
Find the probability that the 3rd July is calm.
Find the probability that the 1st July was calm given that the 3rd July is windy.
A Chocolate Shop advertises free gifts to customers that collect three vouchers. The vouchers are placed at random into 10% of all chocolate bars sold at this shop. Kati buys some of these bars and she opens them one at a time to see if they contain a voucher. Let $\text{P}(X = n)$ be the probability that Kati obtains her third voucher on the $n$th bar opened.
(It is assumed that the probability that a chocolate bar contains a voucher stays at 10% throughout the question.)
It is given that $\text{P}(X = n) = \frac{n^2 + an + b}{2000} \times 0.9^{n - 3}$ for $n \geqslant 3, n \in \mathbb{N}$.
Kati’s mother goes to the shop and buys $x$ chocolate bars. She takes the bars home for Kati to open.
Show that $\text{P}(X = 3) = 0.001$ and $\text{P}(X = 4) = 0.0027$.
Find the values of the constants $a$ and $b$.
Deduce that $\frac{\text{P}(X = n)}{\text{P}(X = n - 1)} = \frac{0.9(n - 1)}{n - 3}$ for $n > 3$.
(i) Hence show that $X$ has two modes $m_1$ and $m_2$.
(ii) State the values of $m_1$ and $m_2$.
Determine the minimum value of $x$ such that the probability Kati receives at least one free gift is greater than 0.5.
Mr Burke teaches a mathematics class with 15 students. In this class there are 6 female students and 9 male students.
Each day Mr Burke randomly chooses one student to answer a homework question.
In the first month, Mr Burke will teach his class 20 times.
Find the probability that on any given day Mr Burke chooses a female student to answer a question.
Find the probability he will choose a female student 8 times.
Find the probability he will choose a male student at most 9 times.
In a city, of people have blue eyes. If someone has blue eyes, the probability that they also have fair hair is . This information is represented in the following tree diagram.
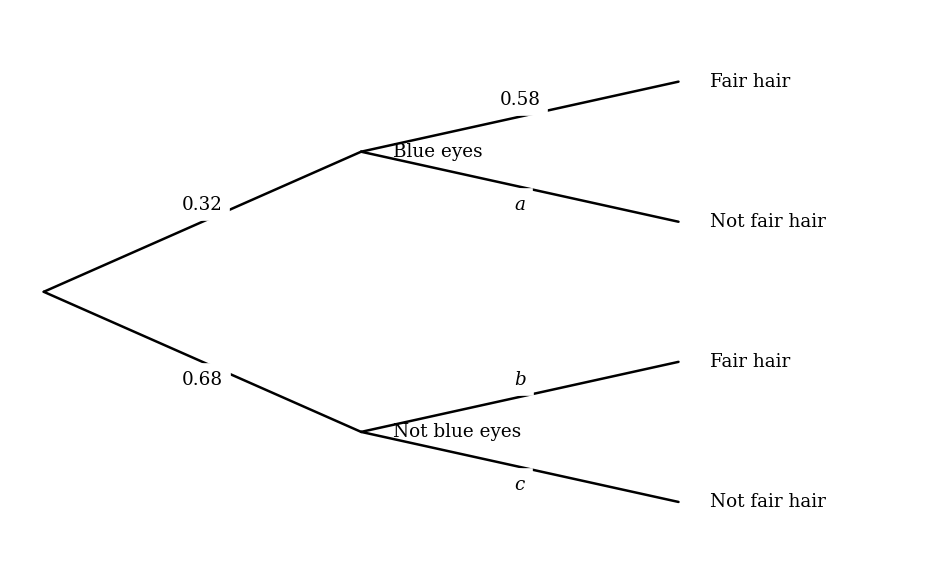
It is known that of people in this city have fair hair.
Write down the value of .
Find an expression, in terms of , for the probability of a person not having blue eyes and having fair hair.
Calculate the value of .
Calculate the value of .
At Mirabooka Primary School, a survey found that 68% of students have a dog and 36% of students have a cat. 14% of students have both a dog and a cat. This information can be represented in the following Venn diagram, where m, n, p and q represent the percentage of students within each region. 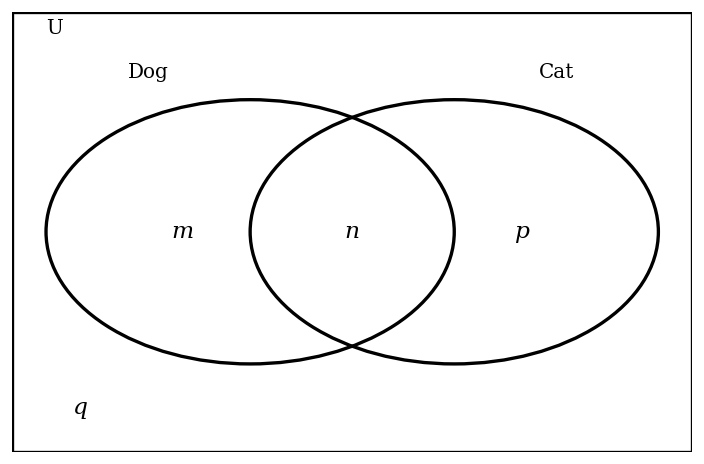
Find the value of m.
Find the value of n.
Find the value of p.
Find the value of q.
Find the probability that a randomly chosen student has a dog but does not have a cat.
Find the probability that a randomly chosen student has a dog given that they do not have a cat.
Tim models the number of school captains appointed in the next 10 years who have a dog using a binomial distribution. Assume one school captain is appointed each year. Use Tim's model to find the probability that in the next 10 years 5 school captains have a dog.
Use Tim's model to find the probability that in the next 10 years more than 3 school captains have a dog.
Use Tim's model to find the probability that in the next 10 years exactly 9 school captains in succession have a dog.
State why Tim should not use the binomial distribution to find the probability that 5 school captains have a dog.
A manufacturer produces 1500 boxes of breakfast cereal every day.
The weights of these boxes are normally distributed with a mean of 502 grams and a standard deviation of 2 grams.
All boxes of cereal with a weight between 497.5 grams and 505 grams are sold. The manufacturer’s income from the sale of each box of cereal is $2.00.
The manufacturer recycles any box of cereal with a weight not between 497.5 grams and 505 grams. The manufacturer’s recycling cost is $0.16 per box.
A different manufacturer produces boxes of cereal with weights that are normally distributed with a mean of 350 grams and a standard deviation of 1.8 grams.
This manufacturer sells all boxes of cereal that are above a minimum weight, $w$.
They sell 97% of the cereal boxes produced.
Calculate the manufacturer’s expected daily recycling cost.
(i) Find the probability that a box of cereal, chosen at random, is sold.
(ii) Calculate the manufacturer’s expected daily income from these sales.
Calculate the value of $w$.
Mr Burke teaches a mathematics class with 15 students. In this class there are 6 female students and 9 male students.
Each day Mr Burke randomly chooses one student to answer a homework question.
In the first month, Mr Burke will teach his class 20 times.
Find the probability he will choose a female student 8 times.
The Head of Year, Mrs Smith, decides to select a student at random from the year group to read the notices in assembly. There are 80 students in total in the year group. Mrs Smith calculates the probability of picking a male student 8 times in the first 20 assemblies is 0.153357 correct to 6 decimal places.
Find the number of male students in the year group.
In a large university the probability that a student is left handed is 0.08. A sample of 150 students is randomly selected from the university. Let $k$ be the expected number of left-handed students in this sample.
Find $k$.
Hence, find the probability that exactly $k$ students are left handed.
Hence, find the probability that fewer than $k$ students are left handed.
A group of 130 applicants applied for admission into either the Arts programme or the Sciences programme at a university. The outcomes of their applications are shown in the following table.
| Accepted | Rejected | |
|---|---|---|
| Arts programme | 17 | 24 |
| Sciences programme | 25 | 64 |
Find the probability that a randomly chosen applicant from this group was accepted by the university.
An applicant is chosen at random from this group. It is found that they were accepted into the programme of their choice. Find the probability that the applicant applied for the Arts programme.
Two different applicants are chosen at random from the original group. Find the probability that both applicants applied to the Arts programme.
The Home Shine factory produces light bulbs, of which are found to be defective.
Francesco buys two light bulbs produced by Home Shine.
The Bright Light factory also produces light bulbs. The probability that a light bulb produced by Bright Light is not defective is .
Deborah buys three light bulbs produced by Bright Light.
Write down the probability that a light bulb produced by Home Shine is not defective.
Find the probability that both light bulbs are not defective.
Find the probability that at least one of Francesco’s light bulbs is defective.
Write down an expression, in terms of , for the probability that at least one of Deborah’s three light bulbs is defective.
Practice SL 4.7—Discrete random variables with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
John likes to go sailing every day in July. To help him make a decision on whether it is safe to go sailing he classifies each day in July as windy or calm. Given that a day in July is calm, the probability that the next day is calm is $0.9$. Given that a day in July is windy, the probability that the next day is calm is $0.3$. The weather forecast for the 1st July predicts that the probability that it will be calm is $0.8$.
Draw a tree diagram to represent this information for the first three days of July.
Find the probability that the 3rd July is calm.
Find the probability that the 1st July was calm given that the 3rd July is windy.
A Chocolate Shop advertises free gifts to customers that collect three vouchers. The vouchers are placed at random into 10% of all chocolate bars sold at this shop. Kati buys some of these bars and she opens them one at a time to see if they contain a voucher. Let $\text{P}(X = n)$ be the probability that Kati obtains her third voucher on the $n$th bar opened.
(It is assumed that the probability that a chocolate bar contains a voucher stays at 10% throughout the question.)
It is given that $\text{P}(X = n) = \frac{n^2 + an + b}{2000} \times 0.9^{n - 3}$ for $n \geqslant 3, n \in \mathbb{N}$.
Kati’s mother goes to the shop and buys $x$ chocolate bars. She takes the bars home for Kati to open.
Show that $\text{P}(X = 3) = 0.001$ and $\text{P}(X = 4) = 0.0027$.
Find the values of the constants $a$ and $b$.
Deduce that $\frac{\text{P}(X = n)}{\text{P}(X = n - 1)} = \frac{0.9(n - 1)}{n - 3}$ for $n > 3$.
(i) Hence show that $X$ has two modes $m_1$ and $m_2$.
(ii) State the values of $m_1$ and $m_2$.
Determine the minimum value of $x$ such that the probability Kati receives at least one free gift is greater than 0.5.
Mr Burke teaches a mathematics class with 15 students. In this class there are 6 female students and 9 male students.
Each day Mr Burke randomly chooses one student to answer a homework question.
In the first month, Mr Burke will teach his class 20 times.
Find the probability that on any given day Mr Burke chooses a female student to answer a question.
Find the probability he will choose a female student 8 times.
Find the probability he will choose a male student at most 9 times.
In a city, of people have blue eyes. If someone has blue eyes, the probability that they also have fair hair is . This information is represented in the following tree diagram.

It is known that of people in this city have fair hair.
Write down the value of .
Find an expression, in terms of , for the probability of a person not having blue eyes and having fair hair.
Calculate the value of .
Calculate the value of .
At Mirabooka Primary School, a survey found that 68% of students have a dog and 36% of students have a cat. 14% of students have both a dog and a cat. This information can be represented in the following Venn diagram, where m, n, p and q represent the percentage of students within each region. 
Find the value of m.
Find the value of n.
Find the value of p.
Find the value of q.
Find the probability that a randomly chosen student has a dog but does not have a cat.
Find the probability that a randomly chosen student has a dog given that they do not have a cat.
Tim models the number of school captains appointed in the next 10 years who have a dog using a binomial distribution. Assume one school captain is appointed each year. Use Tim's model to find the probability that in the next 10 years 5 school captains have a dog.
Use Tim's model to find the probability that in the next 10 years more than 3 school captains have a dog.
Use Tim's model to find the probability that in the next 10 years exactly 9 school captains in succession have a dog.
State why Tim should not use the binomial distribution to find the probability that 5 school captains have a dog.
A manufacturer produces 1500 boxes of breakfast cereal every day.
The weights of these boxes are normally distributed with a mean of 502 grams and a standard deviation of 2 grams.
All boxes of cereal with a weight between 497.5 grams and 505 grams are sold. The manufacturer’s income from the sale of each box of cereal is $2.00.
The manufacturer recycles any box of cereal with a weight not between 497.5 grams and 505 grams. The manufacturer’s recycling cost is $0.16 per box.
A different manufacturer produces boxes of cereal with weights that are normally distributed with a mean of 350 grams and a standard deviation of 1.8 grams.
This manufacturer sells all boxes of cereal that are above a minimum weight, $w$.
They sell 97% of the cereal boxes produced.
Calculate the manufacturer’s expected daily recycling cost.
(i) Find the probability that a box of cereal, chosen at random, is sold.
(ii) Calculate the manufacturer’s expected daily income from these sales.
Calculate the value of $w$.
Mr Burke teaches a mathematics class with 15 students. In this class there are 6 female students and 9 male students.
Each day Mr Burke randomly chooses one student to answer a homework question.
In the first month, Mr Burke will teach his class 20 times.
Find the probability he will choose a female student 8 times.
The Head of Year, Mrs Smith, decides to select a student at random from the year group to read the notices in assembly. There are 80 students in total in the year group. Mrs Smith calculates the probability of picking a male student 8 times in the first 20 assemblies is 0.153357 correct to 6 decimal places.
Find the number of male students in the year group.
In a large university the probability that a student is left handed is 0.08. A sample of 150 students is randomly selected from the university. Let $k$ be the expected number of left-handed students in this sample.
Find $k$.
Hence, find the probability that exactly $k$ students are left handed.
Hence, find the probability that fewer than $k$ students are left handed.
A group of 130 applicants applied for admission into either the Arts programme or the Sciences programme at a university. The outcomes of their applications are shown in the following table.
| Accepted | Rejected | |
|---|---|---|
| Arts programme | 17 | 24 |
| Sciences programme | 25 | 64 |
Find the probability that a randomly chosen applicant from this group was accepted by the university.
An applicant is chosen at random from this group. It is found that they were accepted into the programme of their choice. Find the probability that the applicant applied for the Arts programme.
Two different applicants are chosen at random from the original group. Find the probability that both applicants applied to the Arts programme.
The Home Shine factory produces light bulbs, of which are found to be defective.
Francesco buys two light bulbs produced by Home Shine.
The Bright Light factory also produces light bulbs. The probability that a light bulb produced by Bright Light is not defective is .
Deborah buys three light bulbs produced by Bright Light.
Write down the probability that a light bulb produced by Home Shine is not defective.
Find the probability that both light bulbs are not defective.
Find the probability that at least one of Francesco’s light bulbs is defective.
Write down an expression, in terms of , for the probability that at least one of Deborah’s three light bulbs is defective.