RevisionDojo

AHL 4.13—Non-linear regression - IB Questionbank | RevisionDojo

Practice AHL 4.13—Non-linear regression with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.

Paper

Level

Question 1

HLPaper 2

A biologist is studying the growth of a bacterial colony. The number of bacteria, $B$ (in thousands), after $t$ hours is recorded as follows:

$t$	0	2	4	6
$B$	1.0	2.2	4.8	10.5

The biologist models the growth using a logistic function of the form $B=\frac{L}{1+C e^{-k t}}$ , where $L, C$ , and $k$ are positive constants, and $L$ represents the carrying capacity.

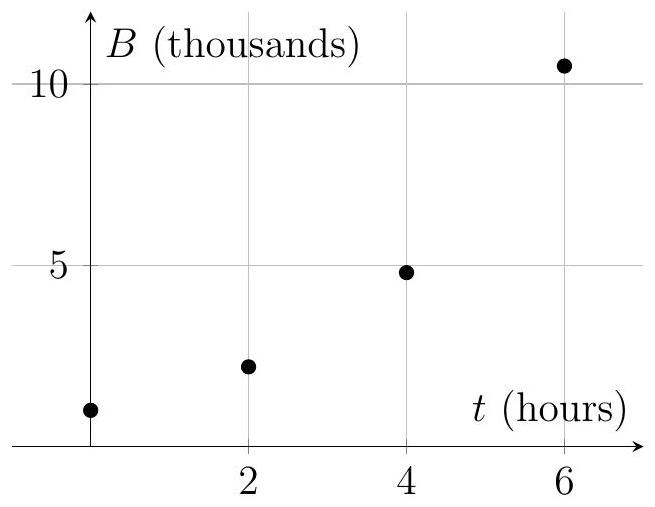
Explain why a logistic model is appropriate for this data.

[1]

Transform the logistic model into a linear form to estimate parameters using regression.

[2]

Estimate $L, C$ , and $k$ using the data provided.

[3]

Predict the number of bacteria after 8 hours.

[2]

Discuss one limitation of using this logistic model for long-term predictions.

[1]

Question 2

HLPaper 1

Elena is modeling the decay of a radioactive substance. The mass, $M$ (in grams), remaining after $t$ days is given by:

$t$	0	5	10	15
$M$	100	60.7	36.8	22.3

She proposes a model of the form $M=M_{0} e^{-k t}$ , where $M_{0}$ and $k$ are positive constants.

Show that the model satisfies the differential equation $\frac{d M}{d t}=-k M$ .

[2]

Find the values of $M_{0}$ and $k$ using a logarithmic transformation and least squares regression.

[3]

Estimate the mass remaining after 20 days.

[2]

Calculate the sum of squared residuals for the model at the given data points.

[2]

Question 3

HLPaper 1

A marine biologist models the oxygen concentration, $C$ (in $\mathrm{mg} / \mathrm{L}$ ), in a coral reef as a function of time, $t$ (in hours), over a 24 -hour period. The data suggests a sinusoidal pattern:

$t$	0	6	12	18	24
$C$	6.0	7.5	6.0	4.5	6.0

The biologist proposes a model of the form $C=a \sin (b t)+d$ , where $a, b$ , and $d$ are constants.

Show that the period of the proposed model is $\frac{2 \pi}{b}$ .

[2]

Given the data suggests a 24 -hour period, find the value of $b$ .

[2]

Find the values of $a$ and $d$ using least squares regression.

[3]

Calculate the sum of squared residuals for the model at the given points.

[2]

Discuss one limitation of this model for predicting oxygen levels beyond 24 hours.

[1]

Question 4

HLPaper 2

An ecologist models the population density of a species, $D$ (in individuals per $\mathrm{km}^{2}$ ), as a function of distance, $x$ (in km), from a pollution source. The data suggests a Gaussian distribution:

$x$	0	1	2	3
$D$	10	50	80	50

The ecologist proposes a model of the form $D=a e^{-b(x-c)^{2}}$ , where $a, b$ , and $c$ are constants.

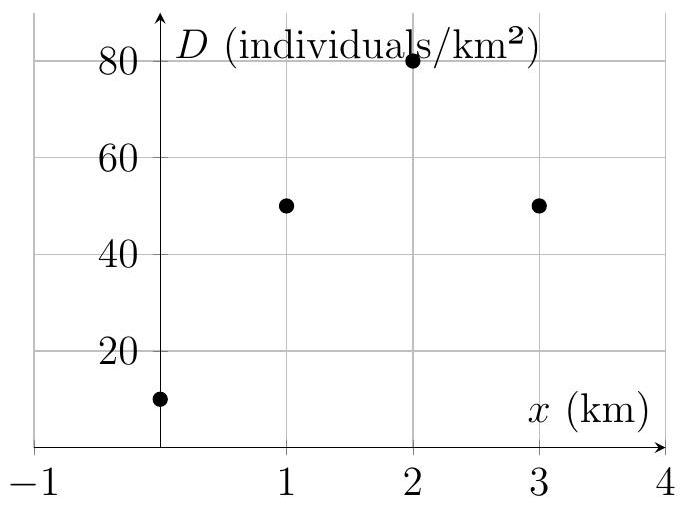
Transform the model into a linear form for regression.

[2]

Estimate $a, b$ , and $c$ using least squares regression.

[3]

Calculate the coefficient of determination, $R^{2}$ , for the model.

[2]

Predict the population density at $x=4 \mathrm{~km}$ .

[2]

Discuss one limitation of this model for predicting density at large distances.

[1]

Question 5

HLPaper 1

An engineer models the vibration amplitude, $A$ (in mm), of a machine as a function of its operating frequency, $f$ (in Hz). The data suggests a polynomial relationship:

$f$	10	20	30	40
$A$	2.5	5.0	6.0	5.5

The engineer proposes a cubic model of the form $A=a f^{3}+b f^{2}+c f+d$ , where $a, b, c$ , and $d$ are constants.

Find the equation of the least squares cubic regression curve.

[3]

Write down the coefficient of determination, $R^{2}$ , for this model.

[1]

Find the frequency at which the amplitude is maximized, using the cubic model.

[3]

Calculate the sum of squared residuals for the model at the given points.

[2]

Suggest one reason why a cubic model might not be appropriate for frequencies far beyond 40 Hz .

[1]

Question 6

HLPaper 1

A physicist investigates the cooling of a metal rod after being removed from a furnace. The temperature, $T$ (in ${ }^{\circ} \mathrm{C}$ ), of the rod at time $t$ (in minutes) is recorded as:

$t$	0	5	10	15
$T$	200	150	120	100

The physicist proposes a modified exponential model of the form $T=a e^{-k t}+T_{0}$ , where $a, k$ , and $T_{0}$ are constants, and $T_{0}$ represents the ambient temperature (assumed to be $20^{\circ} \mathrm{C}$ ).

Show that $T-T_{0}$ follows an exponential decay model.

[2]

Find the values of $a$ and $k$ using least squares regression, given $T_{0}=20$ .

[3]

Calculate the sum of squared residuals for the model.

[2]

Predict the temperature after 20 minutes.

[2]

Question 7

HLPaper 1

A researcher studies the intensity of light, $I$ (in lumens), emitted by a bioluminescent organism as a function of time, $t$ (in hours), after exposure to a stimulus. The data is:

$t$	0	1	2	3
$I$	50	45	35	25

The researcher proposes a model of the form $I=a e^{-k t}+b$ , where $a, k$ , and $b$ are constants, and $b$ represents the baseline intensity.

Show that $I-b$ follows an exponential decay model.

[2]

Given $b=20$ , find the values of $a$ and $k$ using least squares regression.

[3]

Calculate the sum of squared residuals for the model.

[2]

Estimate the light intensity after 4 hours.

[2]

Question 8

HLPaper 2

An engineer studies the relationship between the speed, $s$ (in $\mathrm{m} / \mathrm{s}$ ), of a conveyor belt and the power consumption, $P$ (in watts), of the motor. The data is:

$s$	1	2	3	4
$P$	500	650	900	1300

The engineer proposes a rational model of the form $P=\frac{a}{s+b}+c$ , where $a, b$ , and $c$ are constants.

Transform the model into a linear form for regression.

[2]

Find the values of $a, b$ , and $c$ using least squares regression.

[3]

Calculate the coefficient of determination, $R^{2}$ , for the model.

[2]

Estimate the power consumption at a speed of $5 \mathrm{~m} / \mathrm{s}$ .

[2]

Explain one potential issue with this model for very low speeds.

[1]

Question 9

HLPaper 2

Amir is studying the relationship between the time, $t$ (in weeks), since a new fitness app was launched and the number of active users, $N$ (in thousands). He collects the following data:

$t$	1	2	3	4	5
$N$	2.5	4.8	8.7	15.2	25.3

Amir believes the growth in users follows an exponential model of the form $N=A e^{k t}$ , where $A$ and $k$ are constants. To analyze this, he considers the natural logarithm of the number of users, $\ln N$ , and its relationship with time $t$ .

Find the equation of the least squares regression line for $\ln N$ against $t$ .

[2]

Using the model from part (a), estimate the number of active users after 6 weeks.

[3]

Calculate the coefficient of determination, $R^{2}$ , for the exponential model.

[2]

Amir considers an alternative quadratic model of the form $N=a t^{2}+b t+c$ . Find the equation of the least squares regression quadratic for the given data.

[2]

Compare the suitability of the exponential and quadratic models based on their coefficients of determination.

[1]

Question 10

HLPaper 2

A city planner analyzes the relationship between the distance, $d$ (in km), from the city center and the population density, $D$ (in people per $\mathrm{km}^{2}$ ). The data is:

$d$	1	2	3	4
$D$	8000	4000	2000	1000

The planner proposes a model of the form $D=\frac{a}{d^{k}}$ , where $a$ and $k$ are positive constants.

Transform the model into a linear form for regression.

[2]

Find the values of $a$ and $k$ using least squares regression.

[3]

Calculate the coefficient of determination, $R^{2}$ , for the model.

[2]

Estimate the population density at a distance of 5 km .

[2]

Discuss one limitation of this model for predicting densities at large distances.

[1]

AHL 4.13—Non-linear regression Questionbank