RevisionDojo

SL 5.2—Increasing and decreasing functions - IB Questionbank | RevisionDojo

Practice SL 5.2—Increasing and decreasing functions with authentic IB Mathematics Analysis and Approaches (AA) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like functions and equations, calculus, complex numbers, sequences and series, and probability and statistics. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.

Paper

Level

Question 1

SLPaper 1

Given the derivative of a function is $h'(x)=e^x-2$ , determine the intervals where the original function $h(x)$ is increasing or decreasing.

[3]

Question 2

SLPaper 1

Daniela is planning to create a rectangular vegetable garden and wants to maximize her earnings from the produce. She has a fence of 200 meters to enclose the garden, with the length of the garden denoted by $x$ meters.

Daniela sells her produce for 2 USD per square meter, so maximizing the garden's area will maximize her revenue.

Express the area of the garden in terms of $x$ .

[1]

Determine the value of $x$ that maximizes the area of the garden.

[2]

Prove that, with the maximum area, Daniela earns exactly 5000 USD from selling her produce.

[2]

Question 3

HLPaper 1

Given the function $g(x)=e^{2x}$ :

Find the derivative $g(x)$ from first principles.

[5]

Determine the intervals where $g(x)$ is increasing or decreasing.

[3]

Question 4

SLPaper 1

The function $f(x)=\ln(x^2 +1)$ models the growth of a signal's strength over a range of distances $x$ from a source. The signal strength grows differently depending on the direction from the source, and determining intervals of increase or decrease helps engineers position receivers to capture optimal signal quality.

Find the rate of change in signal strength with respect to distance $x$ from the source.

[3]

Determine the intervals on which the receivers would capture a stronger signal.

[4]

Question 5

SLPaper 1

Given the derivative of a function is $f'(x)=2x^2-8x+6$ , determine the intervals where the original function $f(x)$ is increasing or decreasing.

[3]

Question 6

SLPaper 1

Consider the function $f(x)=(x-1)^{2}(3-x)+2$ . The graph of $y=f(x)$ is shown below.

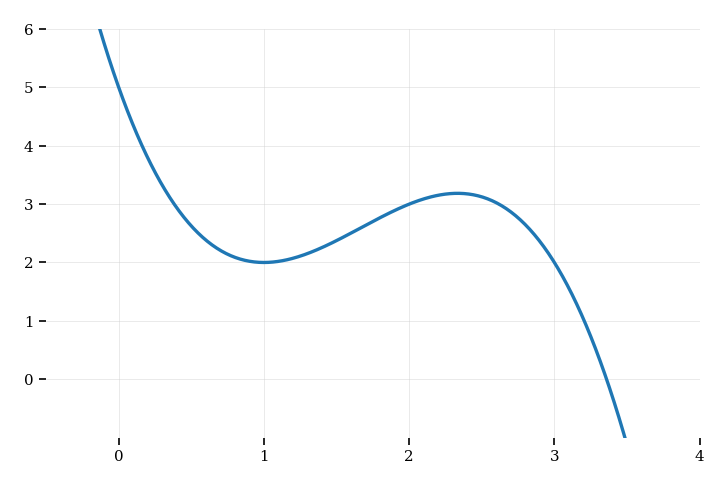
Write down the $y$ -intercept of the graph.

[1]

Expand the expression for $f(x)$ .

[2]

Find $f^{\prime}(x)$ .

[3]

Find the $x$ -coordinates of the points where the tangent is horizontal.

[3]

Determine the intervals where the graph of $y=f(x)$ is increasing.

[2]

Find the range of $f(x)$ for $x \in[0,3]$ .

[3]

Question 7

SLPaper 2

Consider the function $f(x)=x^{3}-3 x^{2}-9 x+7$ . The graph of $y=f(x)$ is shown below.

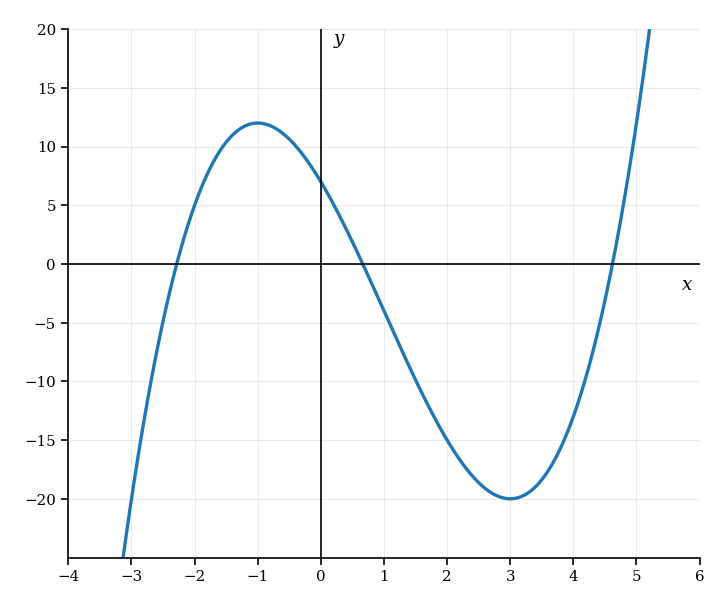
Write down the $y$ -intercept of the graph.

[1]

Find $f^{\prime}(x)$ .

[2]

Find the $x$ -coordinates of the points where the tangent is horizontal.

[3]

Determine the intervals where the graph of $y=f(x)$ is decreasing.

[2]

Find the coordinates of the local minimum point.

[3]

Find the value of $k$ such that $f(x)=k$ has exactly two solutions in $[-2,4]$ .

[3]

Question 8

SLPaper 2

Consider the function $f(x)=-x^{3}+3 x^{2}+9 x-2$ . The graph of $y=f(x)$ is shown below.

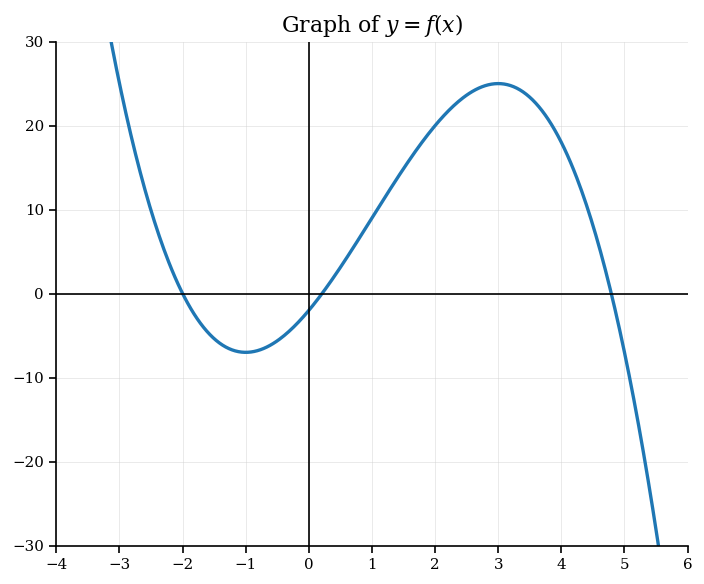
Write down the $y$ -intercept of the graph.

[1]

Find $f^{\prime}(x)$ .

[2]

Find the $x$ -coordinates of the points where the tangent is horizontal.

[3]

Determine the intervals where the graph of $y=f(x)$ is decreasing.

[2]

Find the coordinates of the local maximum point.

[3]

Find the number of solutions to $f(x)=0$ in the interval $[-2,4]$ .

[2]

Question 9

SLPaper 2

Consider the function $f(x)=2 x^{3}-9 x^{2}+12 x-3$ . The graph of $y=f(x)$ is shown below.

Write down the $y$ -intercept of the graph.

[1]

Find $f^{\prime}(x)$ .

[2]

Find the $x$ -coordinates of the points where the tangent to the graph is horizontal.

[3]

Determine the intervals where the graph of $y=f(x)$ is decreasing.

[2]

Find the value of $f(1)$ and state whether this point is a local maximum or minimum.

[3]

Question 10

SLPaper 1

Consider the function $f(x)=x^{3}-6 x^{2}+12 x-4$ . The graph of $y=f(x)$ is shown below.

Write down the $y$ -intercept of the graph.

[1]

Find $f^{\prime}(x)$ .

[2]

Show that the point at $x=2$ is a stationary point and determine its nature.

[3]

Determine the intervals where the graph of $y=f(x)$ is increasing.

[2]

Find the range of $f(x)$ for $x \in[0,4]$ .

[3]

Find the value of $k$ such that $f(x)=k$ has exactly two solutions in $[0,4]$ .

[3]

SL 5.2—Increasing and decreasing functions Questionbank