AHL 5.14—Implicit functions, related rates, optimisation Questionbank

Practice AHL 5.14—Implicit functions, related rates, optimisation with authentic IB Mathematics Analysis and Approaches (AA) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like functions and equations, calculus, complex numbers, sequences and series, and probability and statistics. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.

Paper

Level

Question 1

HLPaper 1

A simple racetrack can be modelled by the equation $y^4+xy^3+x^2y^2+x^3y+x^4=yx$ . This can be seen on the graph below.

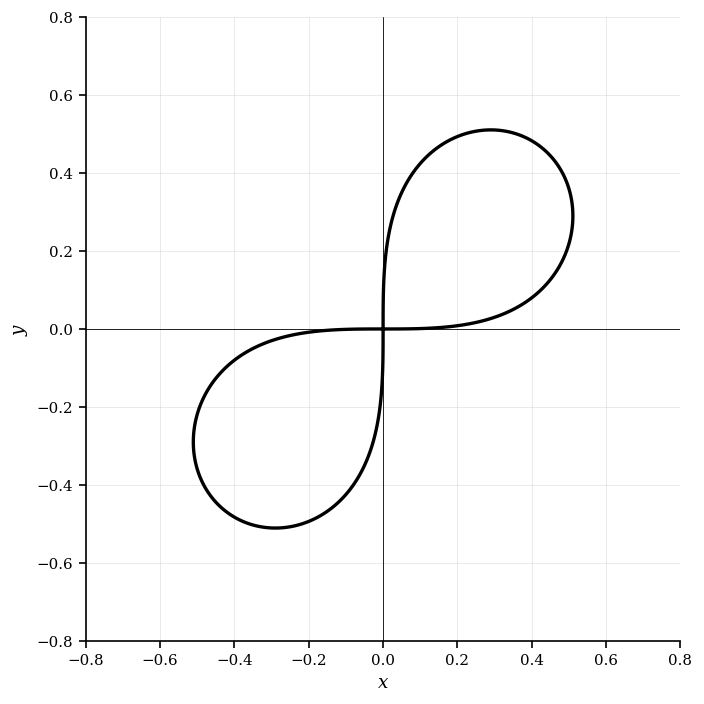
Find an expression for $\frac{dy}{dx}$ .

[4]

Find the limit of $\frac{dy}{dx}$ as $x \to 0$ , given that $y=x$ .

[2]

Question 2

HLPaper 1

Consider a water tank in the shape of an inverted cone with a height of 10 metres and a base radius of 5 metres. Water is being pumped into the tank at a rate of 3 cubic metres per minute.

Find the rate at which the water level is rising when the water is 4 metres deep.

[5]

Question 3

HLPaper 2

A rectangular piece of cardboard with dimensions $24$ cm by $36$ cm is to be made into an open box by cutting squares of side length $x$ cm from each corner and folding up the sides.

Find the volume $V$ of the box in terms of $x$ .

[2]

Determine the value of $x$ that maximizes the volume of the box.

[3]

Verify that the value of $x$ found in part 2 is a maximum by using the second derivative test.

[2]

Calculate the maximum volume of the box. Give your answer correct to two decimal places.

[2]

Question 4

HLPaper 1

A water tank is shaped like an inverted right circular cone with a semi-vertical angle of $30^\circ$ . The height of the cone is $10 \, \text{m}$ . Water is being pumped into the tank at a constant rate of $0.5 \, \text{m}^3 \, \text{min}^{-1}$ . Let $h$ be the depth of the water in the tank and $r$ be the radius of the water surface at time $t$ minutes.

Show that the volume of water $V$ in the tank is given by $V = \dfrac{\pi h^3}{9}$ .

[2]

Find the rate at which the water level is rising when the depth of the water is $4 \, \text{m}$ .

[4]

At the instant when the water level is $4 \, \text{m}$ , the water supply is turned off and water begins to leak out of the bottom at a rate proportional to the square root of the depth of the water. Given that the water level is initially decreasing at a rate of $0.01 \, \text{m} \, \text{min}^{-1}$ at this instant, find the differential equation satisfied by $h$ .

[3]

Question 5

HLPaper 1

Consider the curve defined by the equation $x^2 - xy + y^2 = 12.$

Find an expression for $\frac{dy}{dx}$ in terms of $x$ and $y$ .

[4]

Find the coordinates of the two points on the curve where the tangent is horizontal.

[4]

Determine the nature of the stationary points found in part 2.

[4]

Question 6

HLPaper 1

Determine the coordinates of the locations on the curve $y^3 + 3xy^2 - x^3 = 27$ where $\frac{dy}{dx} = 0$ .

[9]

Question 7

HLPaper 2

A small marble is free to move along a smooth wire in the shape of the curve $y=\frac{10}{3-2e^{-0.5x}}, \quad x \geq 0$

At the point on the curve where $x=4$ , it is given that $\frac{dy}{dt}=-0.1\,\mathrm{m\,s^{-1}}$ .

Find the value of $\frac{dx}{dt}$ at this instant.

[3]

Find an expression for $\frac{dy}{dx}$ .

[3]

Question 8

HLPaper 2

Consider the differential equation $z^2 \frac{\mathrm{d}w}{\mathrm{d}z} = w^2 - 2z^2$ for $z > 0$ and $w > 2z$ .

It is given that $w = 3$ when $z = 1$ .

Use Euler's technique, with a step length of 0.1, to find an approximate value of $w$ when $z = 1.5$ .

[4]

Use the substitution $w = vz$ to show that $z \frac{\mathrm{d}v}{\mathrm{d}z} = v^2 - v - 2$ .

[3]

By solving the differential equation, show that $w = \frac{8z + z^4}{4 - z^3}$ .

[8]

Find the actual value of $w$ when $z = 1.5$ .

[1]

Using the graph of $w = \frac{8z + z^4}{4 - z^3}$ , suggest a reason why the approximation given by Euler's technique in part 1 is not a good estimate to the actual value of $w$ at $z = 1.5$ .

[1]

Question 9

HLPaper 2

A particle $P$ moves along a straight line such that its velocity, $v$ m s $^{-1}$ , at time $t$ seconds is given by $v(t) = e^{\sin t} - 2\sin(3t), \quad 0 \le t \le 5.$

Find the initial acceleration of the particle.

[4]

Find the times $t \in [0, 5]$ when the particle is at rest.

[2]

Find the total distance travelled by the particle in the first 4 seconds.

[3]

Given that the particle starts at the origin at $t=0$ , determine the displacement of the particle from the origin at $t=5$ .

[2]

Question 10

HLPaper 2

Consider the curve $D$ given by $y=x-xy\,\ln(xy)$ where $x>0, y>0$ .

Show that $\frac{dy}{dx} + \left(x\frac{dy}{dx} + y\right) (1 + \ln(xy)) = 1$

[3]

Hence find the equation of the tangent to $D$ at the point where $x=1$ .

[5]