RevisionDojo

SL 5.5—Integration introduction, areas between curve and x axis - IB Questionbank | RevisionDojo

Practice SL 5.5—Integration introduction, areas between curve and x axis with authentic IB Mathematics Analysis and Approaches (AA) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like functions and equations, calculus, complex numbers, sequences and series, and probability and statistics. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.

Paper

Level

Question 1

HLPaper 1

Consider the functions $f(x) = x^3$ and $g(x) = x^2$ over the interval $[0, 1]$ .

Find the area between the curves $f(x) = x^3$ and $g(x) = x^2$ from $x = 0$ to $x = 1$ .

[2]

Question 2

SL & HLPaper 1

Consider the function $g(x)=\frac{\sin(2x)}{2}(\frac{1}{\tan(x)}+2)-\sin^2(x)$

Show that $g(x)=\sin(2x)+\cos(2x)$

[5]

Show that $g''(x)=-4g(x)$

[3]

Hence, using your answer from part (b), find $\int\!g(x)\,dx$ in terms of $g(x)$

[4]

Question 3

HLPaper 1

Evaluate: $\int_0^{\pi} \cos(\pi - x) \, dx.$

[3]

Question 4

SLPaper 1

Consider the function $g(x) = x^2 - 4x + 3$ .

Calculate the area between the curve and the x-axis from $x = 1$ to $x = 3$ .

[3]

Question 5

SLPaper 2

The graph of $y=f^{\prime}(x), 0 \leq x \leq 4$ , is shown below. The curve intercepts the x -axis at $(1,0)$ and $(3,0)$ and has a local maximum at $(2,2)$ . The area enclosed by the curve and the x -axis between $x=0$ and $x=1$ is 1 . Given $f(0)=2$ ,

Find the x -coordinate of the local minimum on the graph of $y=f(x)$ .

[1]

Find the value of $f(1)$ .

[3]

Find the value of $f(3)$ .

[2]

Question 6

HLPaper 2

Express $\frac{4x^2+5x+3}{(x+1)(x^2+2x+2)}$ in partial fractions.

[6]

Hence, evaluate $\int_0^1 \frac{4x^2+5x+3}{(x+1)(x^2+2x+2)} \, dx$ .

[7]

Question 7

SLPaper 1

Define $g(x)=\sin ^{-1}\left(\frac{x}{3}\right)+\cos ^{-1}\left(\frac{x}{3}\right)$ for $x \in[-3,3]$ , and $h(x)=e^{g(x)}$ .

Show that $g(x)=\frac{\pi}{2}$ for all $x \in[-3,3]$ .

[2]

Find the exact coordinates of the intersection of $h$ and the line $y=2 x+1$ .

[3]

Find the exact coordinates of the point where the tangent to $h$ at $x=1$ intersects the $x$ -axis.

[4]

Sketch the graph of $y=h(x)$ and $y=2 x+1$ , showing the intersection and tangent at $x=1$ .

[3]

Find the exact area of the region bounded by $h, y=2 x+1$ , and the $y$ -axis.

[5]

Question 8

SLPaper 2

Consider the function $f(x)=\ln \left(\frac{x^{2}+1}{x^{2}-4}\right)$ , defined for $x \in \mathbb{R} \backslash\{-2,2\}$ .

Find the equations of all vertical and horizontal asymptotes of the graph of $y=f(x)$ .

[3]

Determine the coordinates of the points where the graph of $f$ intersects the coordinate axes.

[3]

Show that $f$ is an odd function, and hence deduce the symmetry of its graph.

[2]

Sketch the graph of $y=f(x)$ , clearly indicating the asymptotes, intercepts, and the behavior near $x= \pm 2$ .

[4]

The region bounded by the curve $y=f(x)$ , the $x$ -axis, and the lines $x=\sqrt{2}$ and $x=\sqrt{3}$ is rotated through $2 \pi$ about the $y$ -axis. Find the exact volume of the solid generated.

[6]

Question 9

HLPaper 2

Let $f(x) = \frac{2x^3 + x^2 - 11x - 12}{(x-2)(x+1)^2}$ .

Express $f(x)$ in partial fractions.

[6]

Hence, find the exact value of $\int_3^4 f(x) \, dx$ .

[4]

Question 10

SLPaper 1

Find $\int\left(4 x^{2}-3 x+2\right) d x$ .

[3]

Given $f^{\prime}(x)=4 x^{2}-3 x+2$ and $f(2)=5$ , find $f(x)$ .

[3]

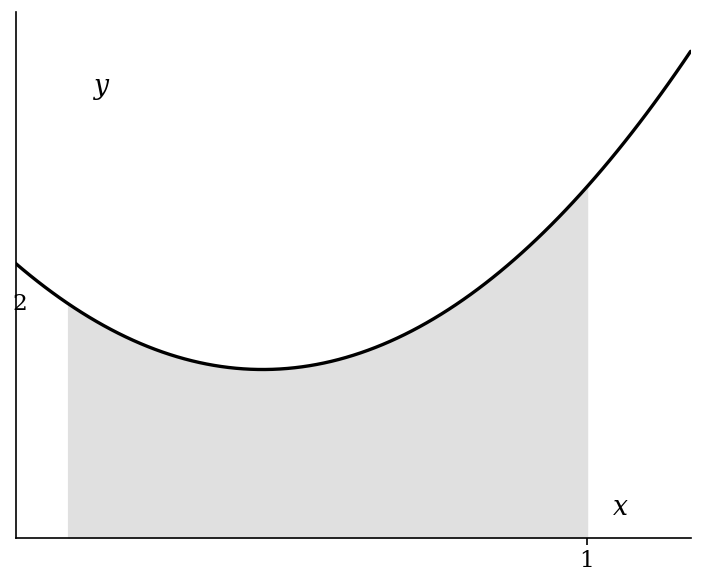
Calculate the area under the curve $y=4 x^{2}-3 x+2$ from $x=0$ to $x=1$ .

[4]

SL 5.5—Integration introduction, areas between curve and x axis Questionbank