RevisionDojo

SL 5.11—Definite integrals, areas under curve onto x-axis and areas between curves - IB Questionbank | RevisionDojo

Practice SL 5.11—Definite integrals, areas under curve onto x-axis and areas between curves with authentic IB Mathematics Analysis and Approaches (AA) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like functions and equations, calculus, complex numbers, sequences and series, and probability and statistics. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.

Paper

Level

Question 1

HLPaper 1

By using the substitution $u=\sec x$ or otherwise, find an expression for $\int_0^{\frac{\pi}{3}} \sec^n x \tan x, dx$ in terms of $n$ , where $n$ is a non-zero real number.

[6]

Question 2

HLPaper 1

Consider the functions $f(x) = x^3$ and $g(x) = x^2$ over the interval $[0, 1]$ .

Find the area between the curves $f(x) = x^3$ and $g(x) = x^2$ from $x = 0$ to $x = 1$ .

[2]

Question 3

SL & HLPaper 1

Consider the quadratic function $f(x) = 2(x - 2)^2 + 4$ .

Describe the transformations applied to the function $y = x^2$ to obtain the function $f(x)$ .

[3]

Given that $x^2\geq f(x)$ under the interval $[2,4]$ , find the area between the curves $y = x^2$ and $f(x) = 2(x - 2)^2 + 4$ within that interval.

[5]

Question 4

HLPaper 1

Consider a water tank in the shape of an inverted cone with a height of 10 meters and a base radius of 5 meters. Water is being pumped into the tank at a rate of 3 cubic meters per minute.

Find the rate at which the water level is rising when the water is 4 meters deep.

[5]

Question 5

SL & HLPaper 1

Consider the quadratic function $f(x) = -2(x+1)^2+5$ .

The function $g(x) = x^2$ is transformed to the function $f(x) = -2(x + 1)^2 + 5$ . Describe the transformations applied to $g(x)$ to obtain $f(x)$ .

[4]

Find the vertex of the function $f(x) = -2(x + 1)^2 + 5$ and explain why it is a maximum.

[3]

Find the area between the curve $f(x)$ and $g(x)=x^2$ within the interval $[-1,0]$

[4]

Question 6

HLPaper 1

Use the substitution $v = y^{\frac{1}{2}}$ to find

$\int \frac{dy}{y^{\frac{3}{2}} + y^{\frac{1}{2}}}$ .

[4]

Hence find the value of $\frac{1}{2}\int\limits_1^9 {\frac{{dy}}{{y^{\frac{3}{2}}} + {y^{\frac{1}{2}}}}}$ , expressing your answer in the form arctan $r$ , where $r \in \mathbb{Q}$ .

[3]

Question 7

HLPaper 1

Let $f(x)=4-x^2$ , where $x \geq 0$ . The shaded region is enclosed by the graph of $f$ , the $x$ -axis, and the $y$ -axis.

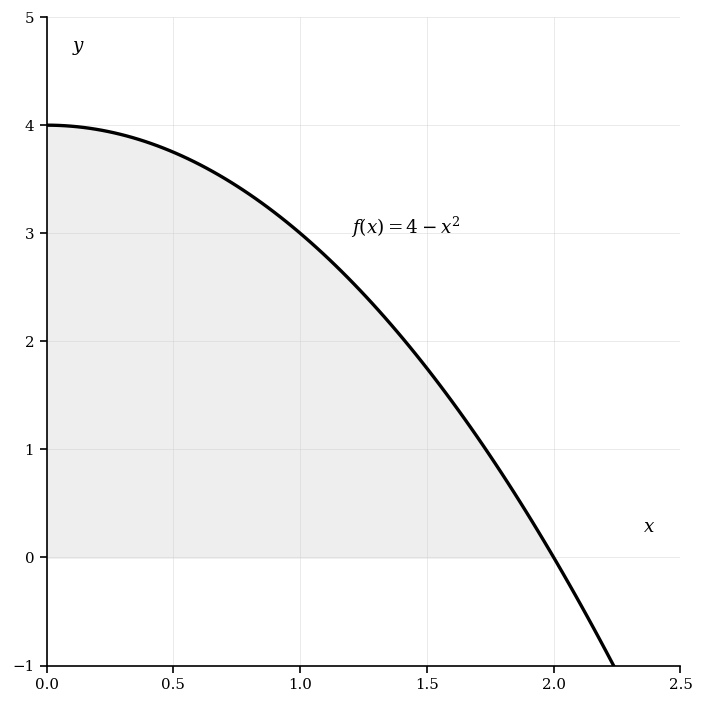
Find the $x$ -coordinate of the point where the graph of $f(x)$ intersects the $x$ -axis

[2]

Find the area of the shaded region.

[2]

Find the volume of the solid formed when the shaded region is revolved $360^{\circ}$ about the $x$ axis.

[4]

Question 8

SLPaper 1

Consider the function $f(x)=\frac{x \ln x}{x^{2}-1}$ defined for $x>1$ .

Express $f(x)$ as a sum of partial fractions.

[4]

Show that $\int \frac{x \ln x}{x^{2}-1} d x=\frac{1}{2} \ln x \ln \left(\frac{x+1}{x-1}\right)+\frac{1}{4} \ln ^{2}(x+1)-\frac{1}{4} \ln ^{2}(x-1)+c$ .

[5]

Find the exact area of the region enclosed by the graph of $y=f(x)$ , the x -axis, and the lines $x=2$ and $x=e$ .

[5]

Question 9

HLPaper 2

Express $\frac{4x^2+5x+3}{(x+1)(x^2+2x+2)}$ in partial fractions.

[6]

Hence, evaluate $\int_0^1 \frac{4x^2+5x+3}{(x+1)(x^2+2x+2)} \, dx$ .

[7]

Question 10

SLPaper 1

The function $f(x)=x \sin x$ is defined for $0 \leq x \leq 2 \pi$ .

Show that $\int x \sin x d x=\sin x -x \cos x+c$ .

[4]

Find the area enclosed by the curve $y=f(x)$ and the x-axis from $x=0$ to $x=2 \pi$ .

[4]

SL 5.11—Definite integrals, areas under curve onto x-axis and areas between curves Questionbank