RevisionDojo

SL 5.1—Introduction of differential calculus - IB Questionbank | RevisionDojo

Practice SL 5.1—Introduction of differential calculus with authentic IB Mathematics Analysis and Approaches (AA) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like functions and equations, calculus, complex numbers, sequences and series, and probability and statistics. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.

Paper

Level

Question 1

HLPaper 1

This question involves the introduction of differential calculus and focuses on finding the derivative of a function using first principles and applying basic differentiation rules.

Consider the function $f(x) = 3x^2 - 2x + 4$ . Using the definition of the derivative, find $f'(x)$ .

[5]

Using the result from part 1, find the slope of the tangent to the curve $y = f(x)$ at the point where $x = 1$ .

[2]

Find the equation of the tangent line to the curve $y = f(x)$ at the point where $x = 1$ .

[3]

Determine the x-coordinates where the tangent to the curve $y = f(x)$ is horizontal.

[2]

Question 2

HLPaper 1

Given the function $g(x)=e^{2x}$ :

Find the derivative $g(x)$ from first principles.

[5]

Determine the intervals where $g(x)$ is increasing or decreasing.

[3]

Question 3

SLPaper 1

This question involves understanding the basics of differential calculus and applying the concept of derivatives to solve problems.

Consider the function $f(x) = x^3 - 3x^2 + 2x + 5$ .

Find the derivative of the function $f(x)$ with respect to $x$ .

[2]

Determine the critical points of the function $f(x)$ .

[3]

Determine whether each critical point is a local maximum, local minimum, or neither.

[3]

Sketch the graph of the function $f(x) = x^3 - 3x^2 + 2x + 5$ , indicating the critical points and their nature.

[3]

Question 4

SLPaper 1

An engineer is examining the shape of a parabolic reflector modeled by the function ${g(x)=4x^2−2x}$ , where x represents the distance from the reflector's center, and g(x) gives the height of the reflector at each point. The engineer needs to understand the slope of the reflector surface at specific points to optimize the angle at which it reflects light.

Find the expression for $g'(x)$ to determine the slope of the reflector surface at any point $x$ .

[2]

Calculate the slope of the reflector at $x=1$ to understand its angle at that position.

[2]

Write the equation of the tangent line to the reflector’s curve at $x=1$ , which represents the line tangent to the reflector at this point.

[3]

Question 5

SLPaper 2

The function $g(t)=e^{-0.5t}$ models how the temperature of a hot drink cools over time $t$ , measured in minutes, as it sits out in a room. The function describes the temperature decrease, with $g(t)$ representing the temperature of the drink at any given time $t$ .

Determine how quickly the temperature of the drink is decreasing at any time t by finding the expression for the rate of change $g'(t)$ .

[3]

Explain what the rate of change tells us about the cooling process of the drink over time.

[2]

Calculate the rate of temperature change specifically at t=2 minutes, and interpret what this value on how quickly the drink is cooling at that time.

[3]

Question 6

SLPaper 2

The function $f(x)=\frac{3x+1}{x^2-4}$ models the stress on a structural beam as a function of position $x$ along the beam. However, the stress becomes infinitely large near certain points, creating critical regions for analysis.

Identify any vertical and horizontal asymptotes of $f(x)=\frac{3x+1}{x^2-4}$ , which represent points where stress approaches infinity and the overall behavior of stress along the beam.

[3]

Describe the behavior of the stress $f(x)$ as $x \to \infty$ and $x \to -\infty$ , and interpret its significance.

[2]

Sketch the graph of $f(x)$ , marking key points and asymptotes, to illustrate the beam's stress distribution.

[3]

Question 7

HLPaper 1

Given the function $f(x)=x^2+3x$ :

Find the derivative of $f(x)$ from first principles.

[5]

Determine the intervals where $f(x)$ is increasing or decreasing.

[3]

Question 8

SLPaper 1

This question assesses understanding of the introduction to differential calculus, specifically involving the concept of the derivative and its application.

Given the function $f(x) = 3x^3 - 5x^2 + 2x - 4$ , find the derivative $f'(x)$ .

[2]

Determine the equation of the tangent line to the curve $y = f(x)$ at the point where $x = 1$ .

[3]

Find the second derivative $f''(x)$ of the function $f(x) = 3x^3 - 5x^2 + 2x - 4$ .

[2]

Determine the concavity of the function $f(x) = 3x^3 - 5x^2 + 2x - 4$ at the point where $x = 1$ .

[1]

Find the critical points of the function $f(x) = 3x^3 - 5x^2 + 2x - 4$ .

[2]

Question 9

SLPaper 1

The diagram shows the graph of the function $f(x) = x^3 - 3x^2 - 9x + 27$ and its tangent at point P(3, 0).

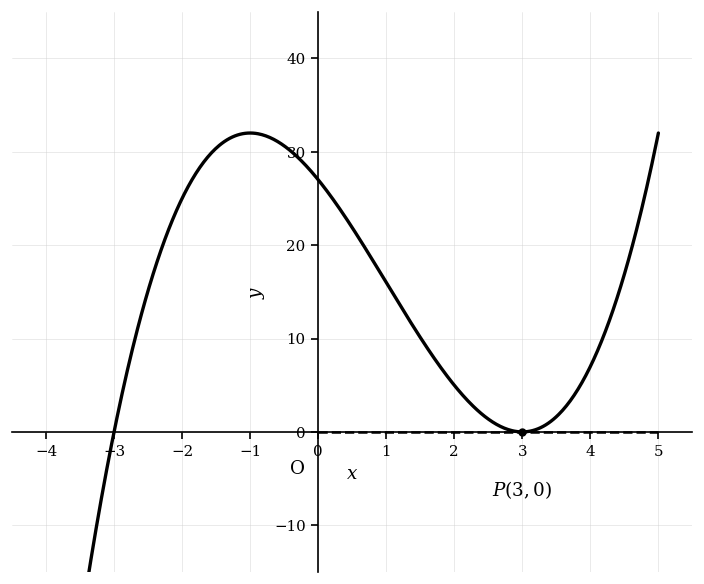
Find the derivative of the function $f(x) = x^3 - 3x^2 - 9x + 27$ .

[1]

Determine the slope of the tangent to the graph of $f(x)$ at point P(3, 0).

[1]

Find the equation of the tangent line to the graph of $f(x)$ at point P(3, 0).

[1]

Find the coordinates of the points where the tangent to the graph of $f(x)$ is parallel to the tangent at point P(3, 0).

[2]

Verify that the tangent line at point $(-1, 32)$ is indeed horizontal.

[1]

Question 10

SLPaper 1

The function $f(x)=x^3-2x+1$ is given.

Calculate $f'(2)$ .

[2]

Interpret the meaning of the derivative value found in part (1).

[2]

Describe what this derivative value tells us about the behavior of the function at $x=2$ .

[2]

SL 5.1—Introduction of differential calculus Questionbank