RevisionDojo

SL 3.5—Unit circle definitions of sin, cos, tan. Exact trig ratios, ambiguous case of sine rule - IB Questionbank | RevisionDojo

Practice SL 3.5—Unit circle definitions of sin, cos, tan. Exact trig ratios, ambiguous case of sine rule with authentic IB Mathematics Analysis and Approaches (AA) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like functions and equations, calculus, complex numbers, sequences and series, and probability and statistics. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.

Paper

Level

Question 1

SLPaper 1

Consider the function $f(x) = 3 \sin\left(kx + \frac{\pi}{4}\right) - 1$ .

Find the amplitude of $f(x)$ .

[1]

Determine the possible values of $k$ such that $f(x)$ has a period of $12\pi$ .

[3]

Given that $k > 0$ , find the $x$ -coordinates of the maximum and minimum points of $f(x)$ in the domain $0 \le x \le 2\pi$ .

[6]

Question 2

SLPaper 1

Let $g(x) = \sin(x) + \cos(x)$ .

Find the derivative of the function $g(x)$ .

[1]

Find the equation of the tangent line to the graph of $g(x)$ at $x = \frac{\pi}{4}$ .

[3]

Hence, or otherwise, show that at $x=\frac{\pi}{4}$ the function attains its maximum.

[4]

Question 3

SLPaper 1

The first two terms of an infinite geometric sequence are $v_1 = 18$ and $v_2 = 12\sin^{2} \alpha$ , where $0 < \alpha < 2\pi$ , and $\alpha \neq \pi$ .

Find an expression for $r$ in terms of $\alpha$ .

[2]

Find the values of $\alpha$ which give the greatest value of the sum.

[6]

Question 4

SL & HLPaper 1

Consider a geometric sequence where the first term $a_1 = 4\sin x$ and the second term $a_2 = \sin 4x$ , where $\sin x \neq 0$ .

Find the common ratio $r$ of this geometric sequence in terms of $\cos x$ and $\cos 2x$ .

[4]

Given that $|r| \neq 1$ , explain why the sum to infinity exists and find it for $x=\frac{\pi}{6}$ , giving your answer in the form $\frac{a+b\sqrt{c}}{d}$ .

[5]

Question 5

SLPaper 1

Prove the identity
$\frac{1-\tan^2\theta}{1+\tan^2\theta}=\cos(2\theta),$ for all values of $\theta$ for which both sides are defined.

Start from the left-hand side and express everything in terms of $\sin\theta$ and $\cos\theta$ .

[3]

Hence, or otherwise, show that $\sin(2\theta)=\frac{2\tan\theta}{1+\tan^2\theta}.$

[3]

If $\tan\theta=\dfrac{3}{4}$ , find the exact values of $\sin(2\theta)$ and $\cos(2\theta)$ .

[4]

Question 6

SLPaper 1

Let $\sin 20^{\circ}=p$ and $\cos 20^{\circ}=q$ (so that $p^{2}+q^{2}=1$ ). By observing the unit circle, express the following in terms of $p$ and/or $q$ .

$\sin 340^{\circ}$

[1]

$\cos 340^{\circ}$

[1]

$\tan 340^{\circ}$

[1]

$\sin \left(-20^{\circ}\right)$

[1]

$\cos \left(-20^{\circ}\right)$

[1]

$\tan \left(-20^{\circ}\right)$

[1]

Question 7

SLPaper 1

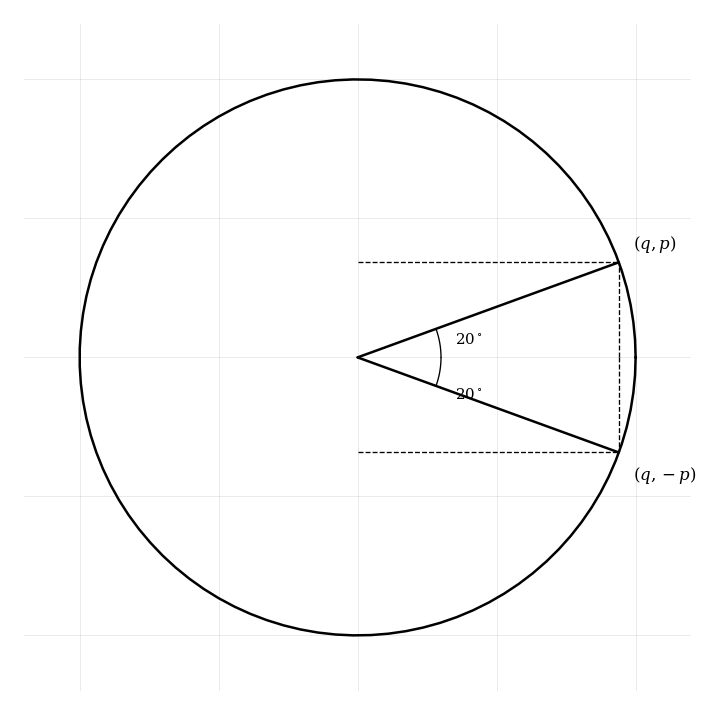
A point $P$ moves around the unit circle centered at the origin $O(0,0)$ with coordinates $P(\cos\theta,\sin\theta)$ .

At a certain instant, the $x$ -coordinate of $P$ is $-\dfrac{\sqrt{3}}{2}$ .

Find all possible values of $\sin\theta$ .

[2]

If $P$ lies in the third quadrant, find the exact values of $\sin(2\theta)$ , $\cos(2\theta)$ , and $\tan(2\theta)$ .

[4]

Verify that the identity $1+\tan^2(2\theta)=\sec^2(2\theta)$ holds for your values.

[2]

A quantity $Q$ measured at $P$ is defined by $Q = (\cos\theta-\sin\theta)^2$ . Determine the maximum and minimum possible values of $Q$ , giving exact values.

[3]

Hence find the range of $\theta$ (in radians, $0\le\theta<2\pi$ ) for which the quantity $Q$ is greater than $1$ .

[3]

Question 8

SLPaper 1

A point $P$ moves around the unit circle centered at the origin $O(0,0)$ with coordinates $P(\cos\theta, \sin\theta)$ .

At a certain instant, the $y$ -coordinate of $P$ is $-\frac{4}{5}$ .

Find all possible values of $\cos\theta$ .

[2]

If $P$ lies in the fourth quadrant, find the exact values of $\sin(2\theta)$ , $\cos(2\theta)$ , and $\tan(2\theta)$ .

[4]

Verify that the identity $\cot^2(2\theta) + 1 = \csc^2(2\theta)$ holds for your values.

[2]

A rotating light beam at $P$ has intensity $I$ given by the equation $I = (\sqrt{5}\sin\theta + \sqrt{5}\cos\theta)^2$ .

Determine the maximum and minimum possible intensities, giving exact values.

[3]

Hence find the range of $\theta$ (in radians, $0 \le \theta < 2\pi$ ) for which the intensity is less than $5$ .

[3]

Question 9

SLPaper 1

A point $P$ moves around the unit circle centered at the origin $O(0,0)$ with coordinates $P(\cos\theta, \sin\theta)$ .

At a certain instant, the $x$ -coordinate of $P$ is $\dfrac{2}{\sqrt{13}}$ .

Find all possible values of $\sin\theta$ .

[2]

If $P$ lies in the first quadrant, find the exact values of $\sin(2\theta)$ , $\cos(2\theta)$ , and $\tan(2\theta)$ .

[4]

Verify that the identity $1+\cot^2(2\theta)=\csc^2(2\theta)$ holds for your values.

[2]

A quantity $Q$ defined at a general point $P$ on the circle is given by $Q = (\sin\theta + \cos\theta)^2$ .

Determine the maximum and minimum possible values of $Q$ , giving exact values.

[3]

Hence find the range of $\theta$ (in radians, $0 \le \theta < 2\pi$ ) for which the quantity $Q$ is greater than $0$ .

[3]

Question 10

SLPaper 1

A point $P$ moves around the unit circle centered at the origin $O(0,0)$ with coordinates $P(\cos\theta,\sin\theta)$ .

At a certain instant, the $x$ -coordinate of $P$ is $\frac{3}{5}$ .

Find all possible values of $\sin\theta$ .

[2]

If $P$ lies in the fourth quadrant, find the exact values of $\sin(2\theta)$ , $\cos(2\theta)$ , and $\tan(2\theta)$ .

[4]

Verify that the identity $1+\tan^2(2\theta)=\sec^2(2\theta)$ holds for your values.

[2]

A rotating beacon at the point $P$ emits a light beam of intensity $I$ given by $I = (\sin\theta+\cos\theta)^2$ . As $\theta$ increases from $0$ to $2\pi$ , determine the maximum and minimum possible intensities, giving exact values.

[4]

Hence find the range of $\theta$ (in radians, $0\le\theta<2\pi$ ) for which the intensity exceeds 1.5.

[3]

SL 3.5—Unit circle definitions of sin, cos, tan. Exact trig ratios, ambiguous case of sine rule Questionbank