Unit Circle Definitions and Exact Trigonometric Ratios
The Unit Circle
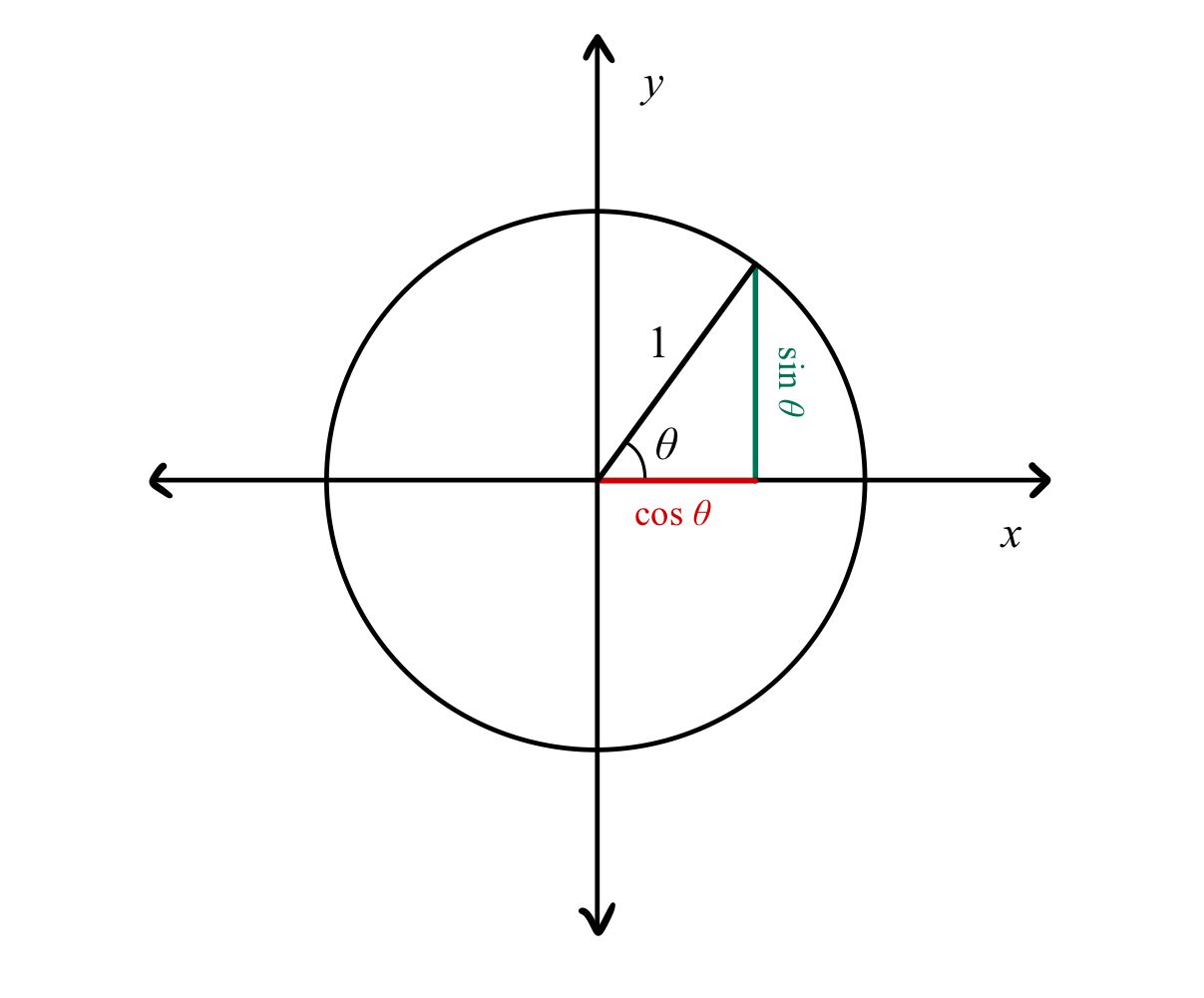
The unit circle is a circle with radius 1 centered at the origin (0,0).
On the unit circle:
- The x-coordinate is $\cos \theta$
- The y-coordinate is $\sin \theta$
- The slope of the radius line is $\tan \theta = \frac{\sin \theta}{\cos \theta}$
Remember that any point on the unit circle can be written as $(\cos \theta, \sin \theta)$ because the radius is always 1!
Exact Trigonometric Ratios
Here are the exact values you need to know:
For angle θ:
| $\theta$ (degrees) | $\theta$ (radians) | $\sin\theta$ | $\cos\theta$ | $\tan\theta$ |
|---|---|---|---|---|
| $0°$ | $0$ | $0$ | $1$ | $0$ |
| $30°$ | $\frac\pi6$ | $\frac12$ | $\frac{\sqrt3}2$ | $\frac{\sqrt3}3$ |
| $45°$ | $\frac\pi4$ | $\frac{\sqrt2}2$ | $\frac{\sqrt2}2$ | $1$ |
| $60°$ | $\frac\pi3$ | $\frac{\sqrt3}2$ | $\frac12$ | $\sqrt3$ |
| $90°$ | $\frac\pi2$ | $1$ | $0$ | undefined |
These values come from special right triangles (30-60-90 and 45-45-90) inscribed in the unit circle.
Unit Circle and Ratios
Depending on which quadrant $\theta$ is in, the values of $\sin \theta, \cos \theta, \tan \theta $ may change sign.
- Since $\sin\theta$ is correlated with the $y$-value of the point on the unit circle, $\sin\theta$ is positive in the first and second quadrants ($y>0$), and negative in the third and fourth ($y<0$).