- IB
- AHL 3.9—Reciprocal trig ratios and their pythagorean identities. Inverse circular functions
Practice AHL 3.9—Reciprocal trig ratios and their pythagorean identities. Inverse circular functions with authentic IB Mathematics Analysis and Approaches (AA) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like functions and equations, calculus, complex numbers, sequences and series, and probability and statistics. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
Prove that: for
Evaluate: .
Prove that and hence show that
Prove that and hence show that
Solve, for , the equation . (You may use .) Give your answer to 3 significant figures.
Let . Find the values of and . Give your answers to 3 significant figures. State the quadrant of and verify that .
A line through the origin has equation and makes an angle with the positive -axis, so that . Find all such that , and the corresponding slopes (to 3 significant figures).
Prove that and hence show that
Prove and hence show that
Solve, for , the equation .
Give your answer to 3 significant figures.
Let . Find exact decimal values of and .
State the quadrant of and verify that .
A line through the origin has slope .
Find all such that , and the corresponding slopes (3 s.f.).
Prove that
Show that .
Find the coordinates of the local maximum and local minimum points on the graph of , for .
Find the solution of the equation , for .
This question involves trigonometric identities, equations, and properties.
Prove that and hence show that
Solve, for , the equation .
(You may use . )
Give your answer to 3 significant figures.
Let . Find the values of and .
State the quadrant of and verify that .
A line through the origin has equation and makes an angle with the positive -axis, so that .
Find all such that , and the corresponding slopes (to 3 significant figures).
It is given that where . Use the following triangle:
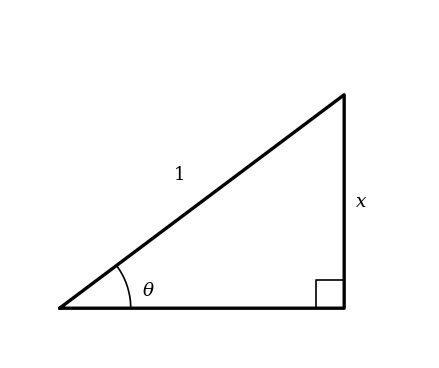
Find .
Consider the function
Sketch the graph of , in the interval and state the -intercepts, the equations of the asymptotes, and the coordinates of the maximum and minimum points.
Show that roots of the equation satisfy the equation
Show that
Sketch the graph of , in the interval [4]
Sketch the graph of , in the interval
On the same diagram sketch the graph of , in the interval , indicating clearly the equations of any asymptotes.
Use your sketch to solve:
(i) the equation in the interval
(ii) the inequality in the interval