AHL 3.12—Vector definitions Questionbank

Practice AHL 3.12—Vector definitions with authentic IB Mathematics Analysis and Approaches (AA) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like functions and equations, calculus, complex numbers, sequences and series, and probability and statistics. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.

Paper

Level

Question 1

HLPaper 1

Let $\mathbf{u} = \begin{pmatrix} 1 \\ 0 \\ 2 \end{pmatrix}$ and $\mathbf{v} = \begin{pmatrix} 3 \\ -1 \\ 1 \end{pmatrix}$ . Let $\mathbf{w}$ be a vector that is perpendicular to both $\mathbf{u}$ and $\mathbf{v}$ .

Find a vector $\mathbf{w}$ that is perpendicular to both $\mathbf{u}$ and $\mathbf{v}$ .

[4]

Question 2

HLPaper 1

Consider the plane $\Pi_1$ given by the equation $x + 2y - z = 4$ and the plane $\Pi_2$ given by the equation $3x - y + 4z = 10$ .

Find a vector equation of the line of intersection of the planes $\Pi_1$ and $\Pi_2$ .

[4]

Verify that the line of intersection found is perpendicular to the normal vectors of both planes.

[3]

Question 3

HLPaper 1

In this question, all lengths are in metres and time is in seconds. Consider two particles, $A_1$ and $A_2$ , which start to move at the same time. Particle $A_1$ moves in a straight line such that its displacement from a fixed point is given by $s(t) = 10 - \frac{7}{4}t^2$ , for $t \geq 0$ .

Find an expression for the velocity of $A_1$ at time $t$ .

[2]

Particle $A_2$ also moves in a straight line. The position of $A_2$ is given by $\mathbf{r} = t\begin{pmatrix} 4 \\ -3 \end{pmatrix}$ . The speed of $A_1$ is greater than the speed of $A_2$ when $t > q$ . Find the value of $q$ .

[5]

Question 4

HLPaper 2

In 3D space, the points are
$A(3,1,-1),\quad B(7,4,0),\quad C(5,-2,6).$

Find the vectors $\overrightarrow{AB}$ and $\overrightarrow{AC}$ .

[3]

Compute $\overrightarrow{AB}\cdot\overrightarrow{AC}$ and hence find $\angle BAC$ to 3 s.f.

[4]

Find the unit vector in the direction of $\overrightarrow{AB}+\overrightarrow{AC}$ .

[3]

Find the perpendicular distance from $A$ to the line $BC$ .

[3]

Question 5

HLPaper 1

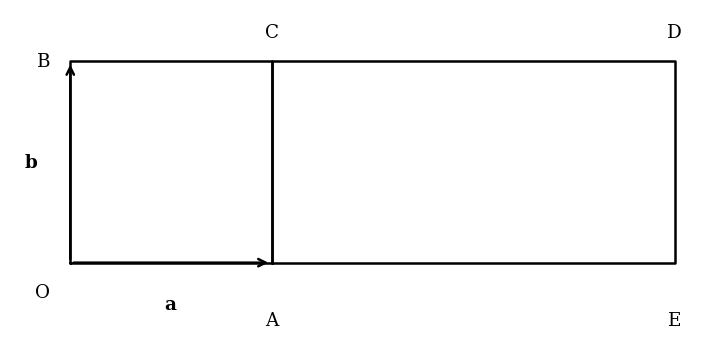
In the following diagram $OBCA$ is a square of side 5 cm while $ACDE$ is a rectangle of length 10 cm and width 5 cm. Let $\mathbf{a}=\overrightarrow{OA}$ and $\mathbf{b}=\overrightarrow{OB}$ .

Express the following vectors in terms of $\mathbf{a}$ and $\mathbf{b}$

$\overrightarrow{OC}$

[1]

$\overrightarrow{OD}$

[1]

$\overrightarrow{AD}$

[1]

$\overrightarrow{BA}$

[1]

Question 6

HLPaper 1

Let $\mathbf{a}=\begin{pmatrix}2 \\ 1 \\ 2\end{pmatrix}$ and $\mathbf{b}=\begin{pmatrix}1 \\ 1 \\ 1\end{pmatrix}$ .

Find the magnitude of $\mathbf{a}$ .

[2]

Find the magnitude of $\mathbf{b}$ .

[2]

Find the unit vector in the direction of $\mathbf{a}$ .

[2]

Find the unit vector in the direction of $\mathbf{b}$ .

[2]

Question 7

HLPaper 1

Consider two vectors $\vec{a} = \begin{pmatrix} 2 \\ -1 \\ 3 \end{pmatrix}$ and $\vec{b} = \begin{pmatrix} 4 \\ 2 \\ -1 \end{pmatrix}$

Calculate $\vec{a} \times \vec{b}$

[3]

Question 8

HLPaper 2

A construction company is analyzing the forces acting on a beam supported by two cables. The forces exerted by the cables are represented by vectors. Forces are measured in Newtons (N). The company needs to ensure that the angle between the two force vectors is within a safe range to prevent structural failure.

Given the force vectors $\mathbf{F_1} = \begin{pmatrix} 3 \\ 4 \\ 0 \end{pmatrix}$ and $\mathbf{F_2} = \begin{pmatrix} 5 \\ 0 \\ 12 \end{pmatrix}$ , calculate the dot product $\mathbf{F_1} \cdot \mathbf{F_2}$ .

[2]

Using the dot product calculated, determine the cosine of the angle $\theta$ between the two vectors $\mathbf{F_1}$ and $\mathbf{F_2}$ .

[3]

Determine if the angle between the two vectors is within the safe range of $30^\circ$ to $60^\circ$ .

[3]

Question 9

HLPaper 1

Consider a circle with a diameter $XY$ , where $X$ has coordinates $(1, 4, 0)$ and $Y$ has coordinates $(-3, 2, -4)$ . The circle forms the base of a right cone whose vertex $Z$ has coordinates $(-1, -1, 0)$ .

Find the coordinates of the centre of the circle.

[2]

Find the radius of the circle.

[2]

Find the exact volume of the cone.

[4]

Question 10

HLPaper 2

The points $A(5, -2, 5)$ , $B(5, 4, -1)$ , $C(-1, -2, -1)$ and $D(7, -4, -3)$ are the vertices of a right pyramid. The line $L$ passes through the point $D$ and is perpendicular to plane $\Phi$ .

Find the vectors $\overrightarrow{AB}$ and $\overrightarrow{AC}$ .

[2]

Show that the Cartesian equation of the plane $\Phi$ that contains the triangle $ABC$ is $-x+y+z=-2$ .

[3]

Find a vector equation of the line $L$ .

[1]

Hence determine the minimum distance, $d_{\text{min}}$ , from $D$ to $\Phi$ .

[4]

Use a vector method to show that $B\hat{A}C = 60^\circ$ .

[3]

Find the volume of right pyramid $ABCD$ .

[4]