RevisionDojo

D.4 Induction - IB Questionbank | RevisionDojo

Practice D.4 Induction with authentic IB Physics exam questions for both SL and HL students. This question bank mirrors Paper 1A, 1B, 2 structure, covering key topics like mechanics, thermodynamics, and waves. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.

Paper

Level

Question 1

HLPaper 2

A rectangular coil with 120 turns, length $0.10\ \text{m}$ and width $0.05\ \text{m}$ is pulled at constant velocity $2.0\ \text{m s}^{-1}$ into a uniform magnetic field of $0.40\ \text{T}$ perpendicular to the plane of the coil. It takes $0.025\ \text{s}$ for the entire coil to enter the field.

Calculate the change in magnetic flux through the coil during this interval.

[2]

Determine the average emf induced during this time.

[2]

Explain how the induced emf would change if the coil entered the magnetic field at an angle.

[2]

Question 2

HLPaper 2

A coil of wire with $N = 150$ turns is placed in a region where the magnetic flux through the coil changes uniformly from $2.0 \times 10^{-4}\ \text{Wb}$ to $0$ in $0.10\ \text{s}$ .

State Faraday’s law of electromagnetic induction.

[1]

Calculate the magnitude of the average induced emf in the coil.

[2]

Explain how Lenz’s law determines the direction of the induced emf.

[1]

Question 3

HLPaper 2

A straight conductor of length $0.50\ \text{m}$ moves at a speed of $6.0\ \text{m s}^{-1}$ perpendicular to a magnetic field of strength $0.40\ \text{T}$ .

State the condition under which a moving conductor in a magnetic field induces an emf.

[1]

Calculate the induced emf across the ends of the conductor.

[2]

Explain what would happen to the induced emf if the conductor moved parallel to the magnetic field.

[1]

Question 4

HLPaper 2

A bar of length $0.60\ \text{m}$ is placed on conducting rails connected to a resistor. The bar moves to the right at $3.0\ \text{m s}^{-1}$ through a uniform magnetic field of $0.50\ \text{T}$ directed into the page. The total resistance of the circuit is $2.0\ \Omega$ .

Calculate the emf induced across the bar.

[2]

Determine the current in the circuit.

[1]

Calculate the power dissipated in the resistor.

[1]

Explain the energy transformation taking place in this system.

[2]

Question 5

HLPaper 2

A coil with $N = 200$ turns and area $A = 0.020\ \text{m}^2$ rotates at a frequency of $f = 60\ \text{Hz}$ in a uniform magnetic field of strength $B = 0.30\ \text{T}$ . The axis of rotation is perpendicular to the magnetic field.

Calculate the maximum magnetic flux through the coil.

[1]

Determine the angular speed of the coil.

[1]

Calculate the maximum emf induced in the coil.

[2]

Explain why the induced emf is sinusoidal.

[2]

Question 6

HLPaper 2

A generator produces a sinusoidal alternating voltage. The graph below shows the variation of the output voltage $V$ with time $t$ .

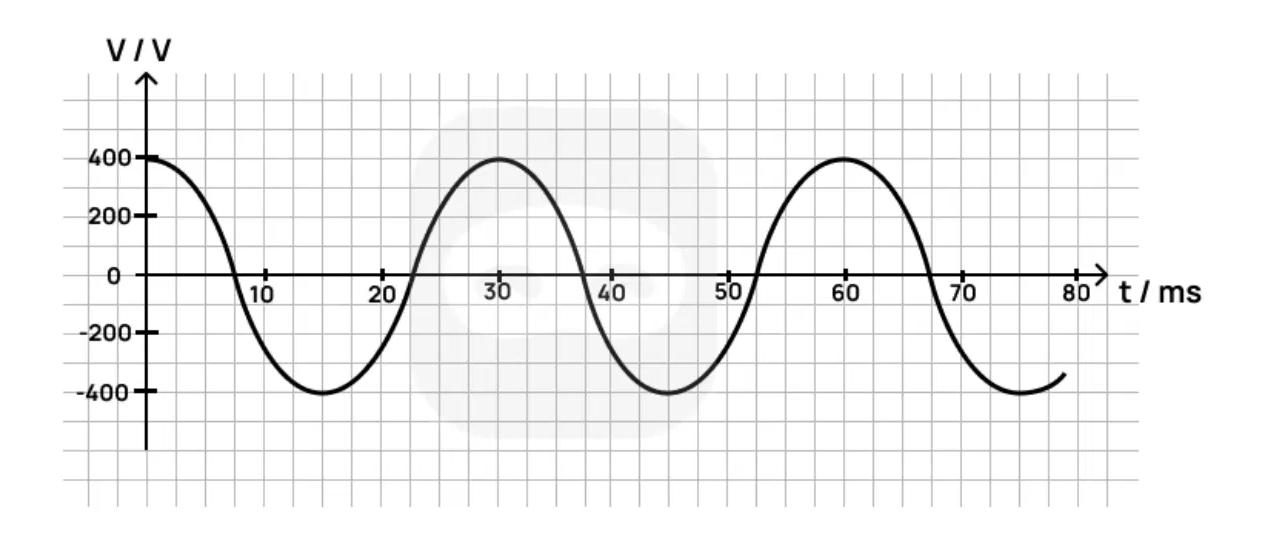
Calculate the frequency of the alternating voltage.

[1]

Calculate the root mean square (rms) value of the voltage.

[1]

The generator supplies this voltage to a resistive load of resistance 50 $\Omega$ . Calculate the average power dissipated in the load.

[2]

Sketch a graph of the variation of the instantaneous power with time over one full cycle. Clearly label peak power and time axis values.

[2]

Discuss how the rotation of a coil in a magnetic field leads to the voltage output shown in the graph. In your answer, refer to magnetic flux, Faraday's law, and the shape of the output.

[3]

Question 7

HLPaper 2

A magnet oscillates vertically above a stationary circular coil with $N = 200$ turns and radius $0.10\ \text{m}$ . The magnetic field at the centre of the coil due to the magnet varies sinusoidally with time as $B(t) = 0.30 \sin(120\pi t)\ \text{T}$ .

Calculate the magnetic flux through the coil as a function of time.

[2]

Determine the emf induced in the coil as a function of time.

[2]

Calculate the maximum induced emf in the coil.

[1]

Explain how this setup demonstrates Lenz’s law and conservation of energy.

[2]

Question 8

HLPaper 2

The diagram shows a conducting rod of length $L$ sliding to the right with constant velocity $v$ along two parallel conducting rails in a uniform magnetic field directed into the page. The system is part of a closed rectangular circuit.

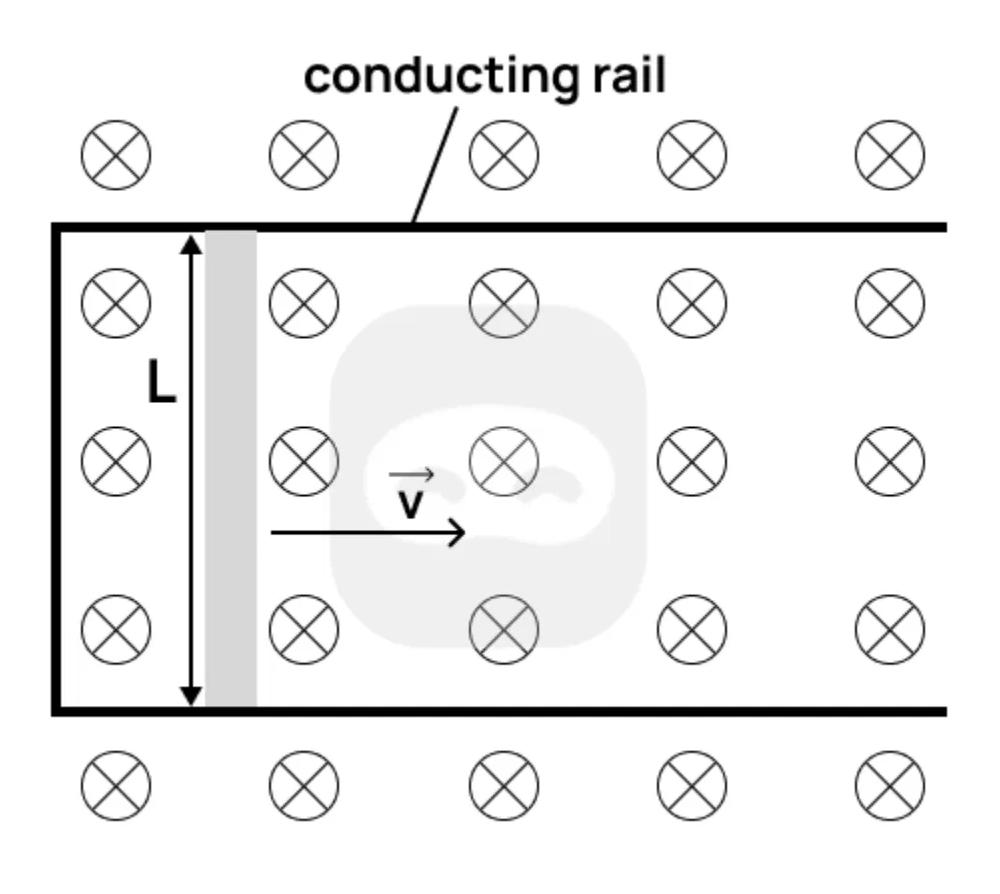
State the direction of the induced current in the circuit.

[1]

Explain the physical origin of the induced emf in the rod.

[2]

Outline an expression for the induced emf $\mathcal{E}$ across the ends of the moving rod.

[1]

Given $L = 0.30 \ \text{m}$ , $v = 5.0 \ \text{m s}^{-1}$ , and $B = 0.80 \ \text{T}$ , calculate the magnitude of the induced emf.

[2]

If the resistance of the circuit is $0.20 \ \Omega$ , determine the current in the circuit and the power delivered by the magnetic force keeping the rod moving at constant speed.

[2]

Question 9

HLPaper 2

A rectangular coil of $N = 250$ turns, each of area $A = 0.015\ \text{m}^2$ , rotates in a uniform magnetic field $B = 0.40\ \text{T}$ with an angular frequency $\omega = 400\ \text{rad s}^{-1}$ .

Calculate the maximum magnetic flux through the coil.

[1]

Determine the peak emf induced in the coil.

[2]

Write the expression for the emf as a function of time.

[1]

Explain the effect on the induced emf if the number of turns is doubled and the angular frequency is halved.

[2]

Question 10

HLPaper 2

A coil with 150 turns and cross-sectional area $2.5 \times 10^{-3}\ \text{m}^2$ rotates in a uniform magnetic field of $0.20\ \text{T}$ according to $\theta(t) = \omega t$ , where $\omega = 500\ \text{rad s}^{-1}$ .

Calculate the magnetic flux through the coil as a function of time.

[1]

Determine the expression for the induced emf as a function of time.

[2]

Calculate the maximum emf induced in the coil.

[1]

Explain how increasing the frequency of rotation affects the shape and amplitude of the emf.

[2]

Topic A - Space, time and motion5 subtopics

Topic B - The particulate nature of matter5 subtopics

Topic C - Wave behaviour5 subtopics

Topic D - Fields4 subtopics

Topic E - Nuclear and quantum physics5 subtopics

D.4 Induction Questionbank