Practice D.2 Electric and magnetic fields with authentic IB Physics exam questions for both SL and HL students. This question bank mirrors Paper 1A, 1B, 2 structure, covering key topics like mechanics, thermodynamics, and waves. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
Two point charges, and , are separated by a distance of .
Calculate the electric potential at a point P located from and from .
Determine the work done to bring a charge from infinity to point P.
Calculate the electric field strength at point P due to each charge and determine the net electric field vector at point P. (Assume the geometry places the field vectors at to one another.)
Find the magnitude of the net electric field at point P.
Explain why the direction of the electric field is not the same as the direction of the electric potential gradient in this case.
An electron is accelerated from rest through a potential difference of and enters a region of uniform magnetic field of strength directed perpendicular to its velocity. Charge of electron , mass .
Calculate the speed of the electron just before it enters the magnetic field.
Determine the radius of its circular path in the magnetic field.
Calculate the frequency of revolution of the electron.
Calculate the number of revolutions the electron completes in .
Describe qualitatively what would happen to the electron’s trajectory if the magnetic field strength were gradually increased.
The diagram shows a proton and an electron placed between two parallel plates. The upper plate is positively charged, and the lower plate is negatively charged. The separation between the plates is , and the electric field is uniform.
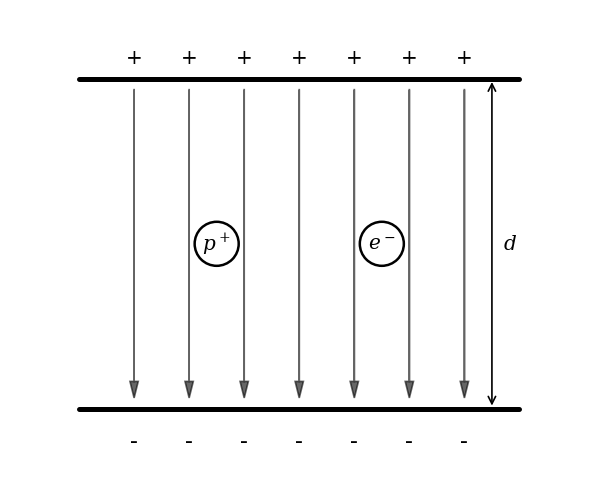
State the direction of the electric field between the plates.
State the direction of the electric force on the proton and the electron.
Identify the magnitudes of the electric force on the proton and the electron.
Deduce the accelerations of the proton and the electron.
A conducting sphere of radius carries a charge of .
Calculate the electric potential at the surface of the sphere.
Determine the electric field strength just outside the surface of the sphere.
A charge of is brought from infinity to the surface of the sphere. Calculate the work done by the electric field.
Explain the shape and spacing of equipotential surfaces around the sphere.
Discuss the relationship between the gradient of electric potential and the electric field in this context.
The diagram shows a set of electric field lines around an unknown charge distribution. The arrows indicate the direction of the electric field. Two points, X and Y, are marked within the field.
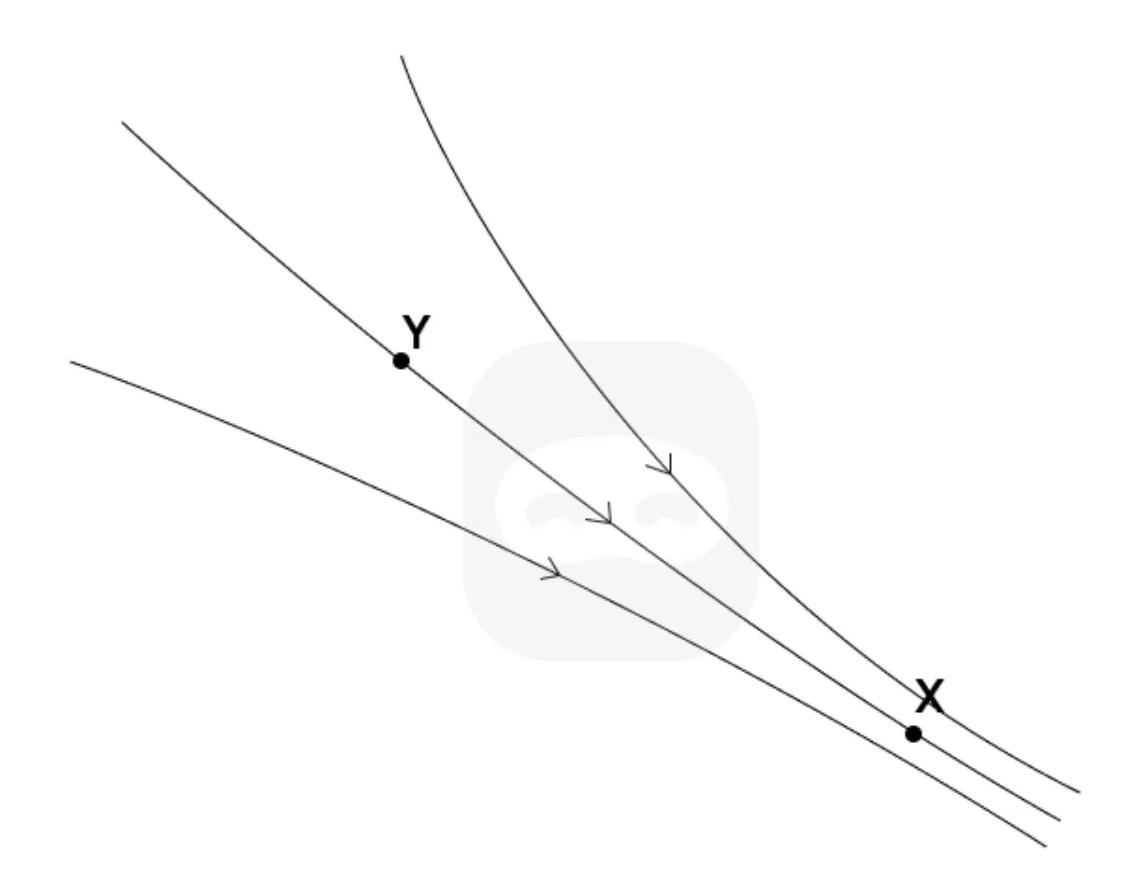
State the direction of the electric field at point X.
Describe the electric field strength at points X and Y.
Outline how the electric potential at X compares to that at Y.
Describe the motion of a positive test charge initially at rest at point Y.
Two point charges, and , are fixed in place apart in vacuum.
Determine the point along the line joining the charges where the electric potential is zero.
Explain whether the electric field is also zero at this point.
Calculate the electric field strength at a point located to the left of .
Use the electric potential gradient to calculate the field strength between two points apart in the region between the charges, where the potential changes from to .
Sketch a graph of electric potential as a function of distance along the line connecting the charges. Indicate regions of steepest slope and relate them to field strength.
A point charge is located at the origin. A test charge is moved from point A at to point B at from the origin, along the radial direction.
Calculate the electric potential at points A and B.
Determine the work done by the electric field in moving the test charge from A to B.
Calculate the change in electric potential energy of the test charge.
Use the electric potential gradient to estimate the average electric field strength between points A and B.
Describe the relationship between electric field lines and equipotential surfaces in this configuration.
The diagram shows a particle of mass and charge in uniform circular motion around a fixed point charge . The particle moves at constant speed in a circular orbit of radius due to the electrostatic force of attraction between the charges.
State the direction of the electrostatic force acting on the orbiting particle and explain its role in the motion.
Deduce an expression for the speed of the orbiting particle in terms of , , , and fundamental constants.
Show that the total energy (kinetic + potential) of the orbiting particle is negative, and explain its physical significance.
An electron is released from rest in a uniform electric field of strength . The charge of an electron is and its mass is .
State the direction of the acceleration of the electron.
Calculate the magnitude of the force acting on the electron.
Determine the acceleration of the electron.
The diagram shows a negatively charged particle placed midway between two oppositely charged parallel plates. The plates are separated by a distance and create a uniform electric field.
State the direction of the electric field between the plates.
Identify the direction of the electric force acting on the particle.
Outline what happens to the motion of the particle after it is released from rest.
Describe how the electric field strength would change if the distance between the plates were increased but the potential difference remained constant.