Practice Topic C - Wave behaviour with authentic IB Physics exam questions for both SL and HL students. This question bank mirrors Paper 1A, 1B, 2 structure, covering key topics like mechanics, thermodynamics, and waves. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
Paper
Level
Question 1
SLPaper 2
A tube is closed at one end and open at the other.
1.[2]
Draw the fundamental mode of the standing wave in the tube.
2.[1]
State the position of the node and antinode.
3.[1]
State the length of the tube in terms of the wavelength.
Question 2
HLPaper 2
A block of mass is attached to a spring with a spring constant and oscillates on a frictionless surface. The maximum displacement from equilibrium is .
1.[2]
Calculate the angular frequency of the motion.
2.[2]
Determine the maximum speed of the block.
3.[1]
Calculate the maximum kinetic energy of the block.
4.[2]
Determine the speed of the block when it is from the equilibrium position.
5.[1]
Explain why the potential and kinetic energy vary during the motion, even though their sum remains constant.
Question 3
HLPaper 2
A stationary ambulance emits a siren at a frequency of . An observer stands some distance in front of the ambulance.
1.[1]
State what is meant by the Doppler effect.
2.[2]
Calculate the observed frequency if the ambulance moves toward the observer at and the speed of sound is .
3.[1]
Explain whether the observed frequency would be higher or lower if the observer were moving toward the ambulance.
Question 4
HLPaper 2
A spacecraft moves directly toward a space station at and emits a radio signal with a rest frequency of . The frequency of the signal received by the space station is approximately .
1.[2]
Determine the observed wavelength of the signal on the space station.
2.[2]
Explain why the relativistic formula must be used instead of the classical one.
Question 5
SLPaper 2
The diagram shows a stationary observer while a loudspeaker moves toward them, emitting a constant sound. The observer hears a change in the pitch of the sound due to the relative motion of the source.
1.[1]
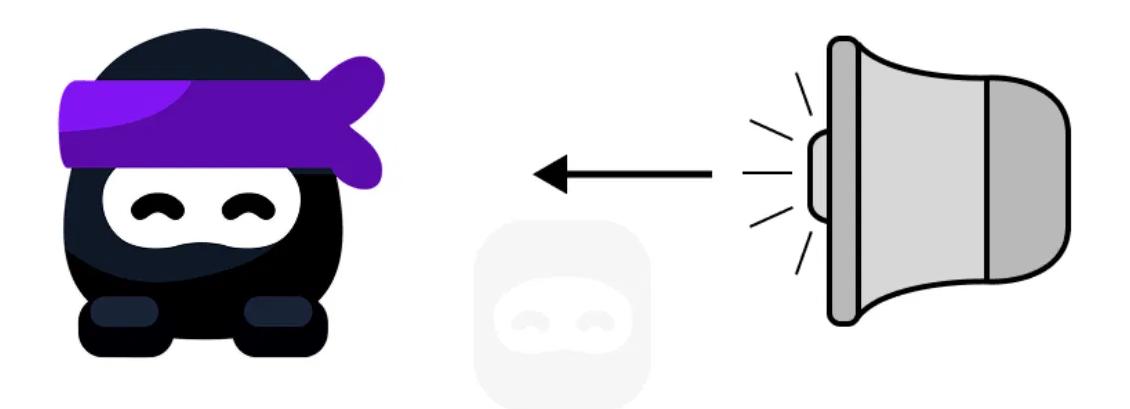
State what happens to the frequency of the sound as heard by the observer.
2.[2]
Outline why this change in frequency occurs.
3.[1]
Suggest what would be heard if the source were moving away from the observer instead.
4.[2]
Describe one real-life situation in which this Doppler effect can be experienced.
Question 6
SLPaper 2
The diagram shows a loudspeaker moving away from a stationary observer. The loudspeaker emits a constant tone, but the observer hears a change in the sound due to the Doppler effect.
1.[1]
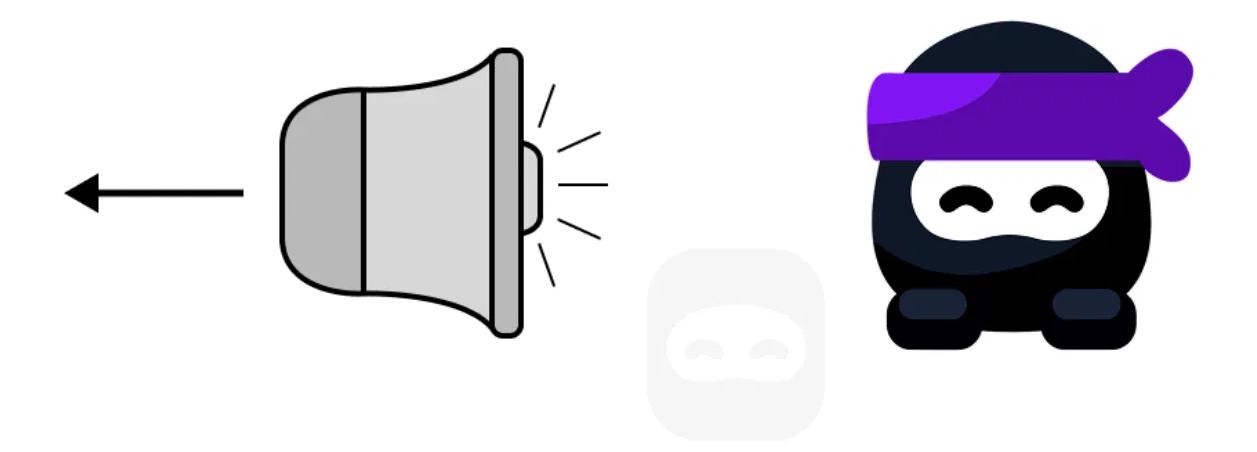
State what happens to the frequency of the sound as heard by the observer.
2.[2]
Outline why this change in frequency occurs.
3.[1]
Suggest what would happen to the pitch of the sound if the source stopped moving.
4.[2]
Describe one real-life situation where a similar Doppler effect can be observed.
Question 7
SLPaper 2
The graph shows the displacement-time representation of two transverse waves (solid and dashed) travelling through the same medium. Both waves have the same amplitude and frequency.
1.[1]
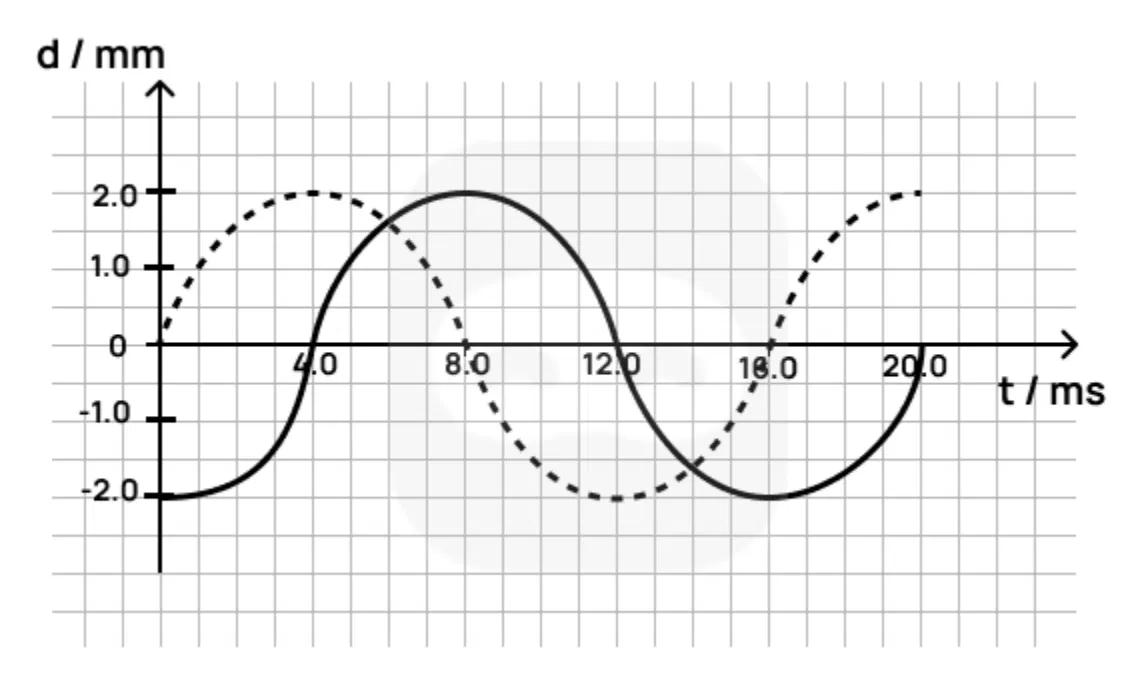
State the amplitude of either wave.
2.[2]
Determine the period of the waves.
3.[2]
Determine the phase difference between the two waves.
4.[1]
Outline one difference between the two waves other than phase.
5.[2]
Explain how the principle of superposition is used to determine the resultant displacement of these waves at any time .
Question 8
SLPaper 2
Two waves of equal amplitude and frequency travel in opposite directions along a string fixed at both ends.
1.[2]
Explain how a standing wave is formed.
2.[2]
Describe the difference between nodes and antinodes in a standing wave.
3.[2]
A standing wave with three antinodes forms on a string of length . Calculate the wavelength of the wave.
4.[2]
The wave has a frequency of . Determine the speed of the wave on the string.
5.[2]
Sketch the wave pattern on the string, labeling the position values of all nodes and antinodes along the length of the string.
Question 9
SLPaper 2
A ripple tank is used to demonstrate wave behaviour. Straight water waves are directed towards a barrier with a small gap in it.
1.[2]
Describe the diffraction pattern observed when the gap width is smaller than the wavelength of the incident waves.
2.[1]
Suggest how the diffraction pattern changes as the gap becomes significantly wider than the wavelength.
3.[2]
Explain how the degree of diffraction depends on the relationship between wavelength and gap width.
4.[2]
State one similarity and one difference between diffraction of light and water waves.
5.[3]
Discuss how diffraction experiments provide evidence for the wave model of light.