Practice Topic B - The particulate nature of matter with authentic IB Physics exam questions for both SL and HL students. This question bank mirrors Paper 1A, 1B, 2 structure, covering key topics like mechanics, thermodynamics, and waves. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
A sealed container holds a fixed mass of gas at constant temperature. The volume of the gas is reduced from to .
State the gas law that applies to this situation.
If the initial pressure is , calculate the final pressure.
Explain why the pressure increases as the volume decreases.
A cylinder of height contains a fixed mass of ideal gas. A piston is used to compress the gas isothermally (at constant temperature ). The initial volume and pressure of the gas are and respectively. After compression, the piston is located at height , so the gas occupies only of its original volume.
Assume the cross-sectional area of the cylinder remains constant throughout the process.
State the ideal gas law.
Outline two assumptions of the ideal gas model.
State the ratio of the volumes of the gas before () and after () compression.
The temperature of the gas remains constant at . Using the ideal gas law, determine the ratio where is the pressure after compression.
Explain why, during this isothermal compression, work is done on the gas.
The gas is then heated at constant volume until its pressure reaches . Determine the final temperature in terms of the initial temperature .
A gas is trapped in a cylinder with a movable piston. The gas is slowly heated, and its volume is observed to increase while the pressure remains constant.
State the gas law that describes this behaviour.
If the initial volume is at , calculate the new volume when the temperature is increased to .
Explain the relationship between temperature and volume in this context.
The diagram shows a cyclic process for a fixed amount of an ideal gas undergoing four steps.
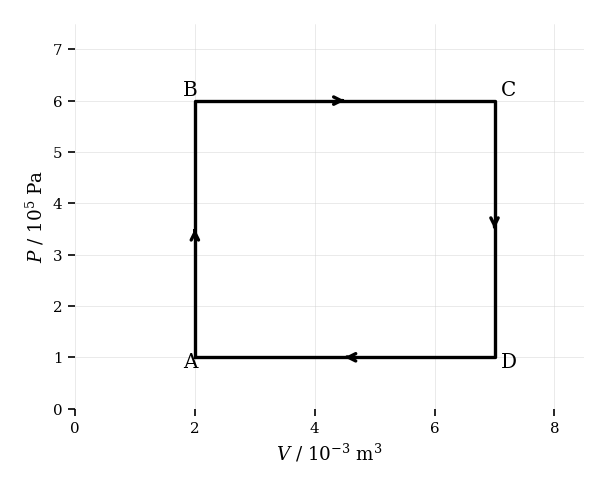
Describe the temperature changes along each segment of the cycle.
Calculate the work done by the gas during the segment .
Determine the net work done over the complete cycle.
Outline whether the gas does net positive or negative work over the full cycle, based on the diagram.
A sample of an ideal monatomic gas is at a pressure of and a volume of . The molar mass of the gas is .
Calculate the number of moles of gas in the sample.
Determine the temperature of the gas.
Calculate the total internal energy of the gas.
Explain why the internal energy of a monatomic ideal gas is entirely kinetic.
Two rigid containers are connected by a closed valve.
- The left container has volume and contains gas at pressure and temperature .
- The right container has volume and contains gas at pressure and the same temperature .
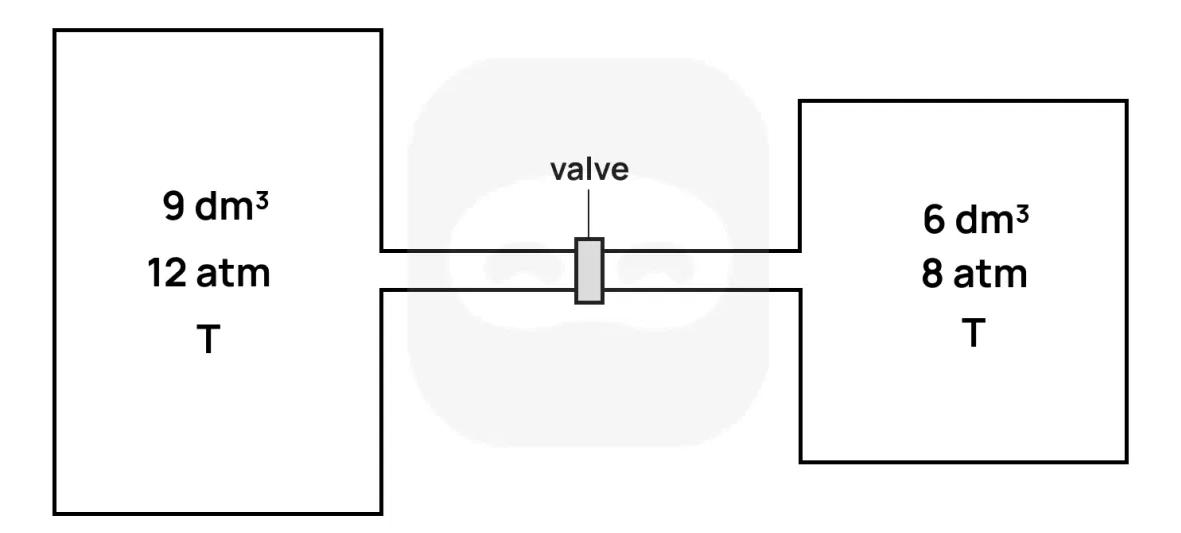
The valve is then opened and the gases are allowed to mix and reach equilibrium. Assume temperature remains constant and the gases are ideal and non-reactive.
State the ideal gas law.
Determine an expression for the number of moles in each container before the valve is opened, in terms of and .
Determine an expression for the total number of moles in the system.
Calculate the final equilibrium pressure of the system after the valve is opened.
Suggest why temperature must remain constant for this pressure calculation to be valid.
The diagram below represents an ideal and monatomic gas that first undergoes a compression, followed by an increase in pressure.
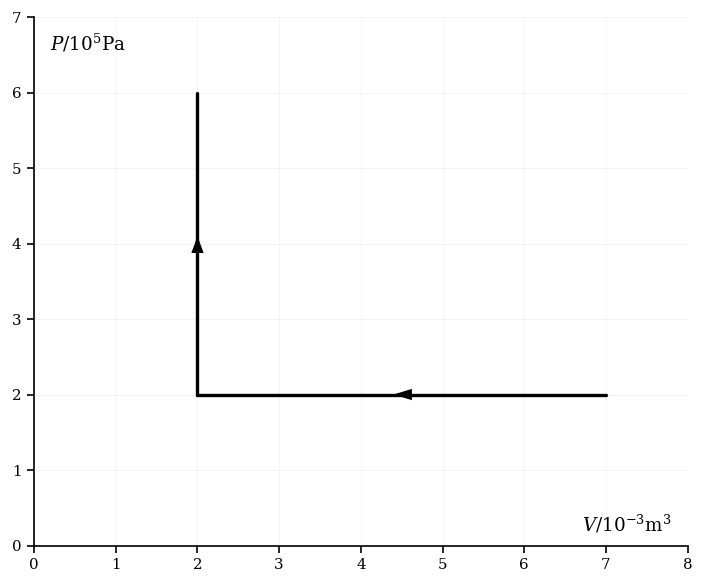
Calculate the work done during the compression.
Calculate the work done during the increase in pressure.
An adiabatic process then increases the volume of the gas to . Calculate the pressure following this process.
Outline how you can achieve an approximate adiabatic change in practice.
A black metal plate and a shiny metal plate are both placed under direct sunlight. After some time, the black plate is noticeably warmer than the shiny plate.
Explain why the black plate heats up more quickly than the shiny plate when exposed to sunlight.
If both plates are then moved to a shaded area, explain how the color and surface properties of each plate affect how quickly they lose heat.
A gas expands adiabatically. A student records its pressure and volume and plots the graph below:
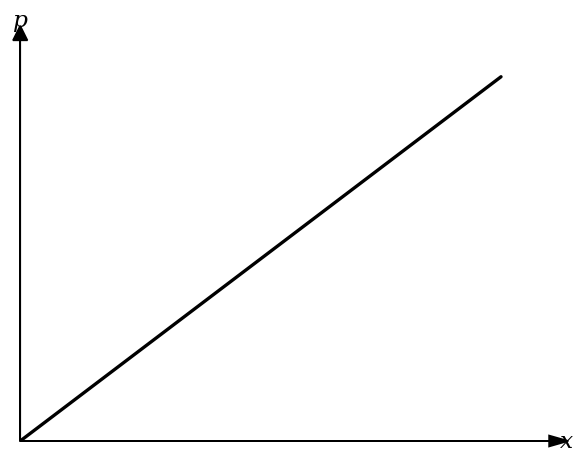
What is the most likely quantity on the x-axis?
A planet has albedo 0.25, emissivity 0.6, and solar constant .
Calculate the mean absorbed intensity.
Write the energy balance equation and estimate the surface temperature.
Outline the effect of increasing albedo on the temperature.