Practice D.3 Motion in electromagnetic fields with authentic IB Physics exam questions for both SL and HL students. This question bank mirrors Paper 1A, 1B, 2 structure, covering key topics like mechanics, thermodynamics, and waves. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
Paper
Level
Question 1
SLPaper 2
A proton enters a region of space where there is a uniform magnetic field of strength directed into the page. The proton travels in a circular path of radius .
1.[2]
Calculate the speed of the proton in the magnetic field.
2.[2]
Determine the kinetic energy of the proton.
3.[1]
Outline one method by which the proton could have been accelerated to this speed.
4.[2]
Explain why the magnetic field does no work on the proton.
5.[1]
Suggest why electrons moving with the same speed in the same magnetic field are deflected more than protons.
Question 2
SLPaper 2
A uniform magnetic field is applied perpendicular to the direction of motion of an electron beam in a cathode ray tube. The electrons follow a semicircular path before striking a fluorescent screen.
1.[1]
State the nature of the magnetic force acting on a moving charge.
2.[2]
Describe the motion of an electron in a magnetic field when it enters at right angles to the field lines.
3.[2]
Calculate the time taken for an electron moving at to complete a semicircular path of radius m.
4.[3]
Determine the magnetic field strength if the radius of the path is m and the speed of the electron is as given in Part 3.
5.[1]
Suggest why a semicircular path is preferable in this setup compared to a full circular path.
Question 3
SLPaper 2
The diagram shows a positively charged particle with charge moving in a circular path in a region where the magnetic field is uniform and directed out of the page.
1.[1]
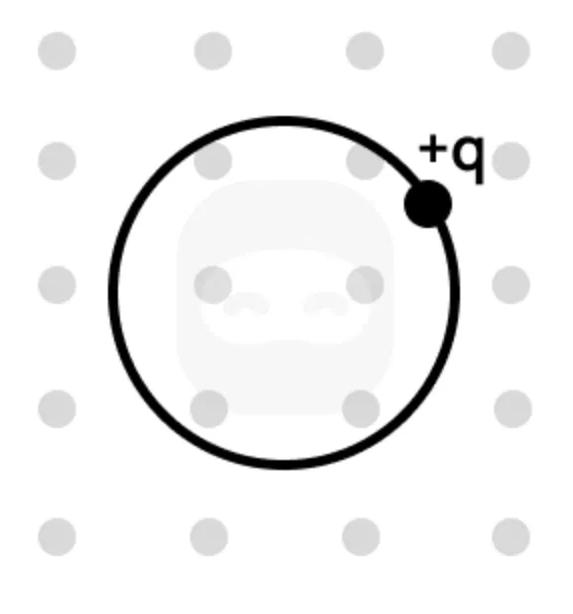
State the direction of the magnetic force acting on the particle at the position shown.
2.[2]
Outline why the particle moves in a circular path in this magnetic field.
3.[1]
State what would happen to the radius of the path if the speed of the particle were increased.
4.[1]
Identify one other factor (besides speed) that affects the radius of the particle's circular path.
Question 4
SLPaper 2
The diagram shows a proton entering a uniform electric field between two oppositely charged parallel plates. The electric field is directed vertically downward, and the proton enters with an initial velocity at an angle of above the horizontal.
1.[1]
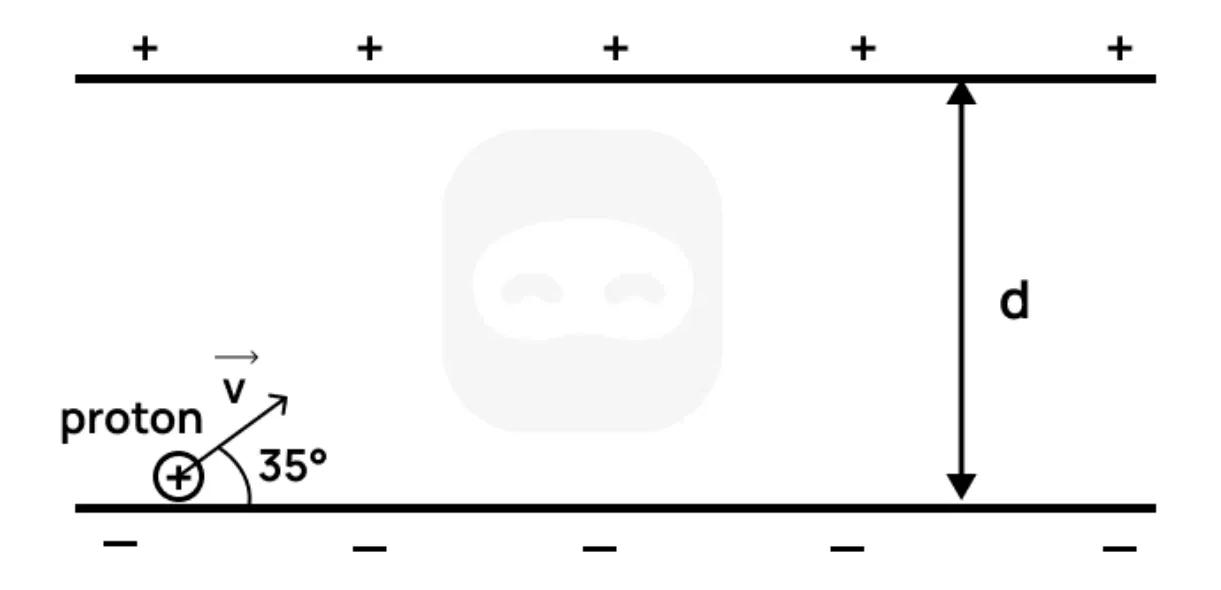
State the direction of the electric force acting on the proton.
2.[2]
Describe the path followed by the proton as it moves through the field.
3.[2]
Outline how the vertical and horizontal components of the proton's velocity affect its trajectory.
4.[1]
Suggest one change to the setup that would increase the vertical deflection of the proton.
Question 5
SLPaper 2
In an experimental setup, electrons are accelerated and injected into a region with a uniform magnetic field. The electrons move in a circular orbit, and their electromagnetic radiation (emitted due to their acceleration) is measured. The experiment is conducted under ultra-high vacuum to avoid particle interactions with air molecules.
1.[2]
Explain why electrons in circular motion within a magnetic field are accelerating, even if their speed is constant.
2.[2]
A beam of electrons is moving perpendicular to a uniform magnetic field of magnitude . The speed of each electron is .
Determine the radius of the electron’s orbit under these conditions.
3.[2]
Describe the effect on the radius of the electron’s path if the speed of the electron is increased.
Question 6
SLPaper 2
A beam of protons is accelerated from rest through a potential difference and then injected into a region of space where a uniform magnetic field and a uniform electric field are present. The magnetic field is directed out of the page, and the proton beam enters the region travelling horizontally to the right.
1.[2]
Calculate the speed of the protons after being accelerated through a potential difference of .
2.[3]
Determine the magnitude and direction of the electric field required to allow the protons to move undeflected through a magnetic field of strength .
3.[1]
Deduce the expression for the radius of curvature of the protons' path if the electric field is turned off and only the magnetic field acts.
4.[2]
Calculate the radius of the circular path under the conditions in Part 3.
5.[3]
Discuss how this system could be used to select particles of a specific velocity, and how this relates to the principle of a velocity selector in a mass spectrometer.
Question 7
SLPaper 2
A positively charged particle enters a region with perpendicular electric and magnetic fields. The fields are adjusted such that the particle continues in a straight-line path without deflection.
1.[2]
Describe the forces acting on the charged particle in the region of crossed fields.
2.[1]
Write an equation for the condition required for the particle to move undeflected through the region.
3.[2]
Calculate the speed of a particle that moves undeflected when the electric field strength is and the magnetic field strength is .
4.[3]
Determine the radius of the circular path of the particle after it exits the region of the electric field and enters a region with only the magnetic field, assuming it continues with the same speed. The particle has mass and charge .
5.[2]
Explain why this setup is useful for velocity selection in a mass spectrometer.
Question 8
SLPaper 2
The diagram shows a positively charged particle with charge moving in a uniform magnetic field directed into the page. The particle follows a circular path.
1.[1]
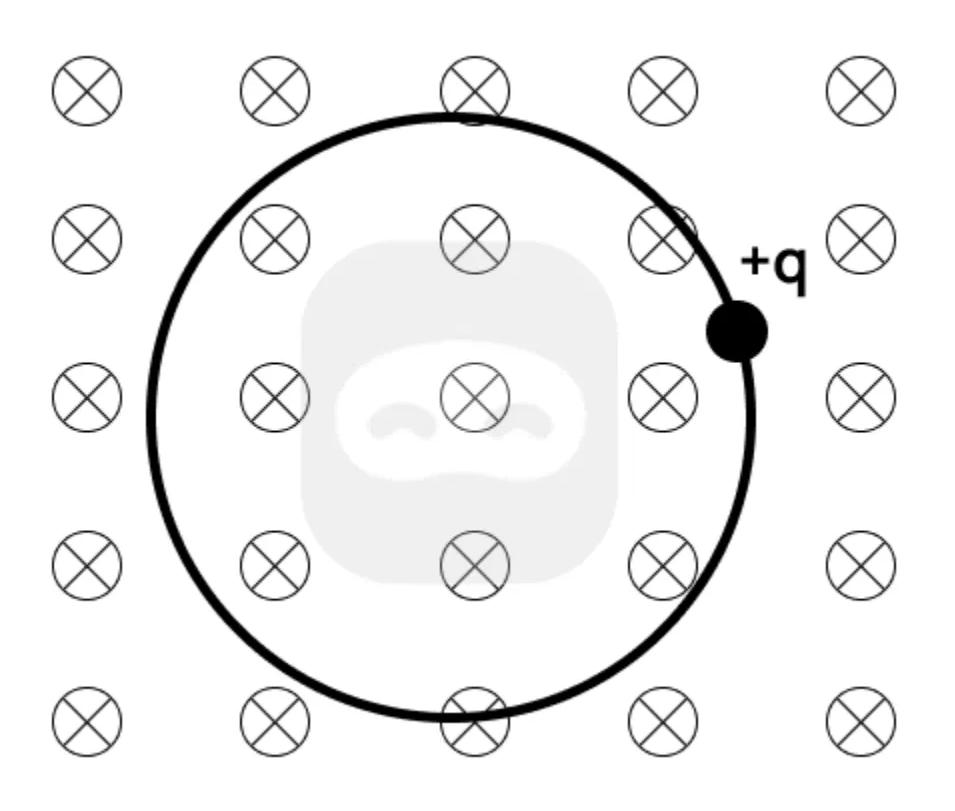
State the direction of the magnetic force acting on the particle at the instant shown.
2.[2]
Outline the reason why the particle moves in a circular path.
3.[1]
State what would happen to the radius of the circular path if the particle's speed were increased.
4.[2]
Identify two factors, other than speed, that affect the radius of the circular path.
Question 9
SLPaper 1A
A wire of length carries a current of perpendicular to a uniform magnetic field of . If the wire is suspended horizontally and remains motionless, what is the minimum mass that the wire must have per unit length?
Question 10
SLPaper 1A
The diagram shows a current-carrying wire placed in a uniform magnetic field directed into the page. The current flows to the right.
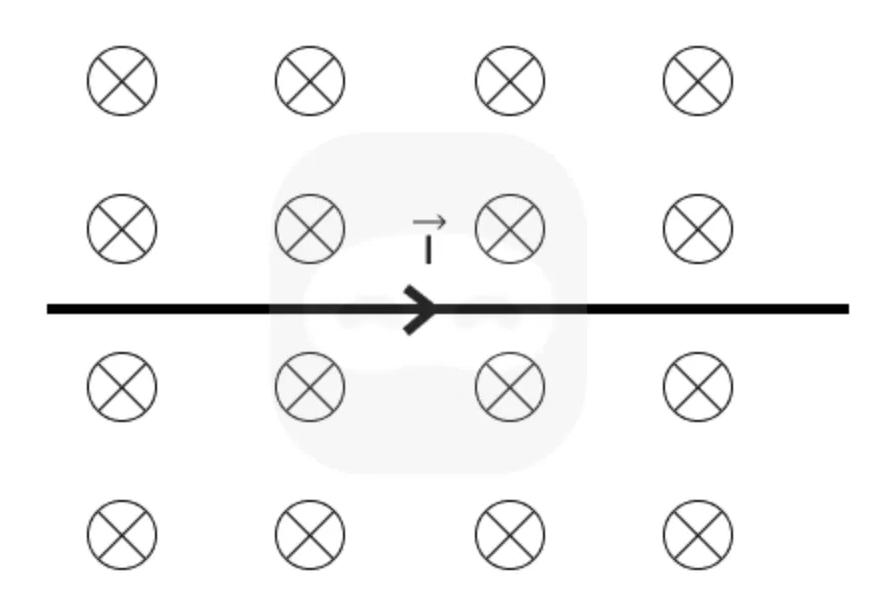
What is the direction of the magnetic force acting on the wire?