Practice A.5 Galilean and special relativity (HL only) with authentic IB Physics exam questions for both SL and HL students. This question bank mirrors Paper 1A, 1B, 2 structure, covering key topics like mechanics, thermodynamics, and waves. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
A radio station measures a passing spaceship to be in length. If the captain travelling on that spaceship measures the spaceship to be in length, what speed is the spaceship travelling at?
An observer in inertial frame sees a particle moving in the direction at a constant speed of , where .
The particle decays after a proper lifetime of .
Calculate the time taken for the particle to decay in frame .
Hence, how far does the particle travel in frame before decaying?
Calculate the space-time interval between the particle's creation and decay in .
Determine the coordinates of the decay event in the particle's rest frame .
Explain why the distance travelled by the particle in its rest frame is zero, even though it appears to travel in .
An observer on Earth sees a spaceship of proper length pass by at a speed such that its observed length is . How much time elapses on the spaceship clock during the time it takes to fully pass a fixed point on Earth (according to the spaceship)?
Weiran reports that an event occurred on the x-axis of her reference frame at at time . Nicole and her frame are moving in the negative direction of the x-axis at a speed of . Nicole passes Weiran at t=0. What are the spatial and temporal coordinates of the event according to Nicole?
| Spatial Coordinate | Temporal Coordinate | |
|---|---|---|
| A | ||
| B | ||
| C | ||
| D |
Two events occur apart and apart in time in some inertial frame. What is the relative speed of a frame in which the two events are simultaneous?
A spaceship flies past a space station at . According to observers on the station, a clock on the spaceship ticks once every .
What is the time interval between ticks in the spaceship's own frame?
A spaceship moves at a speed of relative to Earth. A light pulse is emitted from the rear of the spaceship and travels toward the front. The spaceship has a proper length of .
Calculate the time it takes for the light to reach the front of the spaceship as measured by an observer on the spaceship.
Determine the length of the spaceship as measured by the Earth observer.
Calculate the time it takes for the light to reach the front of the spaceship as measured by the Earth observer.
Explain why the time intervals calculated in Part 1 and Part 3 differ, and relate this to the principle of relativity of simultaneity.
On the following spacetime diagram, is the world line of a spacecraft and is the space axis of its reference frame. Two photons, X and Y, are emitted towards the spacecraft. The emission and the world line of each photon is shown on the diagram.
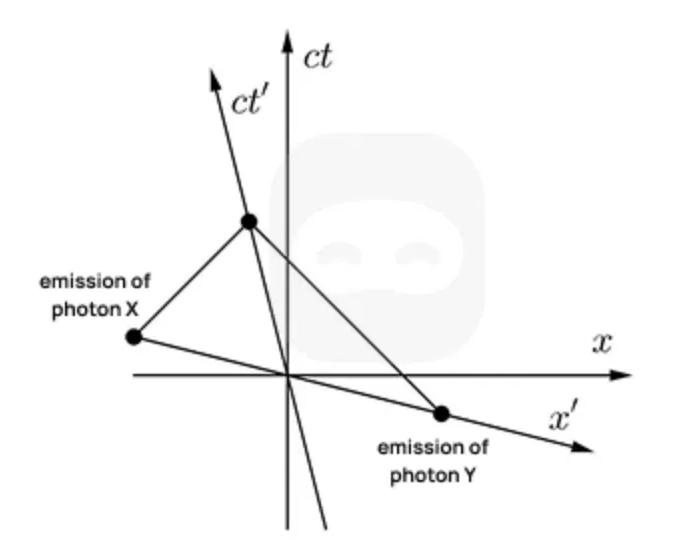
Which of the following statements is correct in the reference frame of the spacecraft?
A muon travelling at penetrates the Earth's upper atmosphere. If muons have a half-life of in their rest frame, how far would the muon travel in Earth's reference frame before decaying?
A space probe moves at relative to Earth towards it. A signal is sent from Earth to the probe. In the Earth's frame, the probe is away from the Earth when the signal is transmitted.
Calculate the time it takes for the probe to receive the signal, according to the Earth's frame.
Assume the signal travels at the speed of light, .
Determine the position and time of signal reception in the Earth frame.
Determine the Lorentz factor for the inertial frame transformation from the Earth’s rest frame to that of the probe.
Hence, use Lorentz transformations to calculate the time and location of signal reception in the probe's rest frame.
Discuss how this demonstrates the relativity of simultaneity between the two frames.