Practice A.1 Kinematics with authentic IB Physics exam questions for both SL and HL students. This question bank mirrors Paper 1A, 1B, 2 structure, covering key topics like mechanics, thermodynamics, and waves. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
A sledge carrying a box slides down a smooth snow slope, starting from rest at the top. The slope curves smoothly until it becomes horizontal, as shown.
Assume there is no friction between the sledge and the snow. Air resistance is negligible.
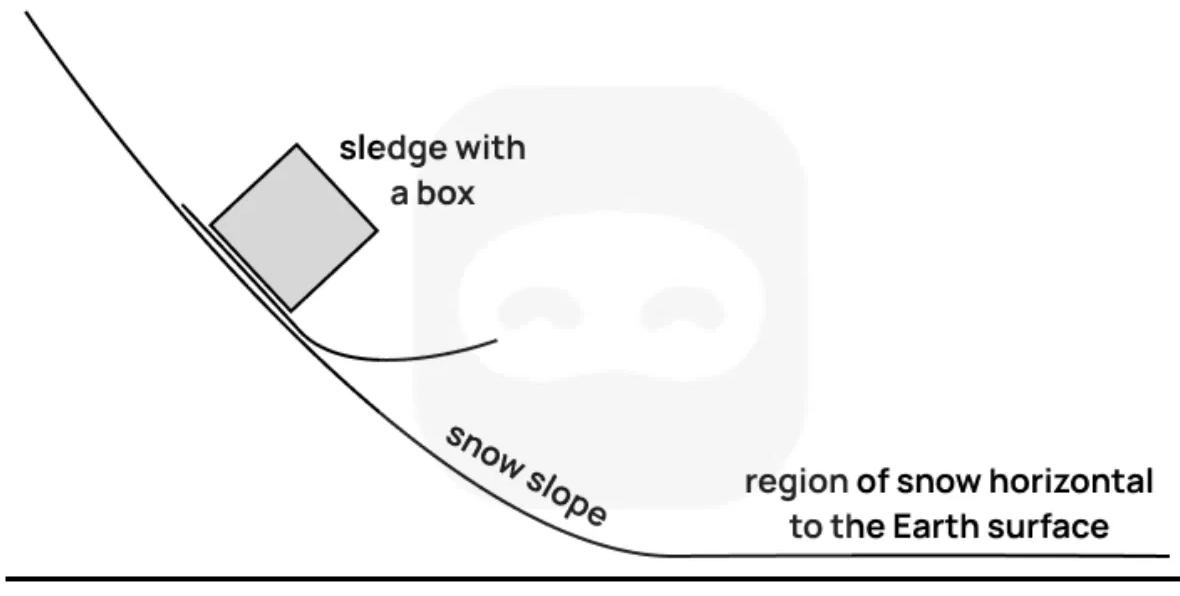
State the energy transformations taking place as the sledge descends the slope.
The sledge and box together have a mass .
At the top of the slope, the sledge is at a vertical height above the horizontal surface. Determine an expression for the speed of the sledge when it reaches the horizontal snow region.
Explain why the normal force exerted by the snow changes as the sledge moves down the curved part of the slope.
After reaching the horizontal region, the sledge travels a distance before coming to rest. The coefficient of dynamic friction between the sledge and the snow in this region is . Draw a free-body diagram showing the forces acting on the sledge while it is moving horizontally.
Determine an expression for the distance in terms of , and .
A rock is projected at an angle of above the horizontal with a speed of . Assume air resistance is negligible.
Calculate the time taken for the rock to reach the highest point of its trajectory.
Determine the maximum height reached above the point of launch.
Calculate the total horizontal distance travelled by the rock before it hits the ground.
Explain why the vertical and horizontal motions of the rock can be treated independently.
A cyclist travels along a straight road. She accelerates uniformly from rest to a speed of in .
Calculate the cyclist's acceleration.
Calculate the distance travelled by the cyclist during this acceleration.
The cyclist continues at a constant speed of for . Calculate the total distance travelled from the start to the end of this constant speed period.
Sketch a speed–time graph of the motion from the start until the end of the constant speed period.
A car accelerates uniformly from rest along a straight road. After , it reaches a speed of . It then continues at this speed for before decelerating uniformly to a stop in .
Calculate the car's acceleration during the first .
Determine the total distance travelled during the entire motion.
Sketch an acceleration–time graph for the full motion of the car.
Suggest why the graph of velocity against time is useful for calculating the distance travelled.
A delivery drone follows a predetermined route over a city: The drone starts from point O and flies 10 km north to point A. From point A, it changes direction and flies 6 km due west to point B. After reaching point B, the drone flies 8 km south to point C. Finally, the drone flies 5 km east back to point D.
Determine the total distance the drone travels during the entire journey.
Calculate the drone’s net displacement from point O to point D, both in magnitude and direction.
What is the displacement from point A to point C in terms of both magnitude and direction?
If the drone completes the route in 1 hour and 15 minutes, calculate its average speed and average velocity.
Compare the direction of the net displacement from O to D to due north.
Explain how the distance travelled and the net displacement provide different information about the drone’s journey.
If the drone needed to return directly to point O from point D, what would be the required distance and direction?
Two players are engaged in a game of table tennis. Player A strikes the ball at a height of 0.27 m above the table's surface, measured from the tabletop to the bottom of the ball. The ball's initial velocity is 13.5 m/s in the horizontal direction.
Assume that air resistance is negligible.
The ball bounces and then reaches a peak height of 0.19 m above the table with a horizontal speed of 11.2 m s. The mass of the ball is 3.6 g.
Show that the time taken for the ball to reach the surface of the table is about 0.2 s.
Sketch, on the axes provided below, a graph showing the variation with time of the vertical component of velocity of the ball until it reaches the table surface. Take to be
The net is stretched across the middle of the table. The table has a length of 4.84 m and the net has a height of 9.8 cm.
Show that the ball will go over the net.
Player B intercepts the ball at its highest point. Holding the paddle stationary in a vertical position, Player B makes contact with the ball for 0.010 s. Assume the collision is perfectly elastic.
Calculate the average force exerted by the ball on the paddle. State your answer to an appropriate number of significant figures.
Determine the kinetic energy of the ball immediately after the bounce.
A mango falls from a tree branch and takes to hit the ground. From what height did it fall?
Two stones are dropped from the same height. The second is dropped after the first. How far below the first is the second stone when the first hits the ground after it was dropped?
A ball is projected horizontally from a height of and lands away from the base of the cliff. What is the magnitude of its initial velocity?
A missile has a speed of at the top of its trajectory. Given that the missile was shot at , what angle to the horizontal was it shot at?