RevisionDojo

SL 4.6—Combined, mutually exclusive, conditional, independence, prob diagrams - IB Questionbank | RevisionDojo

Practice SL 4.6—Combined, mutually exclusive, conditional, independence, prob diagrams with authentic IB Mathematics Analysis and Approaches (AA) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like functions and equations, calculus, complex numbers, sequences and series, and probability and statistics. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.

Paper

Level

Question 1

SLPaper 2

A store sells two types of coffee: Arabica and Robusta. The probability that a customer buys Arabica is $\frac{3}{5}$ . If a customer buys Arabica, the probability they purchase a large size is $\frac{2}{3}$ . If they buy Robusta, the probability they purchase a large size is $\frac{1}{4}$ . The following tree diagram represents these events.

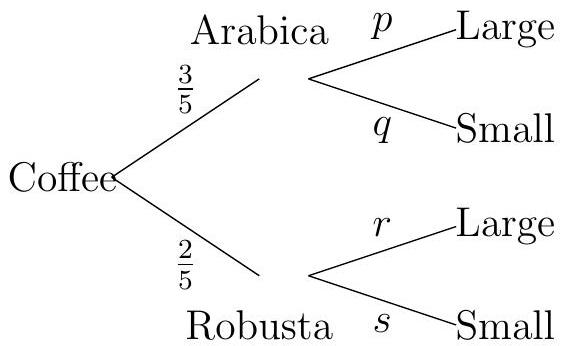
Complete the tree diagram by finding the values of $p, q, r$ , and $s$ .

[2]

Find the probability that a customer buys a large coffee.

[3]

Given that a customer buys a large coffee, find the probability they purchased Arabica.

[3]

Question 2

SLPaper 1

In a game show, a contestant chooses one of three doors. The probability that a prize is behind door A is $\frac{1}{4}$ , behind door B is $\frac{1}{3}$ , and behind door C is $\frac{5}{12}$ . After choosing a door, the contestant can either stay with their choice or switch to another door. If the contestant switches, the probability of winning is $\frac{7}{12}$ .

Calculate the probability that the contestant wins if they stay with their initial choice.

[3]

Determine whether the events "choosing door A" and "winning by switching" are independent.

[3]

Question 3

SLPaper 1

In a group of 60 students, 35 study French, 30 study Spanish, and 10 study both languages. Let $F$ represent the event "studies French" and $S$ represent the event "studies Spanish". The following Venn diagram shows these events, with $x, y$ , and $z$ representing numbers of students. $z$

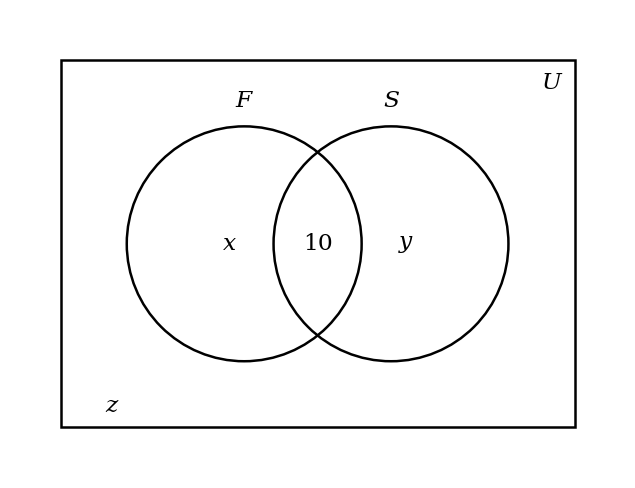
Find the values of $x, y$ , and $z$ .

[3]

Calculate the probability that a randomly selected student studies exactly one language.

[2]

Determine whether the events $F$ and $S$ are independent.

[3]

Question 4

SLPaper 1

A spinner is divided into four equal sectors labeled $\mathrm{A}, \mathrm{B}, \mathrm{C}$ , and D . The spinner is spun twice, and the outcomes are recorded. The probability of landing on each sector is $\frac{1}{4}$ .

Complete the following table to show the probabilities of all possible outcomes for two spins.

	A	B	C	D
A	$\frac{1}{16}$
B
C
D

[3]

Find the probability that the spinner lands on the same sector twice.

[2]

Find the probability that at least one spin lands on sector A.

[3]

Question 5

SLPaper 2

A medical test for a rare disease has a $99 \%$ accuracy rate for detecting the disease in infected individuals and a $97 \%$ accuracy rate for correctly identifying non-infected individuals. It is known that $2 \%$ of the population has the disease. The following tree diagram represents the test outcomes.

Complete the tree diagram by finding the values of $a, b, c$ , and $d$ .

[2]

Find the probability that a randomly selected individual tests positive.

[3]

Find the probability that an individual is infected given that they test positive.

[3]

Two individuals are tested independently. Find the probability that both test negative.

[3]

Among 500 tested individuals, estimate the expected number who are infected and test positive.

[2]

Determine whether the events "testing positive" and "being infected" are independent.

[3]

Question 6

SLPaper 2

A bag contains 6 red marbles and 4 blue marbles. Two marbles are drawn at random without replacement.

Complete the following tree diagram to show the probabilities for the two draws. [

[3]

Find the probability that both marbles are red.

[2]

Find the probability that the second marble is blue, given that the first marble is red. [3]

[3]

Question 7

SLPaper 2

On a given day, the probability that it rains in the morning is $\frac{2}{3}$ . If it rains in the morning, the probability that Sarah takes the bus to school is $\frac{3}{4}$ . If it does not rain in the morning, the probability that Sarah takes the bus is $\frac{1}{5}$ . The following tree diagram represents these events.

Complete the tree diagram by finding the values of $a, b, c$ , and $d$ .

[2]

Calculate the probability that Sarah takes the bus to school on a given day.

[3]

Question 8

SLPaper 1

Let $A$ and $B$ be two events

Let $P(A) = P(B) = 0.4$ and $P(A \cap B) = 0.2$ . Find $P(B|A)$ .

[2]

Find $P(A|B)$ .

[1]

Show that for any two events $A$ and $B$ where $P(A) = P(B)$ , the conditional probabilities $P(A|B)$ and $P(B|A)$ are equal.

[1]

Question 9

HLPaper 2

Occurrences $X$ and $Y$ are such that ${P}(X \cup Y) = 0.95$ , ${P}(X \cap Y) = 0.6$ and ${P}(X|Y) = 0.75$ .

Find ${\text{P}}(Y)$ .

[2]

Find $P(X)$ .

[2]

Hence show that occurrences $X'$ and $Y$ are independent.

[2]

Question 10

SLPaper 2

Occurrences X and Y are independent and P(X) = 3P(Y). Given that P(X ∪ Y) = 0.68, find P(Y).

Find P(Y).

[6]

SL 4.6—Combined, mutually exclusive, conditional, independence, prob diagrams Questionbank