- IB
- SL 4.5—Probability concepts, expected numbers
Practice SL 4.5—Probability concepts, expected numbers with authentic IB Mathematics Analysis and Approaches (AA) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like functions and equations, calculus, complex numbers, sequences and series, and probability and statistics. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
A bag contains 12 cards labeled with the numbers 1 to 12 . Three cards are drawn randomly without replacement.
Find the probability that the first card drawn is even-numbered.
Find the probability that the second card drawn is odd-numbered given that the first card was even-numbered.
Find the probability that all three cards drawn are even-numbered.
A store sells three types of drinks: cola (C), juice (J), and water (W). A survey of 80 customers shows that 45 buy cola, 40 buy juice, 30 buy water, 20 buy both cola and juice, 15 buy both cola and water, 10 buy both juice and water, and 5 buy all three.
Complete the Venn diagram for drink purchases.

Find the probability that a randomly chosen customer buys at least two types of drinks.
Find the expected number of customers buying only juice in a sample of 25 customers.
Let and be two events
Let and . Find .
Find .
Show that for any two events and where , the conditional probabilities and are equal.
Two fair 4-sided dice are rolled. Each die has faces numbered from 1 to 4.
List the sample space of all the outcomes of the two dice along with their sums.
Find the probability that the sum of the numbers on the two dice is greater than or equal to 6.
Find the probability that the sum of the numbers on the two dice is smaller than 6 through a different approach than the previous part.
If these dice rolls were repeated 10 times, what would be the probability to see the sum greater than or equal to 6 exactly 5 times.
A survey of 60 students at a school shows that 32 take biology (B), 28 take chemistry (C), and 15 take both subjects.
Complete the Venn diagram to represent the subject choices.
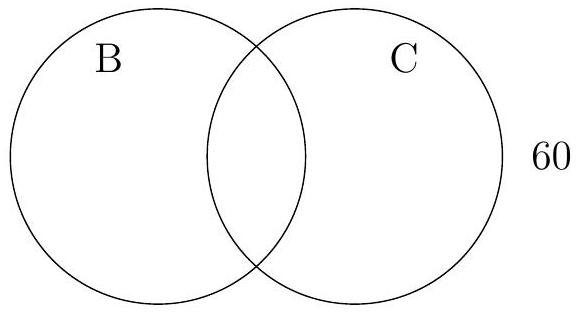
Find the number of students who take neither biology nor chemistry.
A student is chosen at random. Find the probability that the student takes chemistry given that they take biology.
Find the expected number of students taking only biology in a random sample of 20 students.
Two urns contain red (R) and blue (B) balls:
- Urn A: 5 R, 7 B (12 balls)
- Urn B: 4 R, 6 B (10 balls)
An experiment proceeds as follows (independently each time it is run).
- With probability (Procedure I): draw two balls without replacement from Urn A.
- With probability (Procedure II): transfer one ball chosen uniformly at random from Urn A to Urn B, then draw two balls without replacement from Urn B.
Let be the event “the two drawn balls are both red”.
Under Procedure I, find and .
Under Procedure II, find .
Find the overall probability .
Given that the two drawn balls are both red, find the posterior probability that Procedure II was used.
Under Procedure II, given that the two drawn balls are both blue, find the probability that the transferred ball was blue.
The experiment is performed twice independently. Find the probability that exactly one run results in both red.
Chloe and Selena play a game where each have four cards showing capital letters A, B, C and D.
Chloe lays her cards face up on the table in order A, B, C, D as shown in the following diagram.
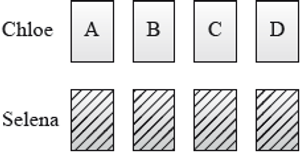
Selena shuffles her cards and lays them face down on the table. She then turns them over one by one to see if her card matches with Chloe’s card directly above.
Chloe wins if no matches occur; otherwise Selena wins.
Chloe and Selena repeat their game so that they play a total of 50 times.
Suppose the discrete random variable represents the number of times Chloe wins.
Show that the probability that Chloe wins the game is .
Determine the mean of .
Determine the variance of .
A school organizes a survey of 120 students participating in three clubs: literature (L), science (S), and drama (D). The following information is known:
- 50 students are in the literature club, 70 are in the science club, and 60 are in the drama club.
- 20 students are in both literature and science, 25 are in both literature and drama, and 35 are in both science and drama.
- 10 students are in all three clubs.
- 10 students are not in any of the clubs.
A game is played where a student is selected at random, and points are awarded based on club membership: 3 points for each club they are in, but if they are in no clubs, they lose 6 points. Let represent the points earned.
Draw a Venn diagram to represent the club memberships, labeling sets L, S, and D.
Find the probability that a randomly selected student is in exactly two clubs.
Construct the probability distribution table for .
Calculate the expected value of .
Determine whether membership in the literature and science clubs is independent.
Three cats and four dogs are seated randomly on a straight bench. Find the probability that the cats sit together and the dogs sit together.
Consider two events and that are mutually exclusive.
Given that , show that and are not mutually exclusive.