RevisionDojo

SL 2.4—Key features of graphs, intersections using technology - IB Questionbank | RevisionDojo

Practice SL 2.4—Key features of graphs, intersections using technology with authentic IB Mathematics Analysis and Approaches (AA) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like functions and equations, calculus, complex numbers, sequences and series, and probability and statistics. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.

Paper

Level

Question 1

SLPaper 1

The concentration of a chemical in a solution, in milligrams per liter ( $\mathrm{mg} / \mathrm{L}$ ), is modeled by the function $C(t)=C_{0} e^{-k t}$ , where $t$ is the time in hours after the chemical is added, and $C_{0}, k$ are positive constants.

The graph below shows the concentration over the first 8 hours.

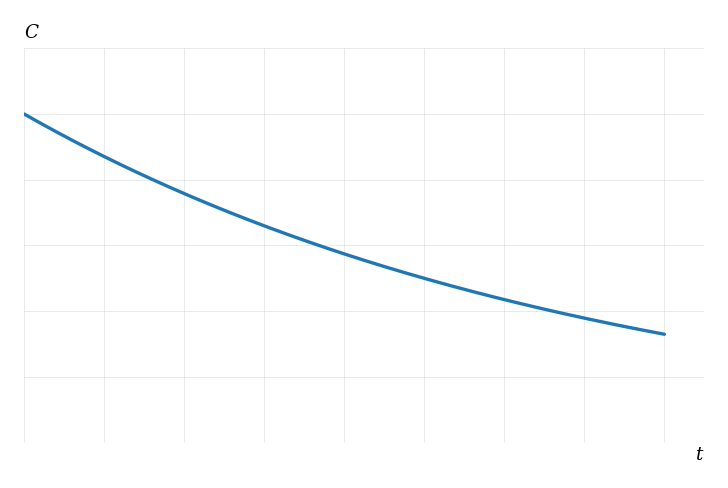
The initial concentration is $5 \mathrm{mg} / \mathrm{L}$ , and after 5 hours, the concentration is $2.5 \mathrm{mg} / \mathrm{L}$ . All concentrations are given correct to one decimal place.

Show that $C_{0}=5$ .

[1]

Find the value of $k$ , giving your answer in the form $\frac{1}{5} \ln a$ , where $a$ is a rational number.

[3]

Find the concentration when $t=3$ .

[2]

Question 2

SLPaper 2

A quadratic model $f(x)=ax^2+bx+c$ is fitted to three measured points $P(1,0.5+\ln 6)$ , $Q(3,1.5+\ln 9)$ , $R(6,\ln 5)$ .

Determine $a,b,c$ (numerically). Give your values correct to 3 significant figures.

[5]

Write $f(x)$ in vertex form $f(x)=a(x-h)^2+k$ . Hence state the vertex and the range of $f$ . Give $h,k$ to 3 d.p.

[4]

Let $g(x)=\ln(x+2)+1$ . Solve $f(x)=g(x)$ for $x\ge 0$ to 3 d.p., and justify the number of solutions.

[6]

Solve $f(x)\ge g(x)$ for $x\ge 0$ .

[3]

Question 3

SLPaper 2

Let $f(x)=e^{kx},\quad g(x)=\ln(x+9),\quad x>-9,\ k>0.$ It is given that $(f\circ g)(1)=7$ .

Determine $k$ correct to 3 significant figures.

[3]

Find the composites and their maximal domains.

[4]

Solve $(x+9)^k=\ln(9+e^{kx})$ for $x\ge0$ (3 d.p.) and justify uniqueness.

[7]

Find $(f\circ g)^{-1}(y)$ and state domain/range.

[4]

Question 4

SLPaper 2

A line through $A(-4,3)$ with gradient $m$ meets $C:\ y=x^2+8x$ at $P,Q$ . The distance $PQ=11$ .

Show the $x$ -coordinates satisfy $x^2+(8-m)x+(-4m-3)=0.$

[4]

State the condition on $m$ for two distinct intersections.

[2]

Show $(x_P-x_Q)^2=m^2+76$ .

[3]

Solve for $m$ using $PQ=11$ .

[4]

Question 5

SLPaper 2

A rational function has vertical asymptote $x=4$ and horizontal asymptote $y=1$ . It passes through $(0,-1)$ and $(5,9)$ .

Show $f(x)=1+\dfrac{k}{x-4}$ and determine $k$ . Hence express $f(x)=\dfrac{ax+b}{cx+d}$ with integers.

[4]

Determine domain, range, intercepts, asymptotes, and the sign of $f(x)-1$ on $(- \infty,4)$ , $(4,\infty)$ .

[5]

Solve $f(x)=g(x)$ to 3 d.p. and justify one solution in each of $(-1,4)$ and $(4,\infty)$ .

[6]

Describe the transformations from $y=1/x$ to $y=f(x)$ .

[2]

Question 6

SLPaper 2

A rational function has vertical asymptote $x=4$ and horizontal asymptote $y=7$ . It passes through the points $(0,5)$ and $(6,11)$ .

Show that the function can be written in the form $f(x)=7+\frac{k}{x-4}$ for some constant $k$ , and determine $k$ . Hence write $f(x)$ explicitly as $\dfrac{ax+b}{cx+d}$ with integer coefficients.

[4]

Determine all key features of $f$ : domain, range, intercepts, asymptotes, and the sign of $f(x)-7$ on $(- \infty,4)$ and $(4,\infty)$ .

[5]

Solve $f(x)=g(x)$ to three decimal places and justify exactly one solution in each of $(-1,4)$ and $(4,\infty)$ .

[6]

Describe transformations mapping $y=1/x$ to $y=f(x)$ .

[2]

Question 7

SLPaper 2

A quadratic model $f(x)=ax^2+bx+c$ is fitted to three measured points $P(1,1+\ln 2)$ , $Q(3,e)$ , $R(6,\ln 2)$ .

Determine $a,b,c$ (numerically). Give your values correct to 3 significant figures.

[5]

Write $f(x)$ in vertex form $f(x)=a(x-h)^2+k$ . Hence state the vertex and the range of $f$ . Give $h,k$ to 3 d.p.

[4]

Let $g(x)=\ln(x+2)+1$ . Solve $f(x)=g(x)$ for $x\ge 0$ to 3 d.p., and justify the number of solutions.

[6]

Solve $f(x)\ge g(x)$ for $x\ge 0$ .

[3]

Question 8

SLPaper 2

Let $f(x)=e^{kx},\quad g(x)=\ln(x+7),\quad x>-7,\ k>0.$ It is given that $(f\circ g)(0)=3$ .

Determine $k$ correct to 3 significant figures.

[3]

Find the composites and state maximal domains.

[4]

Solve $(x+7)^k=\ln(7+e^{kx})$ for $x\ge0$ (3 d.p.) and justify uniqueness.

[7]

Find $(f\circ g)^{-1}(y)$ and its domain/range.

[4]

Question 9

SLPaper 2

The basic function is $f(x)=\sqrt{x}$ for $x\ge 0$ . Define the transformed function $g(x)=3\sqrt{x-4}+1,\quad x\ge 4.$

Describe, step by step, the transformations that map $y=f(x)$ to $y=g(x)$ .

[4]

State the domain and range of $g$ .

[2]

Solve $3\sqrt{x-4}+1=x-2$ for $x\ge 4$ , giving your answers correct to 3 d.p.

[5]

Define $k(x)=|g(x)|,\ x\ge 4$ . Using technology, solve $k(x)=x-2$ for $4\le x\le 13$ . Give all solutions correct to 3 d.p.

[5]

Question 10

SLPaper 2

For a real parameter $p$ , consider the quadratic $q_p(x)=x^2-(p+2)x+(2p-5).$

Find all real values of $p$ for which $q_p$ has two distinct real roots and both roots are greater than $0$ .

[6]

Find the exact roots of $q(x)=0$ .

[3]

Solve $q(x)=g(x)$ for $x\ge0$ to three decimal places. Justify the number of solutions on $x\ge0$ .

[6]

Solve $q(x)\ge g(x)$ for $x\ge0$ (endpoints to 3 d.p.).

[3]

SL 2.4—Key features of graphs, intersections using technology Questionbank