Practice B.3 Gas laws with authentic IB Physics exam questions for both SL and HL students. This question bank mirrors Paper 1A, 1B, 2 structure, covering key topics like mechanics, thermodynamics, and waves. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
The graph shows the variation of pressure with volume for a fixed amount of gas. Two curves are shown:
- The dashed line represents gas behavior at temperature .
- The solid line represents the same gas at a higher temperature .
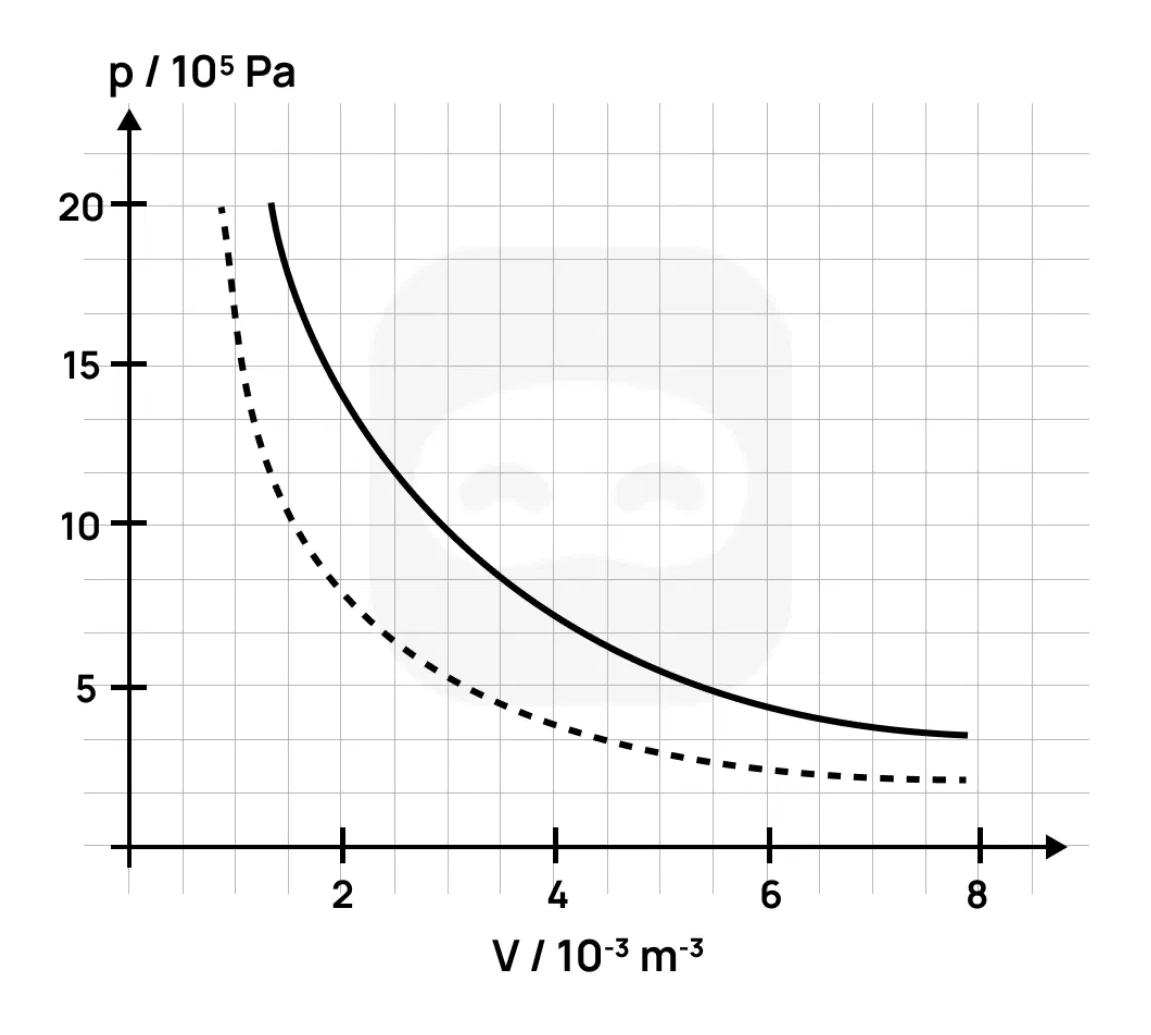
State the relationship between pressure and volume for a fixed mass of gas at constant temperature.
Using the graph, outline how pressure changes with increasing volume for both curves.
Explain how the graph indicates that the solid curve corresponds to a higher temperature.
Determine the pressure when the volume is for both curves.
A sealed container holds a fixed mass of gas at constant temperature. The volume of the gas is reduced from to .
State the gas law that applies to this situation.
If the initial pressure is , calculate the final pressure.
Explain why the pressure increases as the volume decreases.
A cylinder of height contains a fixed mass of ideal gas. A piston is used to compress the gas isothermally (at constant temperature ). The initial volume and pressure of the gas are and respectively. After compression, the piston is located at height , so the gas occupies only of its original volume.
Assume the cross-sectional area of the cylinder remains constant throughout the process.
State the ideal gas law.
Outline two assumptions of the ideal gas model.
State the ratio of the volumes of the gas before () and after () compression.
The temperature of the gas remains constant at . Using the ideal gas law, determine the ratio where is the pressure after compression.
Explain why, during this isothermal compression, work is done on the gas.
The gas is then heated at constant volume until its pressure reaches . Determine the final temperature in terms of the initial temperature .
A gas is trapped in a cylinder with a movable piston. The gas is slowly heated, and its volume is observed to increase while the pressure remains constant.
State the gas law that describes this behaviour.
If the initial volume is at , calculate the new volume when the temperature is increased to .
Explain the relationship between temperature and volume in this context.
The diagram shows a cyclic process for a fixed amount of an ideal gas undergoing four steps.
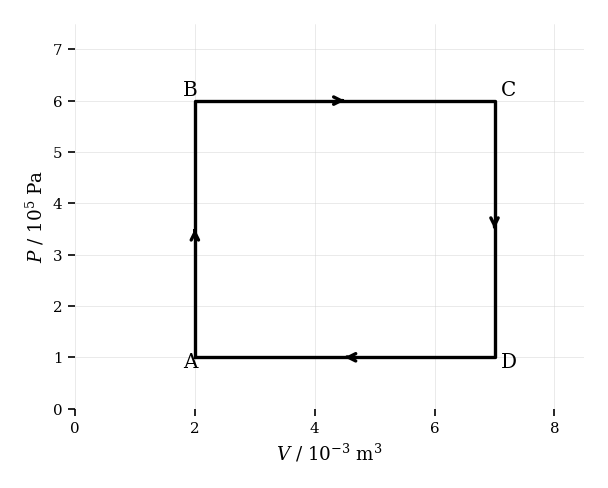
Describe the temperature changes along each segment of the cycle.
Calculate the work done by the gas during the segment .
Determine the net work done over the complete cycle.
Outline whether the gas does net positive or negative work over the full cycle, based on the diagram.
A sample of an ideal monatomic gas is at a pressure of and a volume of . The molar mass of the gas is .
Calculate the number of moles of gas in the sample.
Determine the temperature of the gas.
Calculate the total internal energy of the gas.
Explain why the internal energy of a monatomic ideal gas is entirely kinetic.
Two rigid containers are connected by a closed valve.
- The left container has volume and contains gas at pressure and temperature .
- The right container has volume and contains gas at pressure and the same temperature .
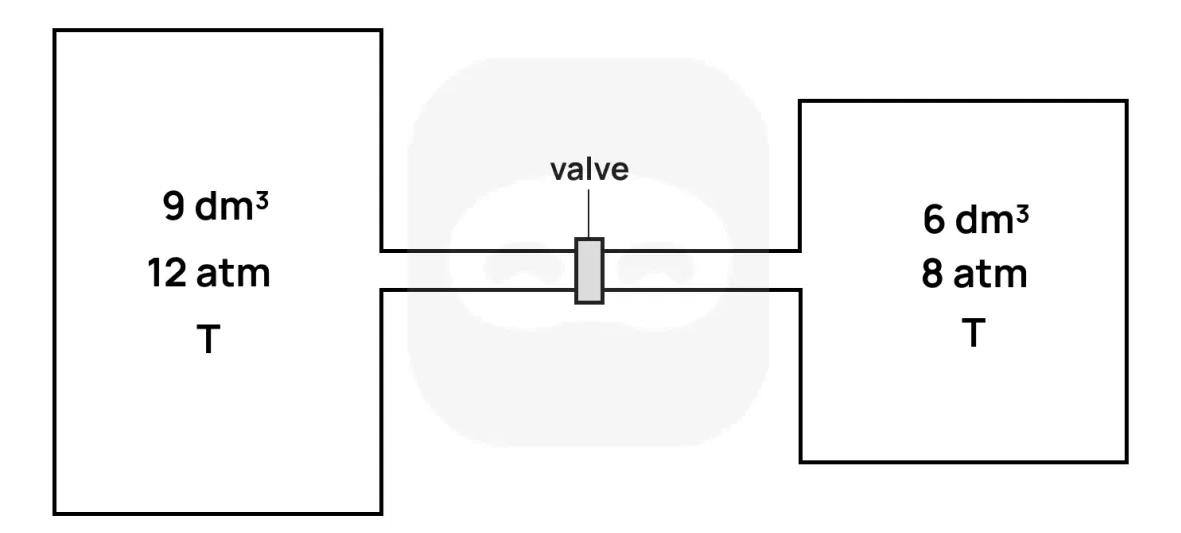
The valve is then opened and the gases are allowed to mix and reach equilibrium. Assume temperature remains constant and the gases are ideal and non-reactive.
State the ideal gas law.
Determine an expression for the number of moles in each container before the valve is opened, in terms of and .
Determine an expression for the total number of moles in the system.
Calculate the final equilibrium pressure of the system after the valve is opened.
Suggest why temperature must remain constant for this pressure calculation to be valid.
Container contains 1.0 mol of an ideal gas. Container contains 2.0 mol of the ideal gas. has four times the volume of . The pressure in is twice that in .
What is ?
A gas storage tank of fixed volume V contains N molecules of an ideal gas at temperature T. The pressure at kelvin temperature T is 20 MPa. molecules are removed and the temperature changed to 2T. What is the new pressure of the gas?
A balloon contains an ideal monatomic gas at a temperature of and a pressure of . The volume of the balloon is . The molar mass of the gas is .
Calculate the number of moles of gas in the balloon.
Determine the root-mean-square (rms) speed of the gas molecules.
Calculate the total internal energy of the gas.
Explain the relationship between the rms speed and the temperature of the gas.