Practice C.4 Standing waves and resonance with authentic IB Physics exam questions for both SL and HL students. This question bank mirrors Paper 1A, 1B, 2 structure, covering key topics like mechanics, thermodynamics, and waves. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
The diagram shows a standing wave formed on a string with both ends fixed. Points A and B are marked. Point B lies at a point of zero displacement, and point A lies at a point of maximum displacement.
Identify whether points A and B are nodes or antinodes.
State the condition for the formation of a standing wave on a string.
Determine the wavelength of the wave if the length of the string is .
Outline how this standing wave is produced by two traveling waves.
The diagram shows a vertical tube partially submerged in water. A tuning fork is held above the open end, and the air column length above the water can be adjusted. The setup is used to investigate the resonance of sound waves in a tube closed at one end (bottom) and open at the top.
State the condition for resonance to occur in the air column.
Outline how the length relates to the wavelength of the sound at the first harmonic.
A tuning fork of frequency produces the first harmonic when . Calculate the speed of sound in air.
Outline why resonance does not occur for all values of .
The diagram shows a wave moving along a string from left to right (solid line), followed by its reflection (dashed line) from the right-hand boundary. The two waves are of the same amplitude and frequency. This setup illustrates the formation of a standing wave.
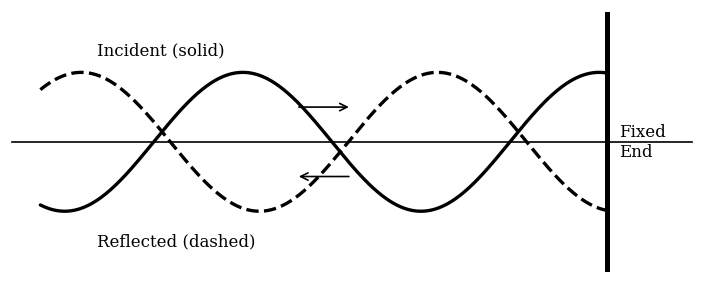
State one feature of the reflected wave that indicates it is undergoing inversion at the boundary.
Identify the type of wave interference occurring where the two waves overlap.
Outline the condition required for a standing wave to form on the string.
The diagram shows a standing wave in a tube that is closed at both ends. A loudspeaker at one of the closed ends generates sound waves, as shown in the diagram below. The wave shown represents the displacement of air particles in the tube.
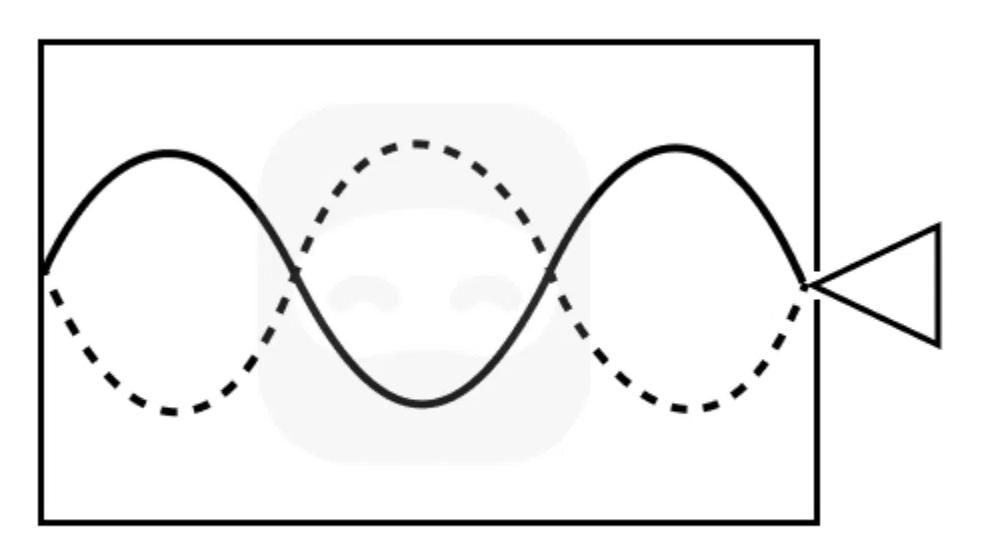
State the boundary conditions for displacement at the closed ends of the tube.
Identify the harmonic shown in the diagram.
Determine the wavelength of the sound wave if the length of the tube is .
Outline how the standing wave is formed in this air column.
The diagram shows a standing wave on a string fixed at both ends. Three points, A, B, and C, are marked on the wave. The wave is oscillating in its third harmonic mode.
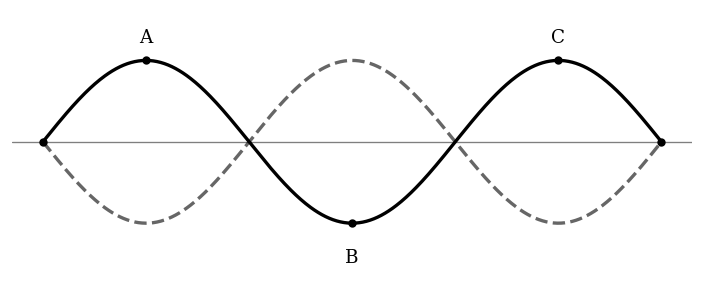
Identify the type of point (node or antinode) at positions A, B, and C.
State the number of wavelengths that fit along the string.
State the phase relationship between the motion of points A and C.
Outline how the wave shown is formed by the superposition of two travelling waves.
A student wants to determine the speed of electromagnetic waves inside a microwave oven. They remove the rotating plate and place a flat slab of chocolate on the base of the oven. After heating for a few seconds, the chocolate begins to melt at fixed points. The frequency of the microwave is printed on the back of the oven: .
Explain how standing waves are formed inside the microwave oven and why they result in specific points of heating.
Describe how the student could use the melted chocolate to determine the wavelength of the microwave radiation.
The student observes that the distance between melted regions is . Calculate the speed of the microwave radiation in air.
State one assumption and one source of uncertainty in this experiment.
Explain why this experiment does not work with the rotating plate.
In a second attempt, the student forgets to remove the rotating platform. After running the microwave, the entire chocolate slab melts uniformly. Explain why this occurred and why it prevents determining the speed of microwaves.
Which of the following best explains why the sound intensity sharply increases when a pipe reaches its resonant length for a particular frequency?
A string of length is fixed at both ends and supports a standing wave pattern with three antinodes when under tension. The wave speed on the string is .
State the harmonic number of this standing wave.
Calculate the wavelength of the wave on the string.
Calculate the frequency of the wave.
Sketch the standing wave pattern on the string, showing all nodes and antinodes.
The tension in the string is increased. Explain the effect this has on the frequency of the standing wave, assuming the harmonic number stays the same.
A tube is closed at one end and open at the other.
Draw the fundamental mode of the standing wave in the tube.
State the position of the node and antinode.
State the length of the tube in terms of the wavelength.
A string of length is fixed at both ends and supports standing waves. The wave speed is .
Derive an expression for the wavelength of the harmonic on the string.
In a pipe that is closed at one end and open at the other, only certain harmonics are observed. Explain why some harmonics are missing in such a tube.
Calculate the frequency of the fourth harmonic for the string.
Sketch the standing wave pattern corresponding to the second and fourth harmonic on the string.
Compare the harmonic series for a string fixed at both ends and a pipe closed at one end. Sketch for (d): Second harmonic: 1 full wavelength → 3 nodes, 2 antinodes Fourth harmonic: 2 full wavelengths → 5 nodes, 4 antinodes