Radian Measure of Angles
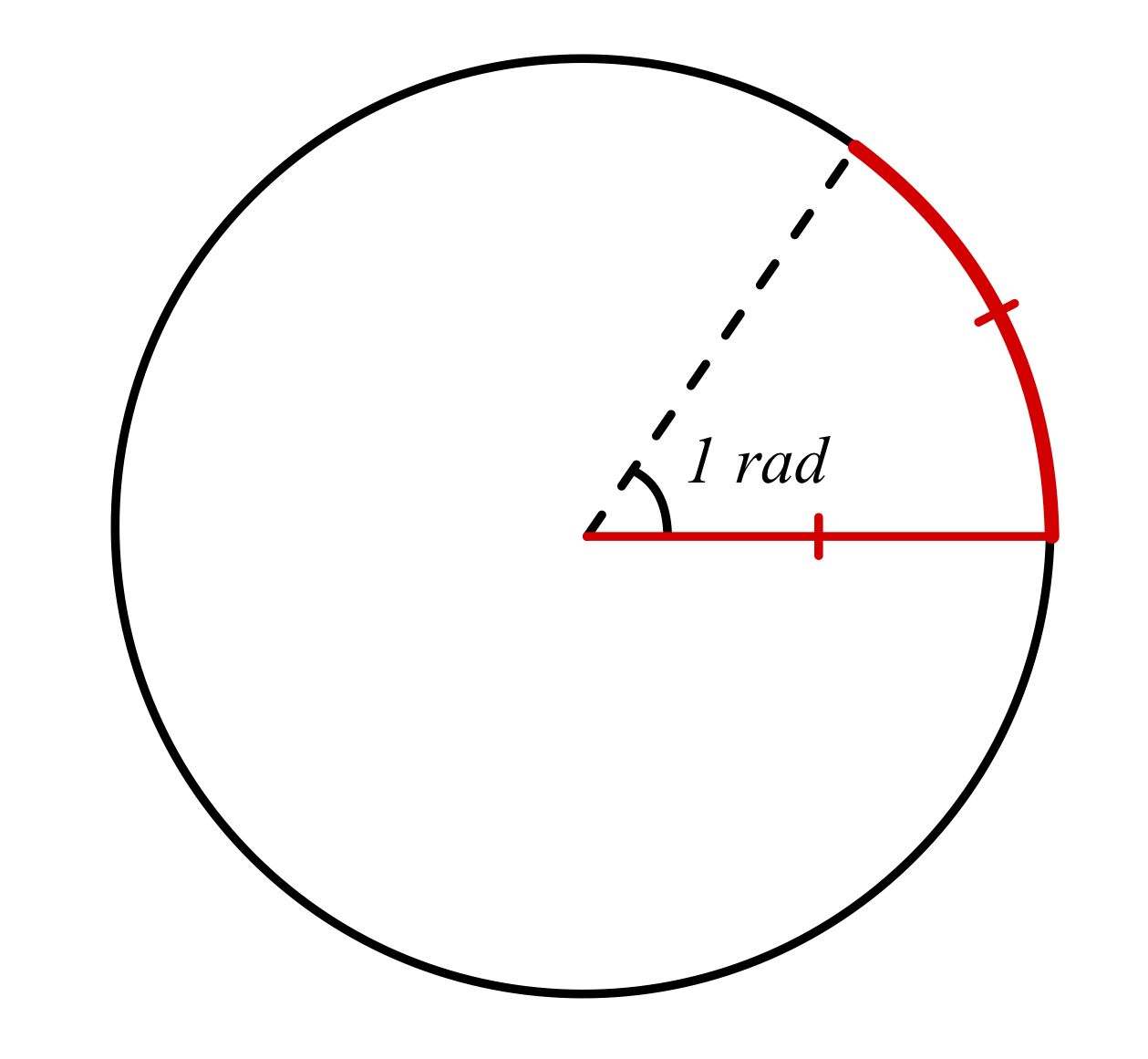
Radian measure is a way of describing angles using the radius of a circle. One radian is defined as the angle subtended at the center of a circle by an arc length equal to the radius of the circle.
Note$1\ rad$ is approximately equal to $57.3°$.
NoteThe full angle around a circle is 2π radians, which is equivalent to 360°.
The formula for converting between degrees and radians is:
$\text{angle in radians} = \frac{\text{angle in degrees} \times \pi}{180°}$
$\text{angle in degrees} = \frac{\text{angle in radians} \times 180°}{\pi}$
ExampleConvert 45° to radians: $45° \times \frac{\pi}{180°} = \frac{\pi}{4}$ radians
Convert $\frac{2\pi}{3}$ radians to degrees: $\frac{2\pi}{3} \times \frac{180°}{\pi} = 120°$
TipMemorize common angle conversions like 30° = $\frac{\pi}{6}$, 45° = $\frac{\pi}{4}$, and 60° = $\frac{\pi}{3}$.
Length of an Arc
The length of an arc is a portion of the circumference of a circle. The portion of the circumference an arc takes up is $\frac{\theta}{2\pi}$, where $\theta$ is the angle subtended by the arc in radians. This should (hopefully) be intuitive. Therefore,
$\text{Arc length} = \frac{\theta}{2\pi}2\pi r = r\theta$
Where:
- $r$ is the radius of the circle
- $\theta$ is the angle subtended by the arc in radians
Calculate the length of an arc that subtends an angle of $\frac{\pi}{3}$ radians in a circle with radius 5 cm.
$\text{Arc length} = r\theta = 5 \times \frac{\pi}{3} = \frac{5\pi}{3}$ cm ≈ 5.24 cm
Common MistakeRemember to always use radians for $\theta$ in this formula. If given an angle in degrees, convert it to radians first.
Area of a Sector
A sector is a region of a circle enclosed by two radii and an arc. The proportion of the area a sector takes up is also $\frac{\theta}{2\pi}$, where $\theta$ is the angle subtended by the sector in radians. Thus,