Trigonometric Ratios in Right-Angled Triangles
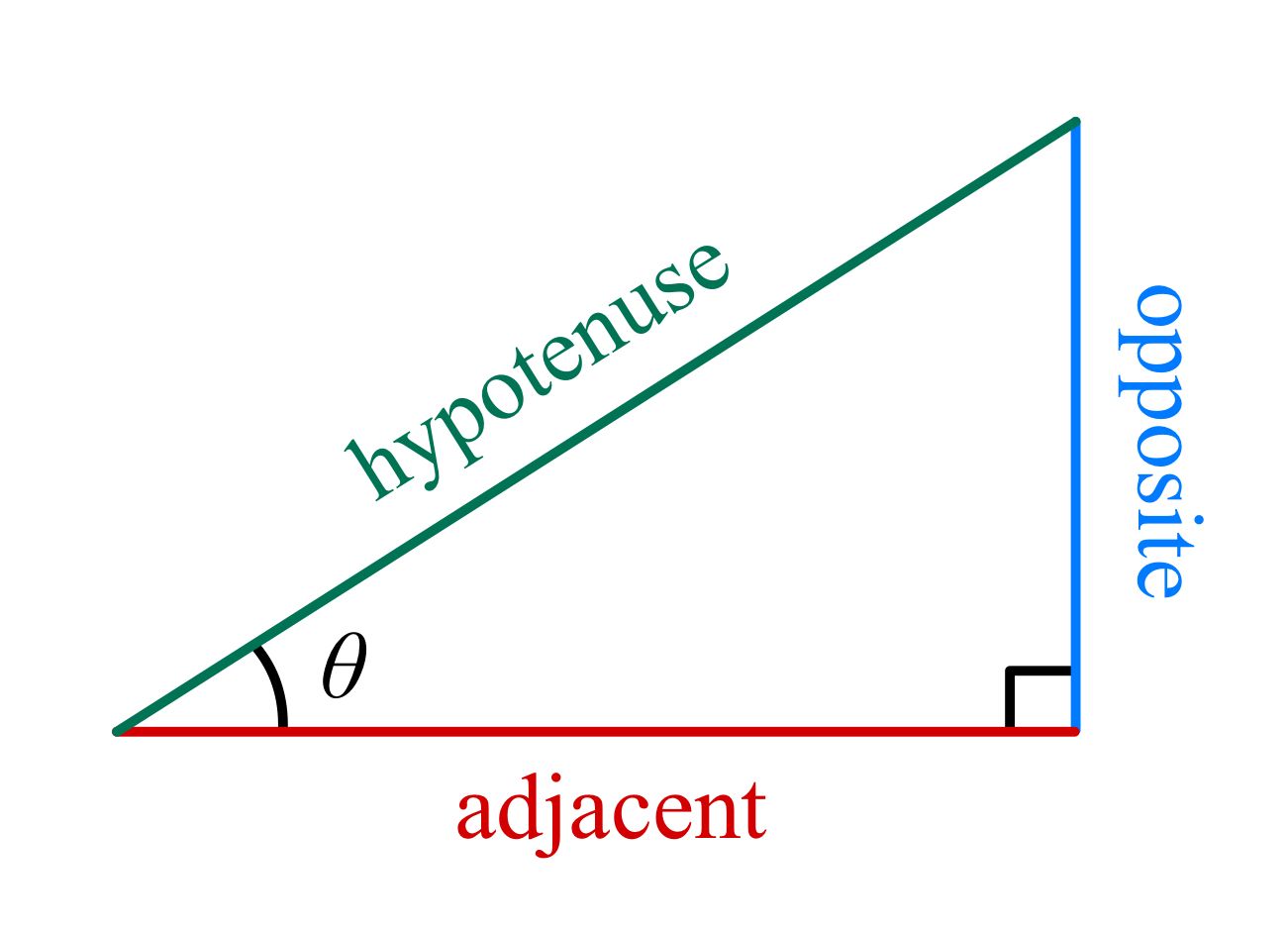
Trigonometric ratios are ratios of sides of right-angled triangles, dependent on the angles in the triangle. To make use of these, we label the sides on a triangle with relation to an angle $\theta$:
- The hypotenuse is the longest side of the right-angled triangle, opposite the right angle.
- The opposite side to an angle $\theta$ is the only side the angle does not touch.
- The adjacent side to an angle $\theta$ is the only non-hypotenuse side the angle touches.
The three primary ratios are sine, cosine, and tangent.
For a right-angled triangle with an angle θ:
- $\sin θ = \frac{\text{opposite}}{\text{hypotenuse}}$
- $\cos θ = \frac{\text{adjacent}}{\text{hypotenuse}}$
- $\tan θ = \frac{\text{opposite}}{\text{adjacent}}$
Additionally, we can express $\tan\theta$ in terms of $\sin\theta$ and $\cos\theta$:
$$\tan\theta = \frac{\text{opposite}}{\text{adjacent}}$$
$$\tan\theta = \frac{\frac{\text{opposite}}{\text{hypotenuse}}}{\frac{\text{adjacent}}{\text{hypotenuse}}}$$
$$\tan\theta = \frac{\sin\theta}{\cos\theta}$$
ExampleConsider a right-angled triangle with hypotenuse 10 cm and an angle of 30°. To find the length of the side opposite to 30°:
$\sin 30° = \frac{\text{opposite}}{10}$
$\text{opposite} = 10 \sin 30° = 10 \times 0.5 = 5$ cm
TipRemember the mnemonic SOH-CAH-TOA to recall these ratios easily:
- Sine = Opposite / Hypotenuse
- Cosine = Adjacent / Hypotenuse
- Tangent = Opposite / Adjacent
The Sine Rule
The sine rule is used in non-right angled triangles when we know:
- Two angles and one side, or
- Two sides and the angle opposite one of them
The sine rule states: