Practice SL 1.2—Sequences and Sigma Notation with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
It is known that the number of fish in a certain pond will decrease by each year unless some new fish are added. At the end of each year, 250 new fish are added to the pond.
At the start of 2018, there are 2500 fish in the pond.
Show that there will be approximately 2645 fish in the pond at the start of 2020.
Find the approximate number of fish in the pond at the start of 2042.
Scott purchases food for his dog in large bags and feeds the dog the same amount of dog food each day. The amount of dog food left in the bag at the end of each day can be modelled by an arithmetic sequence. On a particular day, Scott opened a new bag of dog food and fed his dog. By the end of the third day there were 115.5 cups of dog food remaining in the bag and at the end of the eighth day there were 108 cups of dog food remaining in the bag.
Find the number of cups of dog food fed to the dog per day.
Find the number of cups of dog food remaining in the bag at the end of the first day.
Calculate the number of days that Scott can feed his dog with one bag of food.
In 2021, Scott spent $625 on dog food. Scott expects that the amount he spends on dog food will increase at an annual rate of 6.4%. Determine the amount that Scott expects to spend on dog food in 2025. Round your answer to the nearest dollar.
Calculate the value of .
Describe what the value in part (i) represents in this context.
Comment on the appropriateness of modeling this scenario with a geometric sequence.
A software company is tracking the number of downloads of its app, where the downloads at month are defined by the sequence .
Write down the first three terms of the download sequence.
Find , the number of downloads at month 10.
Calculate , the total downloads over the first three months.
Rosa joins a club to prepare to run a marathon. During the first training session Rosa runs a distance of 3000 metres. Each training session she increases the distance she runs by 400 metres.
A marathon is 42.195 kilometres.
In the th training session Rosa will run further than a marathon for the first time.
Carlos joins the club to lose weight. He runs 7500 metres during the first month. The distance he runs increases by 20% each month.
Write down the distance Rosa runs in the third training session.
Find the value of .
Calculate the total distance, in kilometres, Rosa runs in the first 50 training sessions.
Calculate the total distance Carlos runs in the first year.
Find the distance Carlos runs in the fifth month of training.
Write down the distance Rosa runs in the th training session.
In a chemistry experiment, several quantities are measured, and their values are expressed in different forms. Understanding these values is crucial for accurate calculations. Let , , , and .
Identify the value written in the form where and .
Write down the smallest value among , , , and .
Calculate .
Express your answer from part 3 in the form where and .
A student is building a robot that is coded to take a certain number of steps. The first day it takes 1 step, the second day it takes 2 steps, the third day it takes 3 steps, and so on. Hence on the th day it takes steps.
Find the minimum number of days required for the total number of steps taken in all days to exceed 2023.
A pyramid of stacked cubes is being built for a mathematics exhibition to promote STEM education. The first level has 10 cubes, the second level has 12 cubes, and each additional level contains 2 more cubes than the previous level. The organisers have 1500 cubes available.
Find the number of cubes in the 10th level.
Derive the formula for the total number of cubes in the first levels.
Calculate the total number of cubes in the pyramid if it has 30 levels.
Determine the maximum number of complete levels that can be built with 1500 cubes.
If each cube has a side length of 0.4 m, calculate the total volume of the pyramid when the maximum levels are built.
In scientific research, measurements are often rounded to a certain number of significant figures. Understanding the range of possible values based on these figures is important for data analysis.
The value of is 34500, correct to 3 significant figures. State the range of possible values for .
The value of is 0.0301, correct to 3 significant figures. State the range of possible values for .
Two numbers, and , are rounded to the nearest unit. Find the smallest possible value and largest possible value of their addition where and .
A research study is analyzing the growth of a plant species, where the growth at month is defined by the sequence .
Write down the first three terms of the growth sequence.
Find , the growth at month 10.
Calculate , the total growth over the first three months.
In mathematics, numbers can belong to different sets: natural numbers (), integers (), rational numbers (), and real numbers (). A Venn diagram shows these sets, with each set nested within as follows: .
Given the numbers , , , , , and , place each in the appropriate region of the Venn diagram for and .
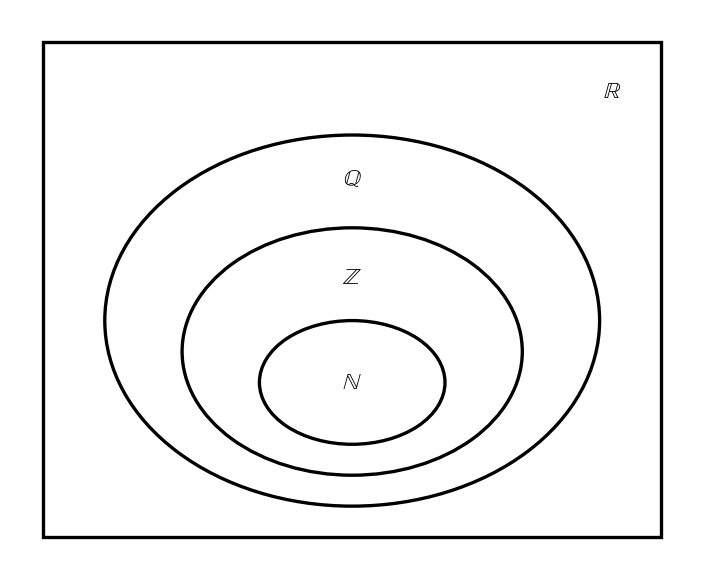
Identify and place each number in the correct set(s) based on its properties. Explain your reasoning briefly for each placement.
Practice SL 1.2—Sequences and Sigma Notation with authentic IB Mathematics Applications & Interpretation (AI) exam questions for both SL and HL students. This question bank mirrors Paper 1, 2, 3 structure, covering key topics like core principles, advanced applications, and practical problem-solving. Get instant solutions, detailed explanations, and build exam confidence with questions in the style of IB examiners.
It is known that the number of fish in a certain pond will decrease by each year unless some new fish are added. At the end of each year, 250 new fish are added to the pond.
At the start of 2018, there are 2500 fish in the pond.
Show that there will be approximately 2645 fish in the pond at the start of 2020.
Find the approximate number of fish in the pond at the start of 2042.
Scott purchases food for his dog in large bags and feeds the dog the same amount of dog food each day. The amount of dog food left in the bag at the end of each day can be modelled by an arithmetic sequence. On a particular day, Scott opened a new bag of dog food and fed his dog. By the end of the third day there were 115.5 cups of dog food remaining in the bag and at the end of the eighth day there were 108 cups of dog food remaining in the bag.
Find the number of cups of dog food fed to the dog per day.
Find the number of cups of dog food remaining in the bag at the end of the first day.
Calculate the number of days that Scott can feed his dog with one bag of food.
In 2021, Scott spent $625 on dog food. Scott expects that the amount he spends on dog food will increase at an annual rate of 6.4%. Determine the amount that Scott expects to spend on dog food in 2025. Round your answer to the nearest dollar.
Calculate the value of .
Describe what the value in part (i) represents in this context.
Comment on the appropriateness of modeling this scenario with a geometric sequence.
A software company is tracking the number of downloads of its app, where the downloads at month are defined by the sequence .
Write down the first three terms of the download sequence.
Find , the number of downloads at month 10.
Calculate , the total downloads over the first three months.
Rosa joins a club to prepare to run a marathon. During the first training session Rosa runs a distance of 3000 metres. Each training session she increases the distance she runs by 400 metres.
A marathon is 42.195 kilometres.
In the th training session Rosa will run further than a marathon for the first time.
Carlos joins the club to lose weight. He runs 7500 metres during the first month. The distance he runs increases by 20% each month.
Write down the distance Rosa runs in the third training session.
Find the value of .
Calculate the total distance, in kilometres, Rosa runs in the first 50 training sessions.
Calculate the total distance Carlos runs in the first year.
Find the distance Carlos runs in the fifth month of training.
Write down the distance Rosa runs in the th training session.
In a chemistry experiment, several quantities are measured, and their values are expressed in different forms. Understanding these values is crucial for accurate calculations. Let , , , and .
Identify the value written in the form where and .
Write down the smallest value among , , , and .
Calculate .
Express your answer from part 3 in the form where and .
A student is building a robot that is coded to take a certain number of steps. The first day it takes 1 step, the second day it takes 2 steps, the third day it takes 3 steps, and so on. Hence on the th day it takes steps.
Find the minimum number of days required for the total number of steps taken in all days to exceed 2023.
A pyramid of stacked cubes is being built for a mathematics exhibition to promote STEM education. The first level has 10 cubes, the second level has 12 cubes, and each additional level contains 2 more cubes than the previous level. The organisers have 1500 cubes available.
Find the number of cubes in the 10th level.
Derive the formula for the total number of cubes in the first levels.
Calculate the total number of cubes in the pyramid if it has 30 levels.
Determine the maximum number of complete levels that can be built with 1500 cubes.
If each cube has a side length of 0.4 m, calculate the total volume of the pyramid when the maximum levels are built.
In scientific research, measurements are often rounded to a certain number of significant figures. Understanding the range of possible values based on these figures is important for data analysis.
The value of is 34500, correct to 3 significant figures. State the range of possible values for .
The value of is 0.0301, correct to 3 significant figures. State the range of possible values for .
Two numbers, and , are rounded to the nearest unit. Find the smallest possible value and largest possible value of their addition where and .
A research study is analyzing the growth of a plant species, where the growth at month is defined by the sequence .
Write down the first three terms of the growth sequence.
Find , the growth at month 10.
Calculate , the total growth over the first three months.
In mathematics, numbers can belong to different sets: natural numbers (), integers (), rational numbers (), and real numbers (). A Venn diagram shows these sets, with each set nested within as follows: .
Given the numbers , , , , , and , place each in the appropriate region of the Venn diagram for and .

Identify and place each number in the correct set(s) based on its properties. Explain your reasoning briefly for each placement.