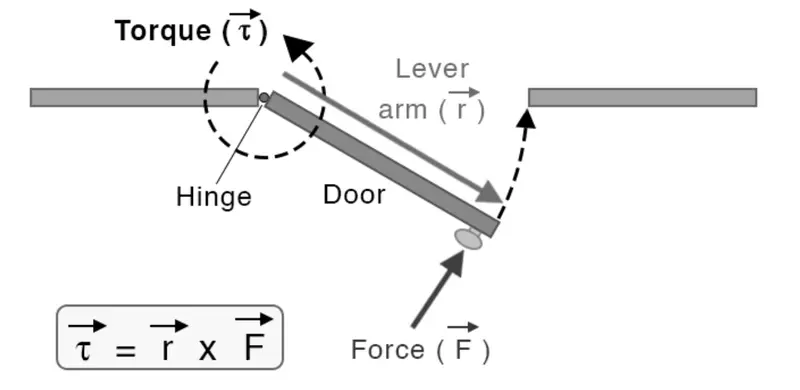
## Torque and Its Role in Rotation [block_0] 1. When you push a door near its **hinges**, it **barely **moves. 2. But if you push at the **edge**, it swings open **easily**. > This difference is due to **torque**, the rotational equivalent of force. ### What is Torque? [block_2] **Torque **is the rotational equivalent of force. It measures the ability of a force to cause an object to rotate. It depends on three factors: 1. **Magnitude of the Force **($F$) 2. **Distance from the Axis **($r$): This is the **lever arm**, the perpendicular distance from the axis to the line of action of the force. 3. **Angle**($\theta$): The angle between the force and the lever arm. The formula for **torque** ($\tau$) is: $$ \tau = Fr\sin\theta $$ [{"_key":"block_11","_type":"block","asset":null,"children":[{"_key":"7a3dbc8e458c","_type":"span","markDefs":[],"marks":["strong"],"text":"Units"},{"_key":"6b28b3410e16","_type":"span","markDefs":[],"marks":[],"text":": Torque is measured in "},{"_key":"9c83230e7c41","_type":"span","markDefs":[],"marks":["strong"],"text":"newton-meters (Nm)"},{"_key":"84b71af97503","_type":"span","markDefs":[],"marks":[],"text":". "}],"level":1,"listItem":"bullet","markDefs":[],"style":"normal"},{"_key":"9c6424791b34","_type":"block","asset":null,"children":[{"_key":"4d33e05bcb0e","_type":"span","markDefs":[],"marks":[],"text":"Although this is dimensionally equivalent to a joule, torque is"},{"_key":"527b47ae4fdc","_type":"span","markDefs":[],"marks":["strong"],"text":" never expressed in joules"},{"_key":"6f7f87fa823b","_type":"span","markDefs":[],"marks":[],"text":" because it is "},{"_key":"b508cc529e82","_type":"span","markDefs":[],"marks":["strong"],"text":"not "},{"_key":"2133c685c56b","_type":"span","markDefs":[],"marks":[],"text":"a form of "},{"_key":"e4639712ea6b","_type":"span","markDefs":[],"marks":["strong"],"text":"energy"},{"_key":"f9df43fe288b","_type":"span","markDefs":[],"marks":[],"text":"."}],"level":1,"listItem":"bullet","markDefs":[],"style":"normal"}] ![](https://cdn.sanity.io/images/w7j7fz60/production/011cab6abf75111157fddaf61fdfa534fa41e5c7-800x390.png) ### How Torque Works [block_12] 1. **Maximum Torque**: 1. Occurs when the force is **perpendicular **to the lever arm ($\theta = 90^\circ$), making $\sin\theta = 1$. 2. In this case, $\tau = Fr$. 2. **Zero Torque**: 1. If the force acts **along the line** of the lever arm ($\theta = 0^\circ$ or $180^\circ$), then $\sin\theta = 0$, and the torque is zero. [{"_key":"block_17","_type":"block","asset":null,"children":[{"_key":"5b2a8f535fc2","_type":"span","markDefs":[],"marks":[],"text":"Consider a wrench turning a bolt. "}],"level":1,"listItem":"bullet","markDefs":[],"style":"normal"},{"_key":"b54a506f7b3d","_type":"block","asset":null,"children":[{"_key":"8c496110ef95","_type":"span","markDefs":[],"marks":[],"text":"Applying a force of 50 N at a distance of 0.3 m from the bolt, perpendicular to the wrench, the torque is: $$\n\\tau = 50 \\, \\text{N} \\times 0.3 \\, \\text{m} \\times \\sin 90^\\circ = 15 \\, \\text{Nm}\n$$"}],"level":1,"listItem":"bullet","markDefs":[],"style":"normal"}] [{"_key":"block_21","_type":"block","asset":null,"children":[{"_key":"f471b0ad69fb","_type":"span","markDefs":[],"marks":[],"text":"To maximize torque, apply the force "},{"_key":"44b798d4b818","_type":"span","markDefs":[],"marks":["strong"],"text":"as far from the axis as possible"},{"_key":"12ff4f71d914","_type":"span","markDefs":[],"marks":[],"text":" and perpendicular to the lever arm."}],"markDefs":[],"style":"normal"}] ## Equilibrium Conditions: Translational and Rotational [block_22] For an object to be in **equilibrium**, it must satisfy two conditions: 1. **Translational Equilibrium**: The **net force **acting on the object is **zero**. 2. **Rotational Equilibrium**: The **net torque** acting on the object is **zero**. ### Translational Equilibrium [block_27] An object is in **translational equilibrium** when the sum of all the external forces acting on the object equals zero. > In other words, the object remains at rest or moves with constant velocity. Mathematically, this is expressed as: $$ \sum \vec{F} = 0 $$ ### Rotational Equilibrium [block_30] **Rotational equilibrium** is defined as the state of movement where angular acceleration is zero: total torque is zero. > In other words, in rotational equilibrium, the object does not rotate or rotates at a constant angular velocity. This is expressed as: $$ \sum \tau = 0 $$ [{"_key":"block_39","_type":"block","asset":null,"children":[{"_key":"ktJcs52erdY1dZ2NmDLfP0","_type":"span","markDefs":[],"marks":[],"text":"When solving equilibrium problems, choose "},{"_key":"fef3df171e3e","_type":"span","markDefs":[],"marks":["strong"],"text":"an axis of rotation"},{"_key":"c024c608d51e","_type":"span","markDefs":[],"marks":[],"text":" that simplifies calculations by "},{"_key":"16d7bef7a2a2","_type":"span","markDefs":[],"marks":["strong"],"text":"eliminating torques"},{"_key":"15556ea20c22","_type":"span","markDefs":[],"marks":[],"text":" from forces passing through the axis."}],"markDefs":[],"style":"normal"}] Consider a seesaw with a child weighing 300 N sitting 1.5 m from the pivot. To balance the seesaw, another child weighing 200 N must sit on the opposite side. How far should the second child sit? * **Calculate Torque for the First Child**:$$ \tau_1 = 300 \, \text{N} \times 1.5 \, \text{m} = 450 \, \text{Nm} $$ * **Set Torques Equal for Equilibrium**:$$ \tau_2 = 200 \, \text{N} \times d = 450 \, \text{Nm} $$ * **Solve for $d$**:$$ d = \frac{450 \, \text{Nm}}{200 \, \text{N}} = 2.25 \, \text{m} $$ * The second child should sit 2.25 m from the pivot. ![](https://cdn.sanity.io/images/w7j7fz60/production/fb44a75e8d7e390e2649bf51f046cb6285d06dd1-638x496.png) ## Rotational Kinematics: Angular Displacement, Velocity, and Acceleration [block_40] Rotational motion is described using angular quantities, analogous to linear motion. ### Angular Displacement ($\theta$) [block_42] **Angular displacement **is the angle through which an object moves on a circular path. It is measured in **radians**. [{"_key":"block_45","_type":"block","asset":null,"children":[{"_key":"ktJcs52erdY1dZ2NmDLfRP","_type":"span","markDefs":[],"marks":["strong"],"text":"1 radian"},{"_key":"918a6daaec69","_type":"span","markDefs":[],"marks":[],"text":" is the angle subtended by an arc equal in length to the radius of the circle."}],"markDefs":[],"style":"normal"}] ### Angular Velocity ($\omega$) [block_46] **Angular velocity **($\omega$) is the rate of change of angular displacement. It is measured in **radians per second** (rad/s). It is defined as: $$ \omega = \frac{\Delta \theta}{\Delta t} $$ [{"_key":"e2b1ce540679","_type":"block","asset":null,"children":[{"_key":"bf1ca5717b09","_type":"span","markDefs":[],"marks":[],"text":"The unit of angular velocity is "},{"_key":"3d95d2a8032d","_type":"span","markDefs":[],"marks":["strong"],"text":"radians per second ($\\text{rad s}^{-1}$)"},{"_key":"44a1db4e8779","_type":"span","markDefs":[],"marks":[],"text":"."}],"markDefs":[],"style":"normal"}] ### Angular Acceleration ($\alpha$) [block_50] **Angular acceleration **is the rate of change of angular velocity. It is defined as: $$ \alpha = \frac{\Delta \omega}{\Delta t} $$ [{"_key":"43e531df9071","_type":"block","asset":null,"children":[{"_key":"4fcf7b1a5896","_type":"span","markDefs":[],"marks":[],"text":"The unit of angular acceleration is "},{"_key":"aa4ed612310e","_type":"span","markDefs":[],"marks":["strong"],"text":"radians per second squared ($\\text{rad s}^{-2}$)"},{"_key":"566c5a68d2a1","_type":"span","markDefs":[],"marks":[],"text":"."}],"markDefs":[],"style":"normal"}] [{"_key":"block_55","_type":"block","asset":null,"children":[{"_key":"ip9ZSUgFyzGIsQgTfx596O","_type":"span","markDefs":[],"marks":[],"text":"Think of angular quantities as the rotational counterparts to linear quantities:"}],"markDefs":[],"style":"normal"},{"_key":"block_56","_type":"block","asset":null,"children":[{"_key":"ip9ZSUgFyzGIsQgTfx5986","_type":"span","markDefs":[],"marks":["strong"],"text":"Position"},{"_key":"ip9ZSUgFyzGIsQgTfx599o","_type":"span","markDefs":[],"marks":[],"text":"($s$) ↔ "},{"_key":"ip9ZSUgFyzGIsQgTfx59BW","_type":"span","markDefs":[],"marks":["strong"],"text":"Angular Displacement"},{"_key":"ip9ZSUgFyzGIsQgTfx59DE","_type":"span","markDefs":[],"marks":[],"text":"($\\theta$)"}],"level":1,"listItem":"bullet","markDefs":[],"style":"normal"},{"_key":"block_57","_type":"block","asset":null,"children":[{"_key":"ip9ZSUgFyzGIsQgTfx59Ew","_type":"span","markDefs":[],"marks":["strong"],"text":"Velocity"},{"_key":"ip9ZSUgFyzGIsQgTfx59Ge","_type":"span","markDefs":[],"marks":[],"text":"($v$) ↔ "},{"_key":"ip9ZSUgFyzGIsQgTfx59IM","_type":"span","markDefs":[],"marks":["strong"],"text":"Angular Velocity"},{"_key":"ip9ZSUgFyzGIsQgTfx59K4","_type":"span","markDefs":[],"marks":[],"text":"($\\omega$)"}],"level":1,"listItem":"bullet","markDefs":[],"style":"normal"},{"_key":"block_58","_type":"block","asset":null,"children":[{"_key":"ip9ZSUgFyzGIsQgTfx59Lm","_type":"span","markDefs":[],"marks":["strong"],"text":"Acceleration"},{"_key":"ip9ZSUgFyzGIsQgTfx59NU","_type":"span","markDefs":[],"marks":[],"text":"($a$) ↔ "},{"_key":"ip9ZSUgFyzGIsQgTfx59PC","_type":"span","markDefs":[],"marks":["strong"],"text":"Angular Acceleration"},{"_key":"ip9ZSUgFyzGIsQgTfx59Qu","_type":"span","markDefs":[],"marks":[],"text":"($\\alpha$)"}],"level":1,"listItem":"bullet","markDefs":[],"style":"normal"}] ![](https://cdn.sanity.io/images/w7j7fz60/production/5e460b0826fa90ba6d02e459a8cd4326c2559baa-756x788.png) ## Equations of Rotational Motion [block_59] The equations of **rotational** motion mirror those of **linear** motion, with angular quantities replacing linear ones. ### Rotational Motion Equations [block_61] $$\theta = \omega_i t + \frac{1}{2} \alpha t^2$$ $$\omega = \omega_i + \alpha t$$ $$\omega^2 = \omega_i^2 + 2\alpha \theta$$ [{"_key":"block_71","_type":"block","asset":null,"children":[{"_key":"5f8b618aa3d3","_type":"span","markDefs":[],"marks":[],"text":"Always express angles in "},{"_key":"645e63fa8058","_type":"span","markDefs":[],"marks":["strong"],"text":"radians "},{"_key":"4505242c2c5c","_type":"span","markDefs":[],"marks":[],"text":"when using these equations."}],"markDefs":[],"style":"normal"}] A wheel starts from rest and accelerates at $2 \, \text{rad s}^{-2}$ for $5 \, \text{s}$. How much angular displacement does it undergo? * **Given**: $\omega_i = 0$, $\alpha = 2 \, \text{rad s}^{-2}$, $t = 5 \, \text{s}$ * **Use**: $\theta = \omega_i t + \frac{1}{2} \alpha t^2$ $$ \theta = 0 + \frac{1}{2} \times 2 \times 5^2 = 25 \, \text{rad} $$ ## Bridging Linear and Rotational Motion [block_72] **Rotational **motion is deeply connected to **linear **motion. For an object rotating in a circle of radius $r$: 1. **Linear Velocity**: $v = \omega r$ 2. **Linear Acceleration**: $a = \alpha r$ [{"_key":"block_78","_type":"block","asset":null,"children":[{"_key":"72ceb4952a56","_type":"span","markDefs":[],"marks":[],"text":"Students often confuse angular and linear quantities. "}],"level":1,"listItem":"bullet","markDefs":[],"style":"normal"},{"_key":"9f057e6b2c5b","_type":"block","asset":null,"children":[{"_key":"c680462ebdf5","_type":"span","markDefs":[],"marks":[],"text":"Remember, "},{"_key":"1e73be06840d","_type":"span","markDefs":[],"marks":["strong"],"text":"angular velocity"},{"_key":"10a29bfd5c0d","_type":"span","markDefs":[],"marks":[],"text":" ($\\omega$) is the same for all points on a rotating object, but "},{"_key":"f172a215351b","_type":"span","markDefs":[],"marks":["strong"],"text":"linear velocity"},{"_key":"159fac453b6f","_type":"span","markDefs":[],"marks":[],"text":" ($v$) varies with distance from the axis."}],"level":1,"listItem":"bullet","markDefs":[],"style":"normal"}] [{"_key":"block_84","_type":"block","asset":null,"children":[{"_key":"15f9a3d0fb36","_type":"span","marks":[],"text":""}],"markDefs":[],"style":"normal"},{"_key":"block_85","_type":"block","asset":null,"children":[{"_key":"7479420f89c1","_type":"span","markDefs":[],"marks":[],"text":"What are the conditions for an object to be in equilibrium?"}],"level":1,"listItem":"bullet","markDefs":[],"style":"normal"},{"_key":"block_86","_type":"block","asset":null,"children":[{"_key":"ee0b68249442","_type":"span","markDefs":[],"marks":[],"text":"How do angular velocity and linear velocity relate for a point on a rotating object?"}],"level":1,"listItem":"bullet","markDefs":[],"style":"normal"},{"_key":"block_87","_type":"block","asset":null,"children":[{"_key":"122afcdef103","_type":"span","markDefs":[],"marks":[],"text":"Can you derive the rotational motion equations from their linear counterparts?"}],"level":1,"listItem":"bullet","markDefs":[],"style":"normal"}] ## [block_79]