Unit Circle Definitions and Exact Trigonometric Ratios

The Unit Circle

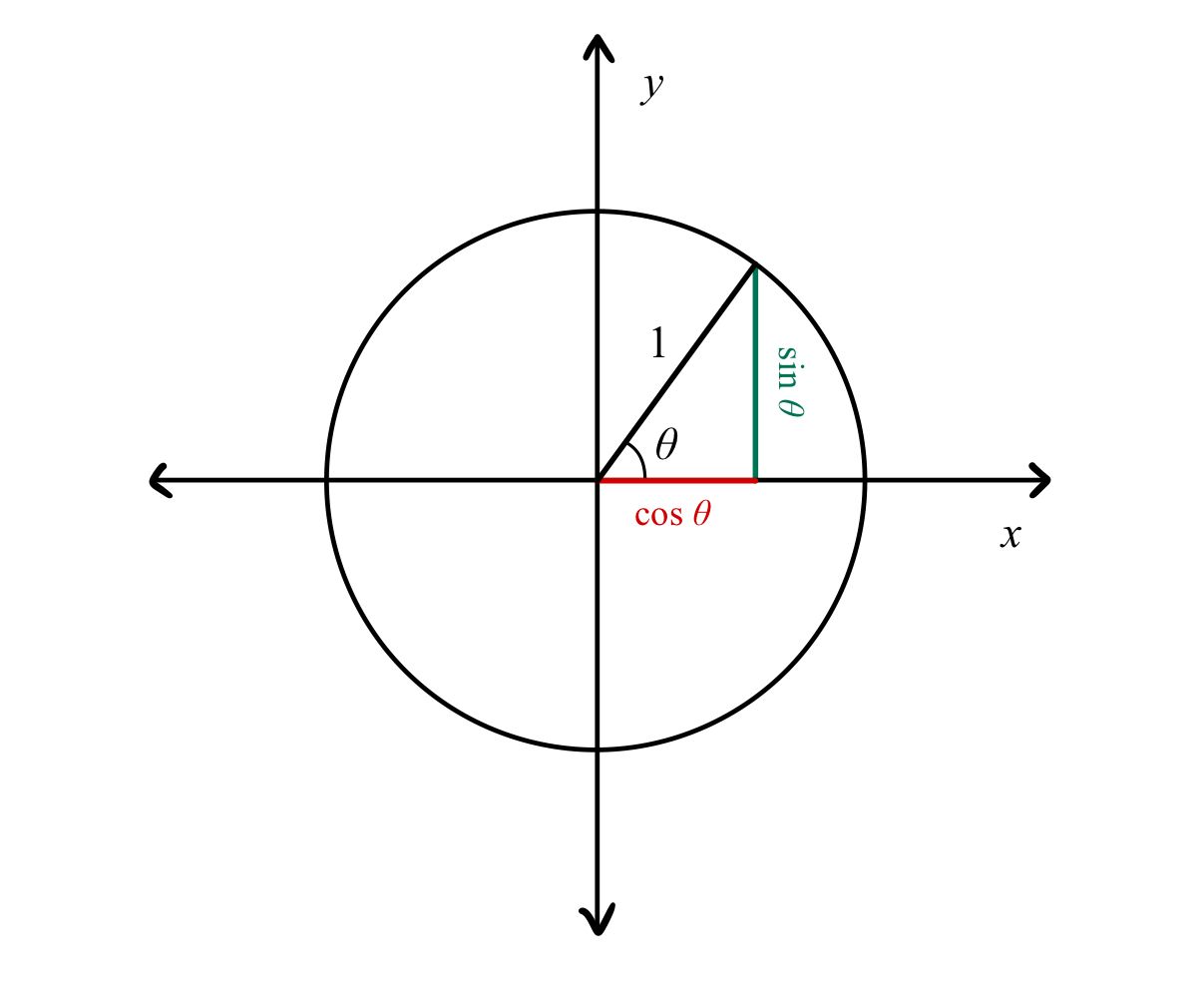
The unit circle is a circle with radius 1 centered at the origin (0,0).

On the unit circle:

• The x-coordinate is $\cos \theta$
• The y-coordinate is $\sin \theta$
• The slope of the radius line is $\tan \theta = \frac{\sin \theta}{\cos \theta}$

Unit Circle and Ratios

Depending on which quadrant $\theta$ is in, the values of $\sin \theta, \cos \theta, \tan \theta $ may change sign.

• Since $\sin\theta$ is correlated with the $y$-value of the point on the unit circle, $\sin\theta$ is positive in the first and second quadrants ($y>0$), and negative in the third and fourth ($y<0$).
• Since $\cos\theta$ is correlated with the $x$-value of the point on the unit circle, $\cos\theta$ is positive in the first and fourth quadrants ($x>0$), and negative in the second and third ($x<0$).
• Since $\tan\theta$ is correlated with the slope of the line to the point on the unit circle, $\tan\theta$ is positive in the first and third quadrants ($y/x > 0$) and negative in the second and fourth quadrants ($y/x < 0$).

Tip

Some students use the mnemonic "All Students Take Calculus" for which trigonometric functions are positive in which quadrants.

1. All functions are positive in the first quadrant.
2. Sine is positive in the second quadrant.
3. Tangent is positive in the third quadrant.
4. Cosine is positive in the fourth quadrant.

The Ambiguous Case of the Sine Rule

The sine rule states: $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

When using the sine rule to solve for an angle, we sometimes get two possible solutions. This is called the ambiguous case.

The ambiguous case occurs when:

• You're solving for an angle using the sine rule
• The angle you're solving for could be acute or obtuse
• The given side is shorter than the side opposite to the given angle

Understanding When Two Solutions Exist

For the ambiguous case to be possible:

1. The side opposite to the unknown angle must be shorter than the side opposite to the known angle
2. The known angle must be less than 90°
3. The ratio $\frac{b \sin A}{a}$ must be less than or equal to 1

Pythagorean Identity

Let's start with this triangle again:

Let's label the sides $o$, $a$, and $h$ for brevity.

Now, with the Pythagorean theorem, we can write:

$$o^2 + a^2 = h^2$$

Dividing both sides by $h^2$ we get:

$$\frac{o^2}{h^2} + \frac{a^2}{h^2} = \frac{h^2}{h^2} \to (\frac{o}h)^2+(\frac{a}h)^2=1$$

But $\sin\theta = \frac{o}h$ and $\cos\theta = \frac{a}h$. So, the above simplifies to:

$\cos^2 θ + \sin^2 θ = 1$

This is the Pythagorean identity in trigonometry.

Solutions to Equations

Graphical Method

Solving trigonometric equations graphically involves plotting the functions on both sides of the equation and finding their intersection points. This is usually done on paper 2, where you get a calculator to do this.

For example, to solve $0.866\sin(1.46x + 2.15) = 2.14\cos(0.559x - 1.23) - 0.291, 0 \leq x \leq 2\pi$, we can simply plot both sides:

In the graph above, the intersections of $y = 0.866\sin(1.46x + 2.15)$ and $y = 2.14\cos(0.559x - 1.23) - 0.291$ occur at $x \approx 0.157$ and $x \approx 4.00$. So, those are the solutions to our equation.

General Solutions

Usually, you will have a finite interval to give your answer in, but since angles give the same value every revolution, there are technically infinite solutions

The above is called a general solution

A general solution includes all possible solutions to a trigonometric equation, typically expressed using the variable $n$ to represent any integer.

For example, the general solution to $\sin x = \frac{1}{2}$ is:

$x = \frac{\pi}{6} + 2\pi n$ or $x = \pi - \frac{\pi}{6} + 2\pi n$, where $n$ is any integer.