Tree and Cycle Algorithms in Graph Theory
Undirected Graphs and Basic Concepts
- In graph theory, an undirected graph is a set of vertices connected by edges, where the edges have no direction.
- This forms the basis for many important algorithms in computer science and operations research.
Key concepts include:
- Walk: A sequence of vertices and edges, allowing repetition
- Trail: A walk with no repeated edges
- Path: A walk with no repeated vertices
- Circuit: A trail that starts and ends at the same vertex
- Cycle: A path that starts and ends at the same vertex (a simple circuit)
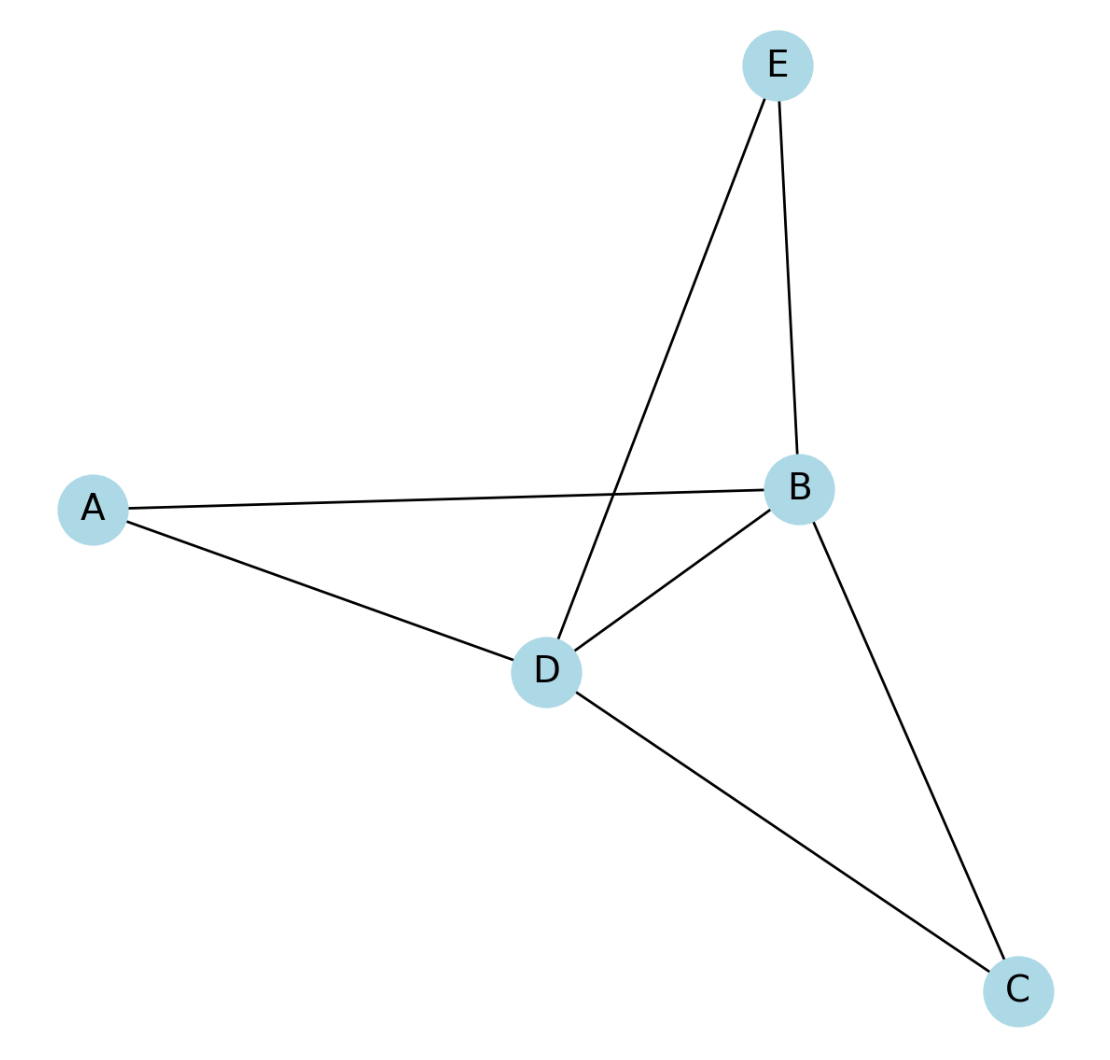
Consider the undirected graph above.
- Walk: A sequence of vertices where consecutive vertices are connected by an edge.
- Example: \( A \to B \to C \to D \to B \to E \)
- Trail: A walk in which no edge is repeated.
- Example: \( A \to B \to C \to D \to E \)
- Path: A trail in which no vertex is repeated.
- Example: \( A \to B \to D \to E \)
- Circuit: A trail that starts and ends at the same vertex.
- Example: \( A \to B \to C \to D \to B \to A \)
- Cycle: A path that starts and ends at the same vertex with no repeated edges or vertices (except the start/end vertex).
- Example: \( A \to B \to C \to D \to A \)
Eulerian Trails and Circuits
- An Eulerian trail is a trail that uses every edge in a graph exactly once.
- An Eulerian circuit is an Eulerian trail that starts and ends at the same vertex.
To determine if an Eulerian trail or circuit exists:
- For an Eulerian circuit: All vertices must have even degree.
- For an Eulerian trail: Exactly two vertices must have odd degree (these will be the start and end vertices).
The degree of a vertex is the number of edges connected to it.
Hamiltonian Paths and Cycles
- A Hamiltonian path is a path that visits each vertex exactly once.
- A Hamiltonian cycle is a Hamiltonian path that returns to the starting vertex.
Unlike Eulerian trails, there's no simple rule to determine if a Hamiltonian path or cycle exists in a general graph. This leads to the famous Traveling Salesman Problem, which we'll discuss later.
Common MistakeStudents often confuse Eulerian and Hamiltonian concepts. Remember: Eulerian deals with using all edges once, while Hamiltonian deals with visiting all vertices once.
ExampleConsider the following graph with vertices:
$$V=\{A, B, C, D, E, F\}$$
and edges:
$$E=\{(A, B),(A, C),(B, D),(B, E),(C, D),(C, F),(D, E),(E, F)\}$$
A valid Hamiltonian Path for this graph could be:
$$A \rightarrow B \rightarrow E \rightarrow D \rightarrow C \rightarrow F$$
Each vertex is visited exactly once, but the path does not necessarily return to $\mathbf{A}$.
Using the same graph as above, a possible Hamiltonian Cycle is:
$$
A \rightarrow B \rightarrow E \rightarrow D \rightarrow C \rightarrow F \rightarrow A
$$
This cycle starts at A, visits every vertex exactly once, and returns to A.
Minimum Spanning Tree (MST) Algorithms
- A spanning tree of a graph is a tree that includes all vertices of the graph.
- A minimum spanning tree is a spanning tree with the lowest total edge weight.
Kruskal's Algorithm
Kruskal's algorithm finds an MST by adding the lowest-weight edge that doesn't create a cycle, until all vertices are connected.
Steps:
- Sort all edges by weight (ascending).
- Start with an empty set of edges.
- For each edge, from lowest to highest weight:
- If adding this edge doesn't create a cycle, add it.
- If it creates a cycle, skip it.
- Stop when you have $n-1$ edges, where $n$ is the number of vertices.
Prim's Algorithm
Prim's algorithm starts with a single vertex and grows the MST by adding the lowest-weight edge connecting the tree to a new vertex at each step.
Steps:
- Start with any vertex
- Find the lowest-weight edge connecting the tree to a new vertex
- Add this edge and vertex to the tree
- Repeat steps 2-3 until all vertices are in the tree
Prim's algorithm is often faster for dense graphs, while Kruskal's can be better for sparse graphs.
Chinese Postman Problem
- The Chinese Postman Problem involves finding the shortest route that traverses every edge in a weighted graph at least once, returning to the starting point.
- For graphs with all even-degree vertices, an Eulerian circuit is the optimal solution.
For graphs with odd-degree vertices:
- Identify odd-degree vertices
- Find all possible pairings of these vertices
- For each pairing, add the shortest path between each pair to the graph
- Choose the pairing that adds the least total weight
- Find an Eulerian circuit in the modified graph
The IB curriculum typically limits this to graphs with up to 4 odd vertices.
ExampleA mail carrier needs to deliver mail along roads in a neighborhood. The roads are represented as edges in a weighted graph, where the vertices represent intersections and the edge weights represent the distances (in km) between them.
Consider the following graph with weighted edges:
Graph Representation
Vertices:
$$V = \{ A, B, C, D, E \}$$
Edges with Weights:
$$E = \{ (A, B, 4), (A, C, 2), (B, C, 3), (B, D, 5), (C, D, 3), (C, E, 6), (D, E, 4) \}$$
The graph is not Eulerian since it has odd-degree vertices.
To solve the Chinese Postman Problem, we follow these steps:
Step 1: Identify Odd-Degree Vertices
- Degree of A = 2 (even)
- Degree of B = 3 (odd)
- Degree of C = 4 (even)
- Degree of D = 3 (odd)
- Degree of E = 2 (even)
Odd-degree vertices: B, D
Step 2: Find the Shortest Path Between Odd-Degree Vertices
The shortest path between B and D is B → C → D with total weight 3 + 3 = 6.
Step 3: Duplicate the Shortest Path
To make all vertices have even degrees, we duplicate the shortest path B → C → D in the graph.
Step 4: Find an Eulerian Circuit
The modified graph now has all even-degree vertices, allowing us to find an Eulerian circuit. The Eulerian circuit ensures that every road (edge) is covered at least once while minimizing the total distance.
Traveling Salesman Problem
The Traveling Salesman Problem (TSP) involves finding the shortest Hamiltonian cycle in a weighted complete graph.
HintThis is an NP-hard problem, meaning no efficient algorithm is known for solving it exactly for large instances.
Nearest Neighbor Algorithm (Upper Bound)
This heuristic provides an upper bound for the TSP:
- Start at any vertex
- Repeatedly move to the nearest unvisited vertex
- Return to the start when all vertices are visited
This doesn't guarantee the optimal solution but is quick to compute.
Deleted Vertex Algorithm (Lower Bound)
This provides a lower bound for the TSP:
- Delete any vertex from the graph
- Find the MST of the remaining graph
- Add the two cheapest edges connecting the deleted vertex to the MST
- The total weight of this tree is a lower bound for the TSP
Remember, these algorithms provide bounds, not necessarily the optimal solution. The exact solution for large TSP instances is computationally infeasible.