RevisionDojo

Question 1

Skill question

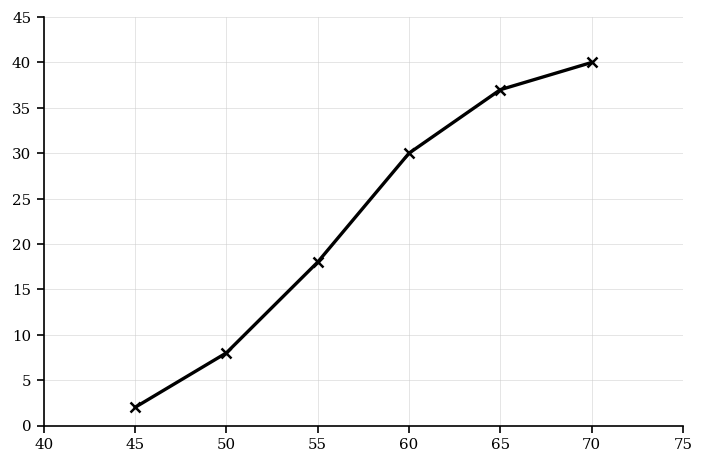
A cumulative frequency graph for 40 adults’ weights (kg) is drawn through the points below.

Data (points on the cumulative frequency curve):

Upper weight (kg)	Cumulative frequency
45	2
50	8
55	18
60	30
65	37
70	40

Cumulative frequency graph for 40 adults

Estimate $Q_1$ , $Q_3$ , and the IQR. Give answers to 1 decimal place if needed.

[6]

Question 2

Skill question

The cumulative frequency graph for metal rod lengths (cm) passes through the points below.

Upper length (cm)	Cumulative frequency
24	3
28	10
32	24
36	44
40	61
44	69
48	72

Cumulative frequency graph

Estimate $Q_1$ , the median, $Q_3$ , and the IQR. Give answers to 1 decimal place where necessary.

[6]

Question 3

Skill question

Heights (cm) of 48 seedlings are displayed with a cumulative frequency graph through the points below.

Data (points on the cumulative frequency graph):

Upper height (cm)	Cumulative frequency
54	4
58	12
62	24
66	34
70	42
74	48

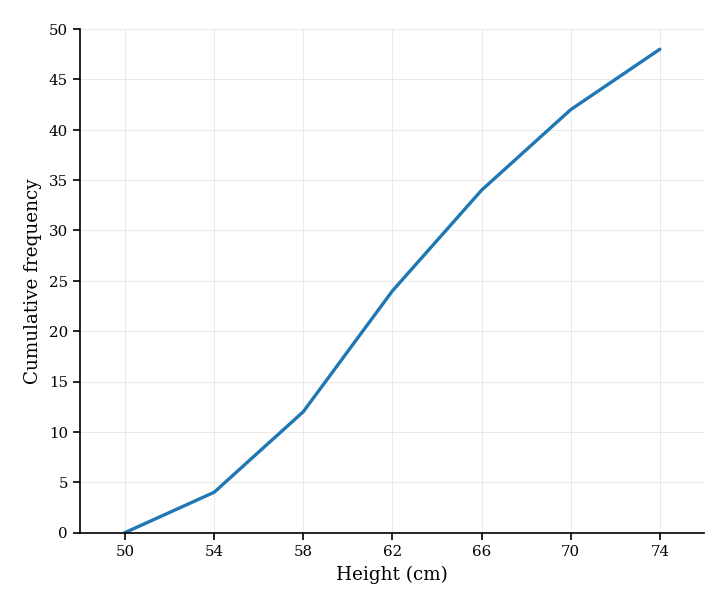
Cumulative frequency graph of seedling heights

Estimate $Q_1$ , median, $Q_3$ , and the IQR. Give answers to 1 decimal place where necessary.

[5]

Question 4

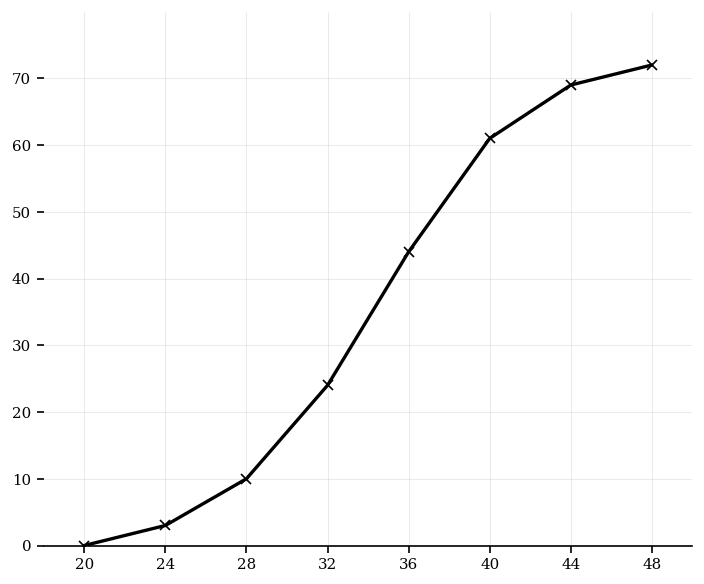
Skill question

Leaf lengths (cm) for 60 leaves were grouped and a cumulative frequency curve was drawn through the points below.

Data (points on the cumulative frequency curve):

Upper length (cm)	Cumulative frequency
4	5
6	14
8	30
10	44
12	54
14	60

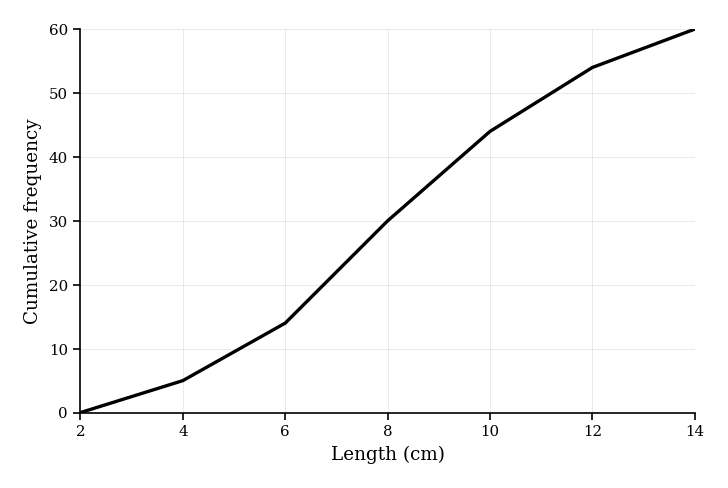
Estimate the interquartile range (IQR). Give your answer to 1 decimal place.

[5]

Question 5

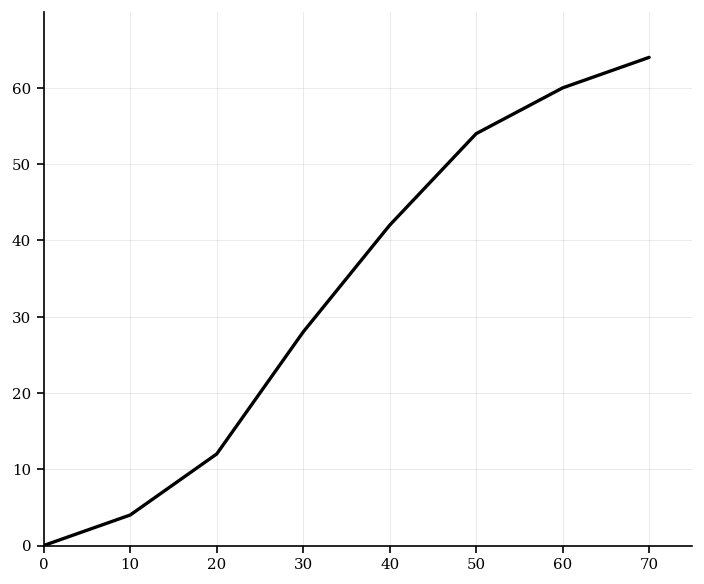
Skill question

The cumulative frequency graph of test scores (out of 60) is drawn by plotting the points below and joining them with straight segments.

Data (points on the cumulative frequency curve):

Upper score	Cumulative frequency
10	4
20	10
30	20
40	32
50	42
60	50

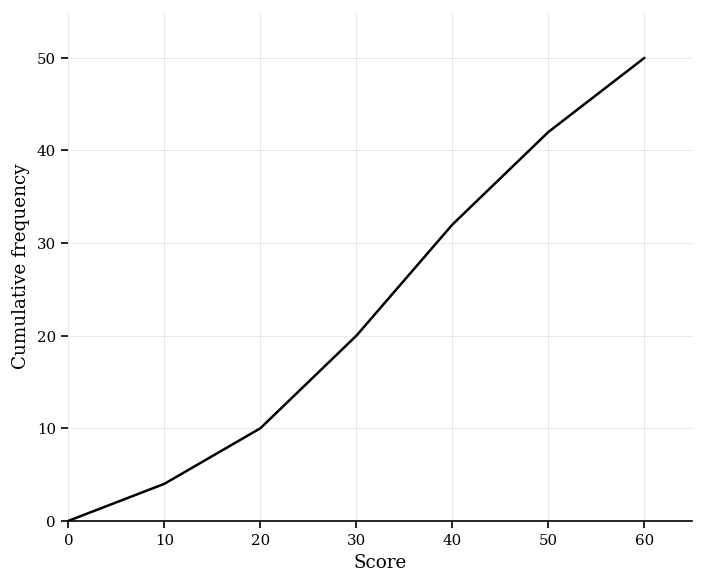
Cumulative frequency graph of test scores

Estimate $Q_1$ , the median, $Q_3$ , and the interquartile range (IQR). Give answers to 1 decimal place where necessary.

[6]

Question 6

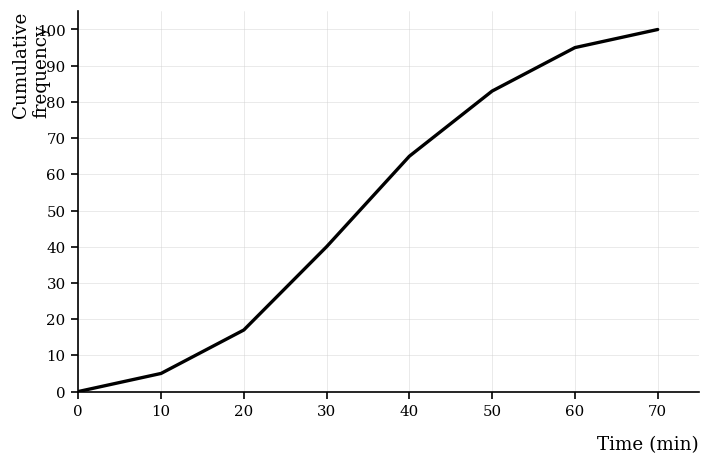
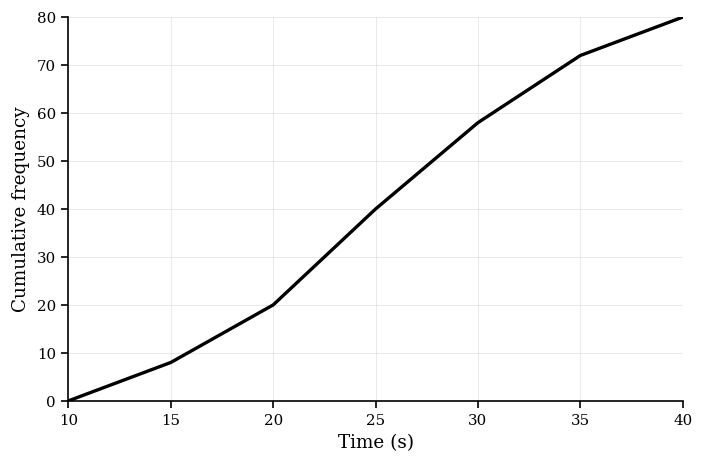
Skill question

A cumulative frequency graph for 50 task completion times (minutes) includes a zero-frequency class. The graph connects the points below with straight line segments.

Data (points on the cumulative frequency graph):

Upper time (min)	Cumulative frequency
5	6
10	20
12	20
20	40
30	50

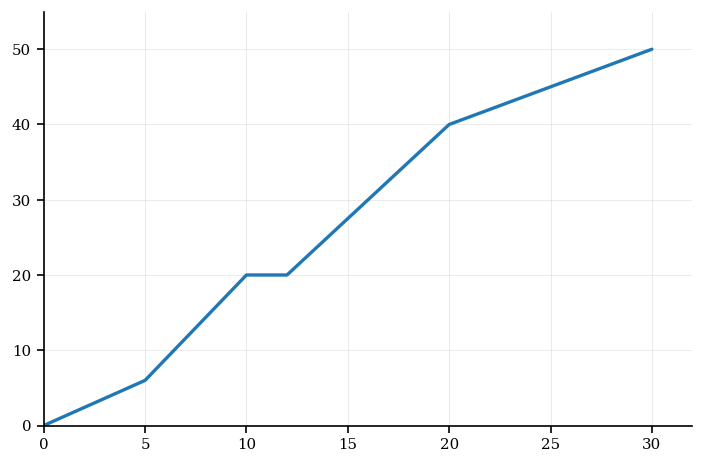
Cumulative frequency graph showing task completion times

Estimate the median and the interquartile range (IQR). Give your answers to 1 decimal place where necessary.

[7]

Question 7

Skill question

The cumulative frequency graph for ages (years) of $64$ museum visitors passes through the points below.

Data (points on the cumulative frequency curve):

Upper age (years)	Cumulative frequency
$10$	$4$
$20$	$12$
$30$	$28$
$40$	$42$
$50$	$54$
$60$	$60$
$70$	$64$

Cumulative frequency graph

Estimate the median and IQR. Give answers to 1 decimal place where necessary.

[6]

Question 8

Skill question

Reaction times (ms) for 200 participants are summarized by the cumulative frequency curve through the points below.

Data (points on the cumulative frequency curve):

Upper time (ms)	Cumulative frequency
150	8
200	30
250	80
300	140
350	178
400	194
450	200

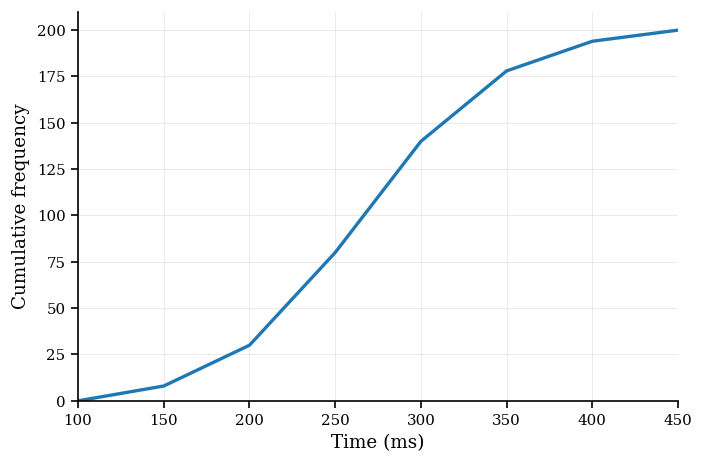
Cumulative frequency graph of reaction times

Estimate the median and the IQR. Give answers to 1 decimal place where necessary.

[6]

Question 9

Skill question

The cumulative frequency graph for 100 commuters’ travel times (minutes) passes through the points below.

Time (min)	Cumulative frequency
10	5
20	17
30	40
40	65
50	83
60	95
70	100

Cumulative frequency graph of commuters' travel times

Estimate the median and IQR. Give answers to 1 decimal place.

[6]

Question 10

Skill question

The cumulative frequency graph for car speeds (km/h) is based on unequal class widths and passes through the points below.

Data (points on the cumulative frequency curve):

Upper speed (km/h)	Cumulative frequency
120	8
130	20
150	50
170	75
200	90

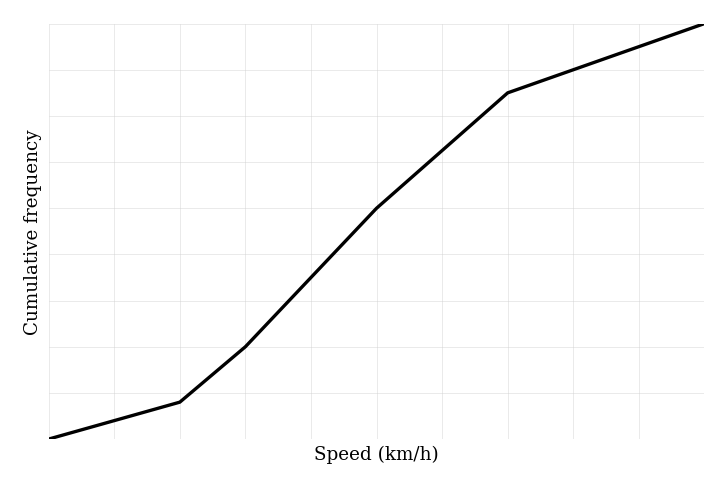
Cumulative frequency graph of car speeds

Estimate $Q_1$ , the median, $Q_3$ , and the IQR. Give answers to 1 decimal place where necessary.

[9]

Question 11

Skill question

The cumulative frequency graph for 80 athletes’ sprint times (in seconds) is drawn through the points below.

Time ( $t$ )	Cumulative frequency
15	8
20	20
25	40
30	58
35	72
40	80

Cumulative frequency graph

Estimate the median and the interquartile range (IQR). Give answers to 1 decimal place where necessary.

[6]

Question 12

Skill question

Two classes sat the same test. Their cumulative frequency graphs are summarised by the points below.

Class A data (points on the cumulative frequency curve):

Upper mark	Cumulative frequency
20	8
30	22
40	40
50	52
60	60

Class B data (points on the cumulative frequency curve):

Upper mark	Cumulative frequency
20	5
30	18
40	36
50	54
60	60

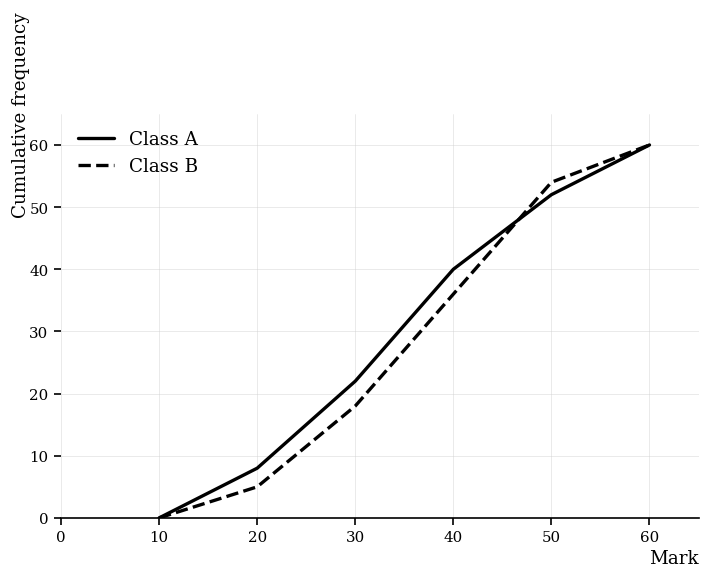
Cumulative frequency graphs for Class A (solid) and Class B (dashed) on axes mark vs cumulative frequency

For each class, estimate the IQR, then state which class has the larger IQR. Give answers to 1 decimal place where necessary.

[8]

Question Type 3: Finding the quartiles using the cumulative frequency graph Exercises