RevisionDojo

Question 1

Masses of parcels (kg) are grouped below. Construct a less-than cumulative frequency graph and estimate the interquartile range (IQR).

Data:

Class interval (kg)	Frequency
0–2	6
2–4	10
4–6	18
6–8	9
8–12	7

[7]

Question 2

Construct a cumulative frequency graph for the heights (cm) of 35 students and hence estimate the median height. Use the class upper boundaries for plotting.

Data (heights in cm):

Class interval	Frequency
140–150	4
150–160	7
160–170	12
170–180	9
180–190	3

[5]

Question 3

Travel times to work (minutes) for $40$ commuters are grouped as follows.

Construct a cumulative frequency graph and estimate how many commuters take more than $45$ minutes to travel.

Data:

Class interval (min)	Frequency
$10–20$	$5$
$20–30$	$9$
$30–40$	$14$
$40–50$	$8$
$50–60$	$4$

[6]

Question 4

Reaction times (s) in an experiment are grouped as below. Construct a cumulative frequency graph and estimate the 90th percentile.

Data:

Class interval (s)	Frequency
0.2–0.3	3
0.3–0.4	8
0.4–0.5	14
0.5–0.7	10
0.7–0.9	5

[4]

Question 5

The cumulative frequency graph of test scores (out of 100) is summarized by the points below (upper class boundaries with cumulative frequencies). Use the graph to estimate the interquartile range (IQR).

The table below shows the data used to plot the ogive:

Class interval	Upper boundary	Cumulative frequency
0–20	20	8
20–40	40	23
40–60	60	45
60–80	80	72
80–100	100	80

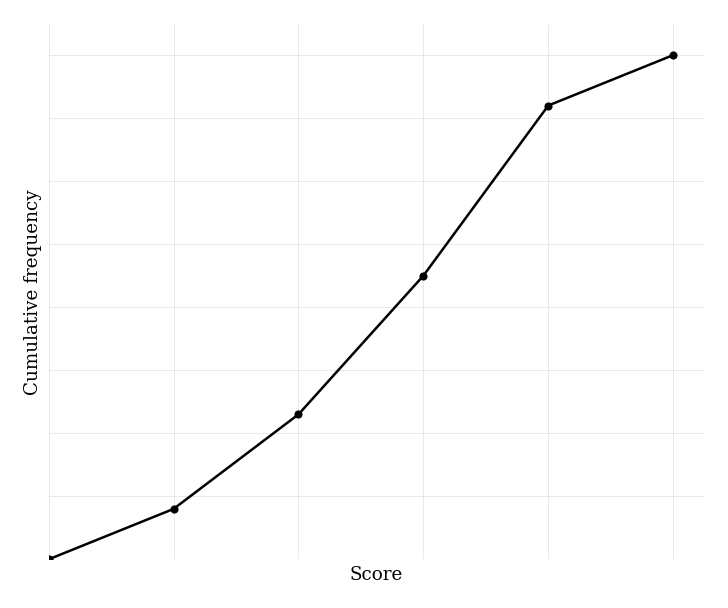
Cumulative Frequency Graph

[5]

Question 6

Lengths of parts (mm) are grouped as follows. Construct a less-than cumulative frequency graph and estimate the median length.

Data:

Class interval (mm)	Frequency
50–55	4
55–60	10
60–65	12
65–70	8
70–80	6

[5]

Question 7

A cumulative frequency graph for the weights (kg) of 60 packages is represented by the points below. Use it to construct the estimated frequency distribution table for each class interval.

Data (less-than ogive points):

Class interval (kg)	Upper boundary	Cumulative frequency
40–50	50	3
50–60	60	11
60–70	70	26
70–80	80	44
80–90	90	57
90–100	100	60

[2]

Question 8

The lifetimes of 100 light bulbs (hours) are summarised by the cumulative frequency points below. Using the ogive, estimate the median lifetime.

Data (ogive points):

Class interval (hours)	Upper boundary	Cumulative frequency
500–600	600	5
600–700	700	18
700–800	800	40
800–900	900	68
900–1100	1100	100

[4]

Question 9

The cumulative frequency of house prices (in thousands of dollars) is shown in the table below. Use it to construct the estimated frequency distribution table for the given classes.

Data (ogive points):

Price ( $P$ ) ($1000s)	Upper boundary	Cumulative frequency
$100 < P \le 150$	150	4
$150 < P \le 200$	200	12
$200 < P \le 250$	250	27
$250 < P \le 300$	300	41
$300 < P \le 400$	400	59
$400 < P \le 600$	600	80

[3]

Question 10

Weekly study hours for 35 students are grouped below.

Class interval (hours)	Frequency
$0 \leq t < 5$	2
$5 \leq t < 10$	5
$10 \leq t < 15$	12
$15 \leq t < 20$	9
$20 \leq t < 30$	7

Construct a cumulative frequency graph and estimate the 65th percentile, $P_{65}$ .

[6]

Question 11

The cumulative frequency table below shows the monthly expenses (in dollars) of a group of students.

Class interval	Upper boundary	Cumulative frequency
$200-300$	$300$	$5$
$300-400$	$400$	$17$
$400-500$	$500$	$35$
$500-700$	$700$	$60$
$700-1000$	$1000$	$80$

Determine which class interval has the highest frequency.

[3]

Question 12

The cumulative frequency data for exam scores is summarized in the table below. Use it to reconstruct the estimated frequency distribution table for the 10-mark wide classes.

Data:

Class interval	Upper boundary	Cumulative frequency
0–10	10	6
10–20	20	18
20–30	30	33
30–40	40	55
40–50	50	78
50–60	60	96
60–70	70	108
70–80	80	116
80–90	90	120
90–100	100	120

[3]

Question 13

Daily step counts (in thousands) for 40 days are grouped below. Construct a cumulative frequency graph and estimate the lower quartile $Q_1$ .

Data:

Class interval (thousand steps)	Frequency
0–2	3
2–4	7
4–6	15
6–8	11
8–12	4

[6]

Question Type 2: Constructing cumilative frequency graphs given the frequency distribution table Exercises