Single-Slit Diffraction
Understanding Single-Slit Diffraction
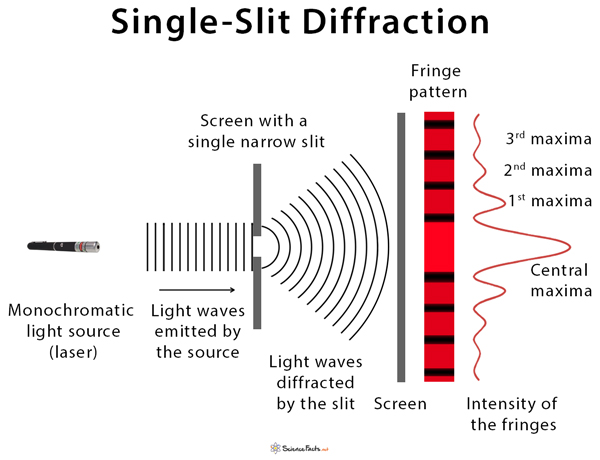
- When light passes through a single narrow slit, it spreads out and forms a diffraction pattern on a screen.
- This pattern consists of a central bright fringe flanked by dimmer and narrower fringes.
The central maximum is the brightest and widest part of the pattern, while the intensity of the fringes decreases as you move away from the center.
Mathematical Description of Diffraction
The position of the first minimum in the diffraction pattern is determined by the equation:
$$\theta = \frac{\lambda}{b}$$
where:
- $\theta$ is the angle of the first minimum
- $\lambda$ is the wavelength of the light
- $b$ is the width of the slit
This equation shows that the angle of the first minimum depends on the ratio of the wavelength to the slit width.
Smaller slits or longer wavelengths result in wider diffraction patterns, while larger slits or shorter wavelengths produce narrower patterns.
Intensity Patterns
- The intensity of the diffraction pattern is highest at the central maximum and decreases for the secondary maxima.
- The first secondary maximum is about 4.5% as bright as the central maximum.
- If red light with a wavelength of $700 \, \text{nm}$ passes through a slit of width $1.4 \times 10^{-5} \, \text{m}$, the first minimum occurs at an angle of $0.05 \, \text{rad}$.
- This confirms the relationship $\theta = \frac{\lambda}{b}$.
Multiple Slits and Diffraction Gratings
Double-Slit Interference
- In a double-slit experiment, light passing through two slits creates an interference pattern of bright and dark fringes.
- The condition for constructive interference (bright fringes) is: $$d \sin \theta = n \lambda$$ where:
- $d$ is the distance between the slits
- $\theta$ is the angle of the fringe
- $n$ is the order of the fringe (an integer)
- $\lambda$ is the wavelength of the light
In a double-slit experiment with a slit separation of $0.15 \, \text{mm}$ and a screen $1.3 \, \text{m}$ away, the fringe separation for light of wavelength $570 \, \text{nm}$ is $4.95 \, \text{mm}$.
Diffraction Gratings
- A diffraction grating consists of many closely spaced slits, producing a more defined interference pattern.
- The condition for constructive interference is the same as for double slits:
$$d \sin \theta = n \lambda$$
The advantage of a diffraction grating is that the maxima are sharper and brighter, making them easier to measure.
A diffraction grating with $600$ lines per mm has a slit separation of $d = \frac{1}{600} \, \text{mm} = 1.67 \times 10^{-6} \, \text{m}$.
For light of wavelength $680 \, \text{nm}$, the first-order maximum occurs at an angle of $24.1^\circ$.
Combined Patterns: Single-Slit Diffraction Modulating Double-Slit Interference
- In a real double-slit experiment, the slits have a finite width, causing the single-slit diffraction pattern to modulate the double-slit interference pattern.
- This means the intensity of the interference fringes is enveloped by the diffraction pattern.
The central maximum of the diffraction pattern contains several interference fringes, but the intensity of the fringes decreases towards the edges of the diffraction envelope.
If the third-order maximum of the double-slit pattern coincides with the first minimum of the single-slit pattern, it will not be visible because the intensity at that point is zero.
Wave Interference
Intensity and Wavelength: Relationship Between Slit Width, Wavelength, and Diffraction Pattern Brightness
The intensity of the diffraction pattern depends on the slit width and the wavelength of the light.
Key Relationships
- Wider Slits:
- Allow more light to pass through, increasing the overall intensity of the pattern.
- However, they also decrease the angular width of the central maximum.
- Longer Wavelengths:
- Result in wider diffraction patterns, spreading the light over a larger area and reducing the intensity of the central maximum.
- Narrower Slits:
- Produce wider diffraction patterns but reduce the overall intensity because less light passes through.
Students often confuse the effects of slit width and wavelength. Remember:
- Increasing the slit width narrows the diffraction pattern but increases its intensity.
- Increasing the wavelength widens the pattern but decreases its intensity.