IB Mathematics Applications & Interpretation Question Type 7: Given Values of Events, Using Diagrams to Interpret Probabilities Exercises

In a Venn diagram of four mutually overlapping sets, it is found that $P(\text{none of the events})=0.1$. If $P(\text{at least one})=0.9$, verify by interpretation of the diagram that these two values sum to 1.

In a class of 50 students, 30 study Mathematics, 20 study Science and 10 study both. Using a Venn diagram approach, calculate the probability that a student studies neither subject.

A tree diagram models three outcomes on the first roll of a loaded die: $1\text{–}3$ with a probability of $0.5$, $4\text{–}5$ with a probability of $0.3$, and $6$ with a probability of $0.2$. If $1\text{–}3$ occurs, the second roll has a success probability of $0.4$; otherwise, the success probability is $0.6$. Find the probability of success in the second roll.

A probability tree for a medical test shows that the disease prevalence in a population is $5\%$. The test provides a true positive result with a probability of $90\%$ and a false positive result with a probability of $8\%$.

Calculate the probability that a randomly selected person from this population tests positive.

A probability tree describes two independent stages: stage 1 succeeds with probability 0.6 and fails with probability 0.4; stage 2 succeeds with probability 0.7 and fails with probability 0.3. Calculate the probability that at least one stage succeeds.

Given two events $A$ and $B$ with $P(A)=0.5$, $P(B)=0.6$, and $P(A\cup B)=0.8$, use a Venn diagram to find $P(A\cap B)$.

In a survey, 40% of people exercise regularly, 25% follow a diet plan, and 15% do both. What is the probability that a person exercises but does not follow the diet plan? Illustrate with a Venn diagram.

In a survey of 100 people, 60 like tea ($T$), 45 like coffee ($C$) and 20 like both. Using a Venn diagram interpretation, find the probability that a randomly chosen person likes coffee.

A rectangular probability diagram is partitioned into regions for events $X$ and $Y$ as shown below.

Draw on this

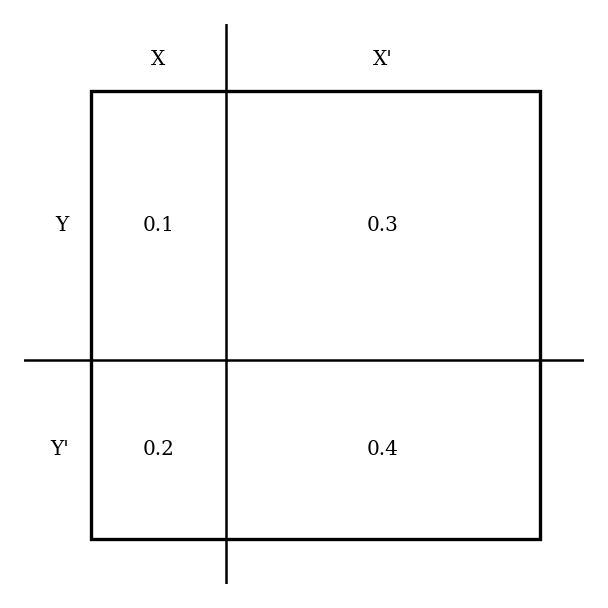
The joint probabilities are given as $P(X\cap Y)=0.1$, $P(X\cap Y^{\prime })=0.2$, and $P(X^{\prime }\cap Y)=0.3$.

Find $P(X^{\prime }\cup Y)$.

The following Venn diagram shows two events $A$ and $B$ in a sample space $S$, where $P(A)=0.4$, $P(B)=0.5$, and $P(A\cap B)=0.2$.

Draw on this

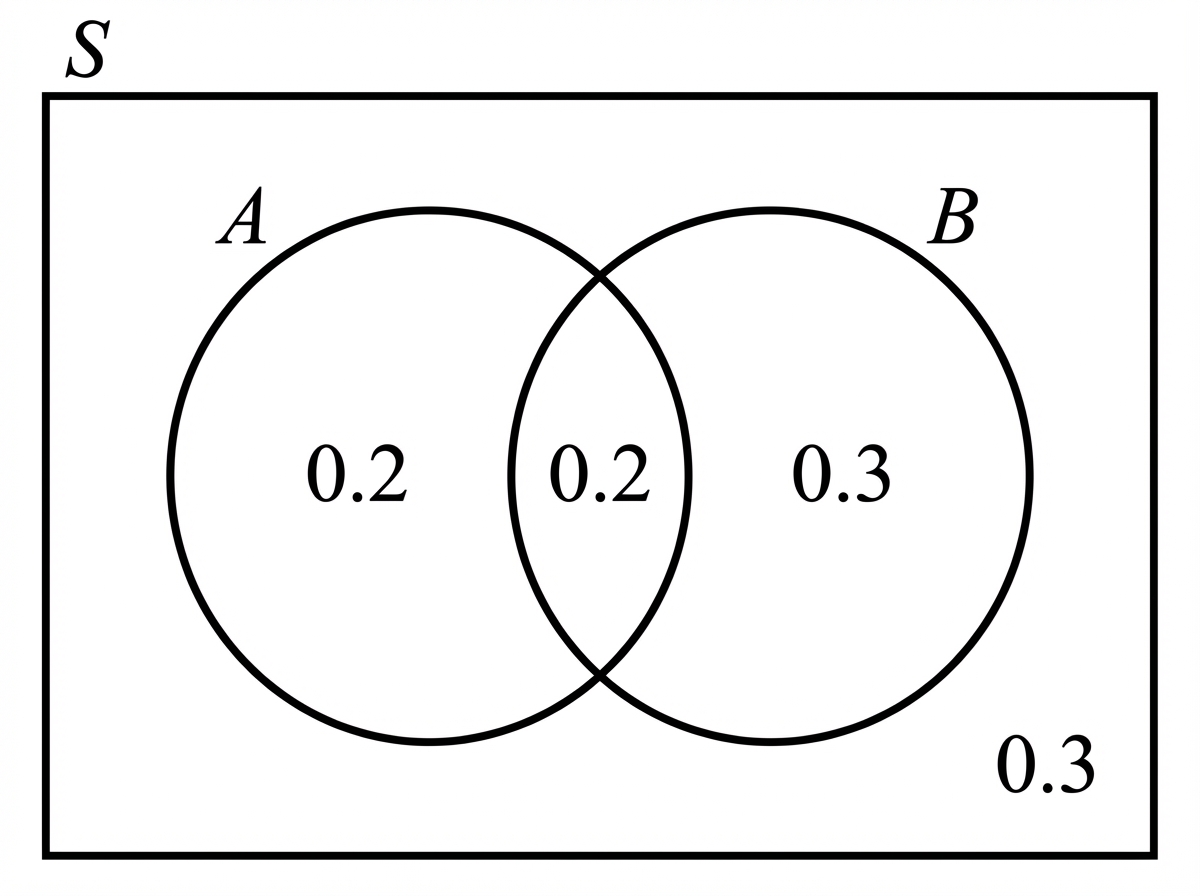
Calculate $P(A\cup B)$. [2 marks]

Three events $A$, $B$ and $C$ satisfy $P(A)=0.4$, $P(B)=0.5$, $P(C)=0.3$, $P(A\cap B)=0.1$, $P(A\cap C)=0.05$, $P(B\cap C)=0.07$ and $P(A\cap B\cap C)=0.02$.

Compute $P(A\cup B\cup C)$.

A test has a pass probability of $0.7$. If a candidate fails, they retake the test once, with the same pass probability.

Draw a tree diagram to represent this situation and find the probability that the candidate passes the test at least once.