Question Type 5: Applying adjacency matrices with some real world context Exercises

Compute the eigenvector centrality of node 1 in the $2 \times 2$ adjacency matrix $A = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}$ by finding the normalized eigenvector corresponding to the largest eigenvalue.

In a social network, the adjacency matrix $A$ (where $A_{ij}=1$ if users $i$ and $j$ are friends, and $0$ otherwise) is defined as:

$A = \begin{pmatrix} 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{pmatrix}$

Determine how many mutual friends users 1 and 2 share.

Use the adjacency matrix of the directed graph below to compute the reachability matrix (transitive closure).

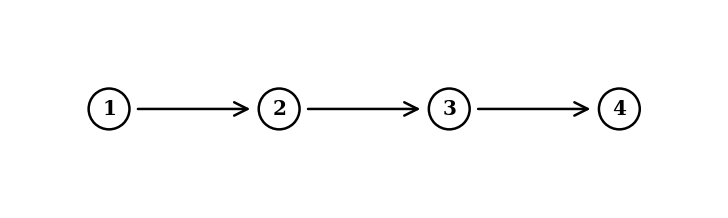
Label nodes in order 1 to 4.

Construct the adjacency matrix for a directed network of 4 nodes where the directed edges are: $1 \to 2$, $2 \to 3$, $3 \to 4$, $4 \to 1$, and $2 \to 4$.

A directed graph has adjacency matrix
$A = \begin{pmatrix} 0 & 1 & 1 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix}$ Compute the number of distinct paths of length 2 from vertex 1 to vertex 3.

The undirected graph $G$ has adjacency matrix:

$A = \begin{pmatrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\ \end{pmatrix}$

Find the degree of vertex 2 in $G$.

A transportation network of 3 cities has adjacency matrix

where $A_{ij} = 1$ if there is a direct bus route between city $i$ and city $j$. Find the number of different two-bus-ride itineraries that exist from city 1 to city 2 (allowing revisits).

In a social network with adjacency matrix $\mathbf{A}$ representing the friendships between 5 users, it is given that the entry $(\mathbf{A}^3)_{1,5} = 4$. Interpret this value in the context of the social network.

Given an undirected graph with adjacency matrix $A$, show that the trace of $A^3$ equals $6$ times the number of triangles in the graph.

Given the adjacency matrix of an undirected graph with 4 vertices:

$A = \begin{pmatrix} 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ \end{pmatrix}$

Determine the number of edges in the graph.

Calculate the number of distinct two-leg flight options from airport 1 to airport 3.

A social network’s adjacency matrix $A$ is given by

$A = \begin{pmatrix} 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 \end{pmatrix}$

Determine whether the network is bipartite.

The directed graph $G$, shown below, has vertices $V = \{1, 2, 3, 4\}$.

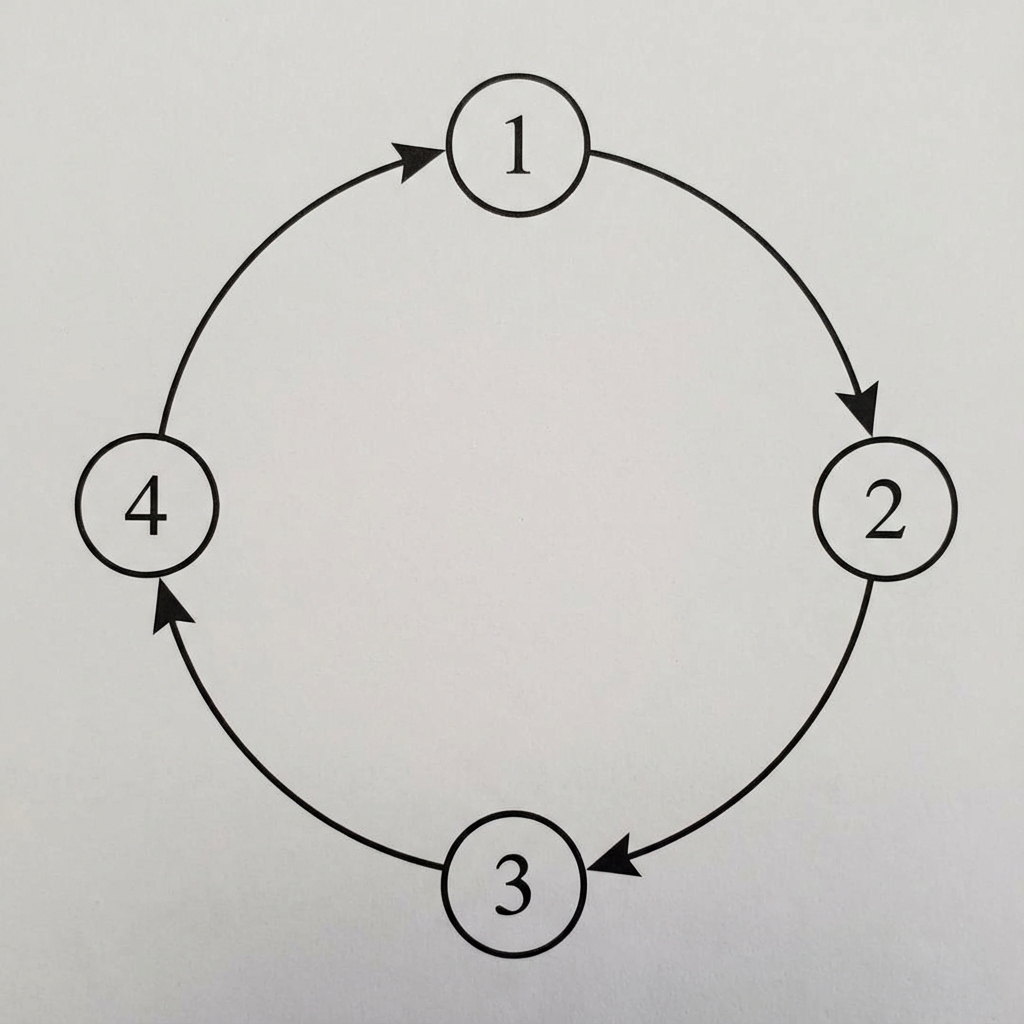
Determine whether the graph $G$ is strongly connected. Justify your answer.

A weighted adjacency matrix $W$ for 3 warehouses shows shipping times (in hours):

$W = \begin{pmatrix} 0 & 2 & 5 \\ 2 & 0 & 3 \\ 5 & 3 & 0 \end{pmatrix}$

Ignoring the weights, find how many distinct two-hop routes exist from warehouse 1 to warehouse 3.